繰り返し計測された連続データを適切に扱うために必要な線形混合モデル。
ランダム切片モデルが一番単純で有名だが、その切片はどんなふうになっているか。
通常の線形モデルの切片はどんな計算になっているか?
例えば、連続データ CDratio1 を 3 群のFCZで予測する線形モデルの場合、以下のような結果になる。

このときCDratio1の予測値 $ \hat{Y} $ は、以下の式で書ける。
$$ \hat{Y} = 160.10 + (-8.39) X_{FCZ 100-200} + (-2.35) X_{FCZ 400} $$
$ X_{FCZ 100-200} $、$ X_{FCZ 400} $ は、それぞれのカテゴリを表すダミー変数である。どちらもゼロの場合は、FCZ 0群を表す。
この式から、それぞれの群の予測値が、それぞれの群の平均値に一致していることが確認できる。
- FCZ 0: 160.10
- FCZ 100-200: 160.10 – 8.39 = 151.71
- FCZ 400: 160.10 – 2.34 = 157.76
各群の平均値の集計値は以下の通り同じである。
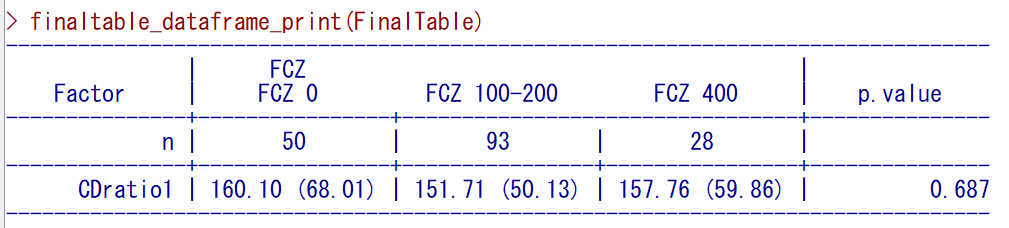
上記表内は、平均値(標準偏差)で集計値が表示されている。
線形混合モデルの切片はどんな計算になっているか?
では、繰り返し測定の線形混合モデルの場合、切片はどんな値になるのだろうか?
CDratioは、週ごとに3回の繰り返し測定した値で、それをFCZの3群で比較する線形混合モデルを考える。
3回の繰り返しは隔週なので、Weeksという変数にする。
線形混合モデルの解析結果は以下のとおりである。
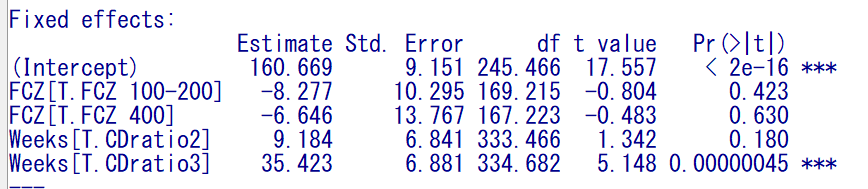
切片(Intercept)を見ると、160.669となっていて、線形モデルの 160.10 とは異なる。
FCZ のうち、FCZ 0は結果に登場してきていないカテゴリ。
Weeks のうち、CDratio1 が結果に登場してきていないカテゴリ。
基準カテゴリ FCZ 0 かつ CDratio1 の平均は、上記の計算では切片で、160.10 であった。
つまり、この計算結果の切片は 160.10 ではないのか?という疑問が生じるわけだ。
しかしそうではない。
これは3回繰り返し測定している各個人特有の切片、ランダム切片が加味されているからである。
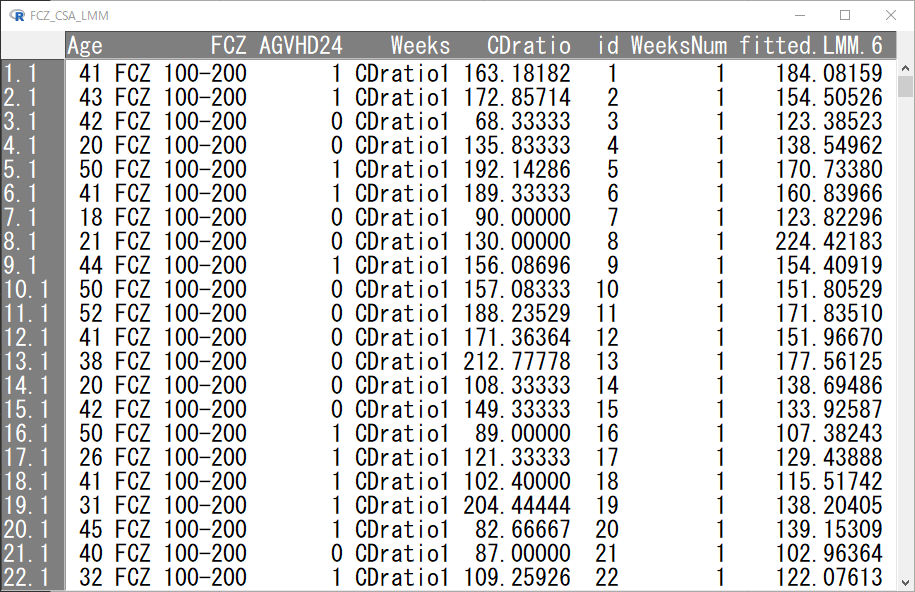
線形混合モデルの解析結果であるアクティブモデルを選択しておき、EZRの標準メニューのモデル→計算結果をデータとして保存 を使って、予測値を計算し、保存する。
fitted.LMM.X (今回の場合はXは6)という変数が増える。
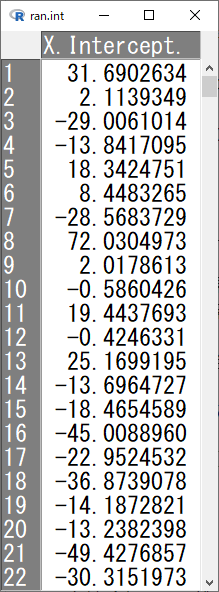
アクティブモデルにranef() 関数を実行する。
ranef(LMM.6)
これは被験者ごとの切片、すなわちランダム切片を出力してくれる。
WeeksがCDratio1のデータだけ残し、ランダム切片をcbindで結合して保存する。
1件、欠損値のせいか、ランダム切片が計算できていなかった症例があり、それは除いた。
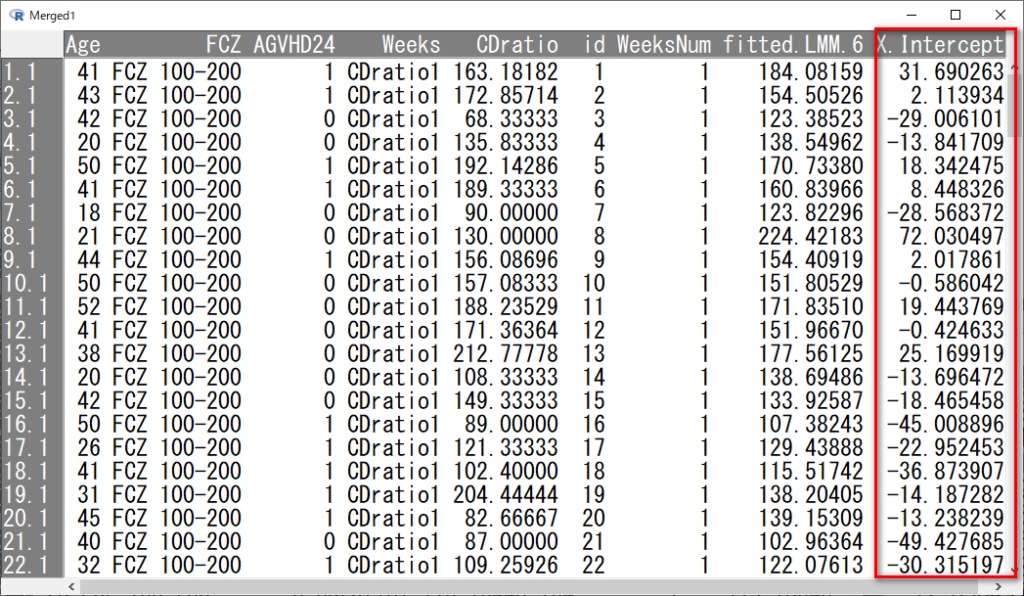
X.Intercept. がランダム切片(被験者ごとの切片)である。
最後に、FCZ 0群だけ残し、fitted.LMM.6 から X.Intercept. を引くと、すべて同じ160.6686と計算される。
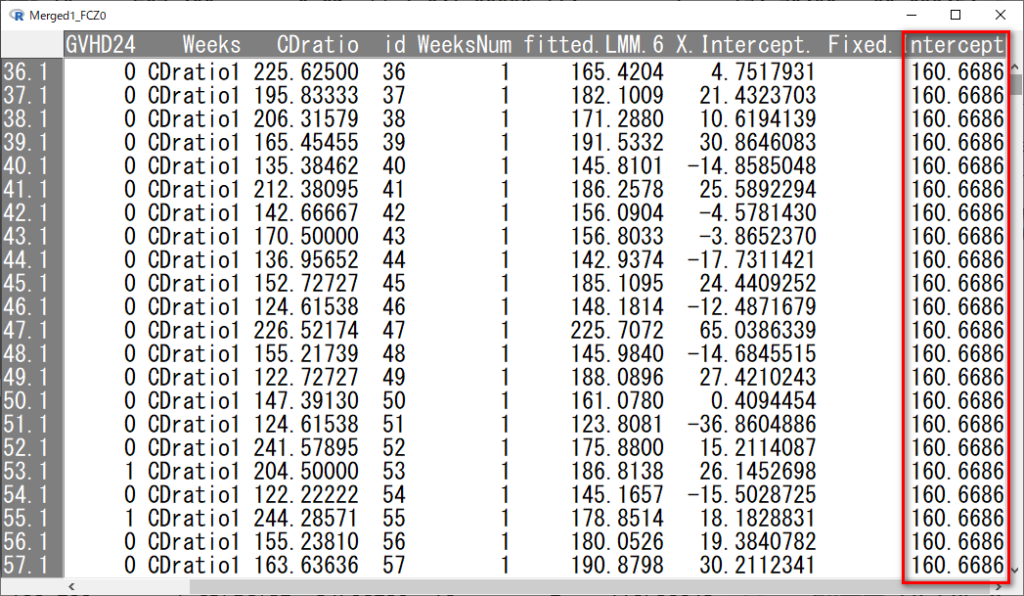
これが固定効果の切片 160.669である。
こういう関係性になっている。
なので、FCZ 0で、CDratio1という全体平均のグループであっても、一人ひとり別々の切片(ランダム切片)を持っていて、それが加味されているので、固定切片は FCZ 0 かつ CDratio1 の平均というわけではないということだ。
まとめ
線形混合モデルの切片について、ランダム切片の存在を明確にし、線形モデルの切片との比較をしながら、その違いについて紹介した。
参考サイト
おすすめ書籍
EZR公式マニュアル







コメント