因果推論の分野では、観察研究からバイアスの少ない効果を推定するために様々な手法が用いられる。その中でも、Inverse Probability of Treatment Weighting(IPTW)は、共変量の不均衡を調整し、治療群と対照群を「比較可能」にする強力なツールである。IPTWを適用した後に回帰モデルを構築することはよく行われるが、この際に多くの研究者が見落としがちな、しかし極めて重要な側面がある。それが適切な標準誤差の推定である。本記事では、IPTWを用いた回帰モデルにおける標準誤差の重要性と、その適切な計算方法について掘り下げる。
IPTW回帰分析概要
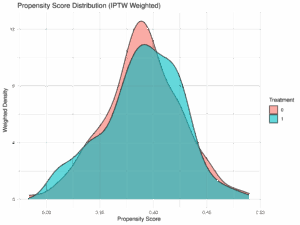
IPTWは、各個人の治療割り付け確率の逆数を用いて重み付けを行う手法である。これにより、観察データにおける共変量の分布を平衡させ、あたかもランダム化比較試験(RCT)のように治療群と対照群を比較できる状態を作り出す。
IPTWを適用した後、通常は以下のような重み付き回帰モデルを構築する。
$$Y_i = \beta_0 + \beta_1 T_i + \beta_2 X_i + \epsilon_i$$
ここで、$Y_i$はアウトカム、$T_i$は治療割り付け(0または1)、$X_i$は共変量、$\epsilon_i$は誤差項である。そして、この回帰モデルはIPTWによって計算された重み$w_i$を用いて推定される。
適切な標準誤差計算の必要性
IPTWを用いた回帰モデルにおいて、単純にOLS(最小二乗法)の標準誤差をそのまま用いることは誤りである。その理由は以下の2点に集約される。
- 重みの推定誤差: IPTWで用いられる重みは、プロペンシティスコア(治療割り付け確率)を推定することによって得られる。このプロペンシティスコアの推定には統計的な誤差が含まれており、この誤差は最終的な回帰モデルのパラメータ推定値の不確実性に影響を与える。しかし、標準的な回帰分析の標準誤差は、この重みの推定誤差を考慮していない。
- 異なった分散構造: IPTWによって重み付けされたデータは、元のデータとは異なる分散構造を持つ可能性がある。特に、極端な重みが存在する場合には、それが標準誤差に大きな影響を与えることがある。
これらの理由から、一般的な統計ソフトウェアがデフォルトで出力する標準誤差は、IPTWを用いた回帰モデルにおいては過小評価される傾向があり、結果として信頼区間が狭くなり、統計的に有意ではないはずの治療効果が有意であると誤って判断されるリスクがある。これは、研究結果の信頼性を著しく損なうことにつながる。
適切な標準誤差を推定するためには、主に以下の手法が用いられる。
- ロバスト標準誤差(Robust Standard Errors / Huber-White Standard Errors): これは、異なった分散構造に対応できる標準誤差の推定方法である。重み付けされたデータに対しても適用可能であり、ある程度の頑健性を提供する。
- ブートストラップ法(Bootstrap): データから反復的にリサンプリングを行うことで、パラメータ推定量の標本分布を経験的に推定し、そこから標準誤差を計算する方法である。重みの推定過程も考慮に入れることができるため、より正確な標準誤差を提供する。
- サンドイッチ分散推定器(Sandwich Variance Estimator): 特にプロペンシティスコアの推定を考慮したより洗練された方法である。
具体例とR計算例
ここでは、架空のデータを用いて、RでのIPTW回帰と標準誤差の計算例を示す。
# 必要なライブラリのインストールと読み込み (初回のみ)
# install.packages("cobalt")
# install.packages("WeightIt")
# install.packages("survey")
library(cobalt) # バランスチェック用
library(WeightIt) # IPTW重み計算用
library(survey) # 調査データ分析用(ロバスト標準誤差計算に便利)
# データの生成 (仮想データ)
set.seed(123)
n <- 1000
# まずXとTを生成
X <- rnorm(n)
T <- rbinom(n, 1, plogis(0.5 * X))
# 次にYを生成(TとXに依存)
Y <- 0.5 * T + 0.3 * X + rnorm(n, sd = 2)
# データフレームにまとめる
data <- data.frame(X = X, T = T, Y = Y)
# 1. プロペンシティスコアの推定とIPTW重みの計算
# TをYに、Xを共変量として、二項ロジスティック回帰でプロペンシティスコアを推定
# WeightItパッケージを使用
w.out <- weightit(T ~ X, data = data, method = "glm", estimand = "ATE")
# 重みの取得
data$weights <- w.out$weights
# 重み付け後の共変量のバランスチェック (オプション)
bal.tab(w.out, stats = c("m", "v"))
# 2. IPTW重みを用いた回帰モデルの構築
# 通常のlm関数を用いた回帰モデル (標準誤差が不適切)
# この標準誤差は重みの推定誤差を考慮していないため、過小評価される可能性が高い
fit_lm <- lm(Y ~ T + X, data = data, weights = weights)
summary(fit_lm)
# 3. 適切な標準誤差の計算
# 方法1: surveyパッケージを用いたロバスト標準誤差
# surveyデザインオブジェクトを作成
# id = ~1 はクラスタリングがないことを示す
# weights = ~weights はIPTW重みを指定
# data = data は使用するデータフレーム
design_obj <- svydesign(id = ~1, weights = ~weights, data = data)
# surveyパッケージのsvyglm関数で回帰モデルを推定
# family = gaussian() は連続アウトカムの場合
fit_svyglm <- svyglm(Y ~ T + X, design = design_obj, family = gaussian())
summary(fit_svyglm)
# 方法2: ブートストラップ法 (例)
# より計算コストがかかるが、より正確な標準誤差を提供することがある
# ここでは簡単な例を示すが、実際にはプロペンシティスコアの推定から含めてブートストラップを行う
# bootパッケージなどを用いるとより簡単に実装できる
# ブートストラップ関数の定義
bootstrap_fn <- function(data, indices) {
d_boot <- data[indices, ]
# ブートストラップサンプルでプロペンシティスコアと重みを再計算
w.out_boot <- weightit(T ~ X, data = d_boot, method = "glm", estimand = "ATE")
d_boot$weights <- w.out_boot$weights
# 重み付き回帰モデルの推定
fit_boot <- lm(Y ~ T + X, data = d_boot, weights = weights)
coef(fit_boot)["T"] # Tの係数を返す
}
# ブートストラップの実行
library(boot)
boot_results <- boot(data = data, statistic = bootstrap_fn, R = 1000)
# Tの係数のブートストラップ標準誤差
sd(boot_results$t)
# 95%信頼区間
boot.ci(boot_results, type = "perc", index = 1)
実行結果:
> # この標準誤差は重みの推定誤差を考慮していないため、過小評価される可能性が高い
> fit_lm <- lm(Y ~ T + X, data = data, weights = weights)
> summary(fit_lm)
Call:
lm(formula = Y ~ T + X, data = data, weights = weights)
Weighted Residuals:
Min 1Q Median 3Q Max
-8.4323 -1.9183 0.0264 1.8326 10.3289
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0008543 0.0897755 0.010 0.99241
T 0.3809942 0.1268489 3.004 0.00274 **
X 0.3091287 0.0637750 4.847 1.45e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.836 on 997 degrees of freedom
Multiple R-squared: 0.03166, Adjusted R-squared: 0.02972
F-statistic: 16.3 on 2 and 997 DF, p-value: 1.085e-07
>
> # 方法1: surveyパッケージを用いたロバスト標準誤差
> summary(fit_svyglm)
Call:
svyglm(formula = Y ~ T + X, design = design_obj, family = gaussian())
Survey design:
svydesign(id = ~1, weights = ~weights, data = data)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0008543 0.0855744 0.010 0.99204
T 0.3809942 0.1305390 2.919 0.00359 **
X 0.3091287 0.0638416 4.842 1.49e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for gaussian family taken to be 4.014566)
Number of Fisher Scoring iterations: 2
>
> # 方法2: ブートストラップ法 (例)
> # より計算コストがかかるが、より正確な標準誤差を提供することがある
> # Tの係数のブートストラップ標準誤差
> sd(boot_results$t)
[1] 0.1392221
> # 95%信頼区間
> boot.ci(boot_results, type = "perc", index = 1)
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates
CALL :
boot.ci(boot.out = boot_results, type = "perc", index = 1)
Intervals :
Level Percentile
95% ( 0.1067, 0.6557 )
Calculations and Intervals on Original Scale
> 上記のRコード例では、lm関数を用いた場合の標準誤差(0.127)と、surveyパッケージのsvyglmを用いた場合のロバスト標準誤差(0.131)の違いが確認できる。svyglmを用いた方が、一般的に標準誤差が大きくなる傾向がある。ブートストラップはより計算量が多いが、プロペンシティスコアの推定誤差まで考慮した標準誤差(0.139)を計算できる。
結果解釈例
IPTWを用いた回帰モデルの結果を解釈する際には、推定された治療効果の係数($\beta_1$)だけでなく、その標準誤差とそれに基づいて計算されたp値、そして信頼区間を総合的に考慮する必要がある。
例えば、上記のsvyglmの結果で、治療効果(Tの係数)が0.381、標準誤差が0.131であった。この場合、95%信頼区間はおおよそ$[0.381 – 1.96 \times 0.131, 0.381 + 1.96 \times 0.131] = [0.124, 0.638]$ となる。
もし不適切な標準誤差(例えば0.127)を用いていた場合、信頼区間は$[0.381 – 1.96 \times 0.127, 0.381 + 1.96 \times 0.127] = [0.132, 0.630]$ となり、より狭い区間が算出されてしまう。これにより、本来は統計的有意性がない可能性のある効果が、過剰に有意であると解釈されるリスクが生じる。
適切な標準誤差を用いることで、推定された治療効果が偶然によるものではないか、あるいはその効果の不確実性がどの程度大きいのかをより正確に把握することができる。これは、研究結果の頑健性と信頼性を確保するために不可欠である。
まとめ
IPTWを用いた回帰モデルは、観察研究における因果効果の推定に非常に強力なツールである。しかし、その力を最大限に引き出し、誤った結論を導かないためには、標準誤差の適切な推定が不可欠である。プロペンシティスコアの推定誤差やデータ構造の変更を考慮しない標準誤差は、分析結果の信頼性を損なう可能性がある。
ロバスト標準誤差やブートストラップ法などの適切な手法を用いて標準誤差を計算することで、より正確で信頼性の高い因果効果の推定が可能となる。研究者としては、これらの重要な側面を理解し、分析に適切に組み込むことで、より質の高い研究成果を生み出すことができるだろう。





コメント