臨床研究では、比較的まれな疾患の患者さんのデータと、その疾患を持たない対照群のデータを比較しようとすると、両グループの人数が大きく異なることがよくある。これは、まれな疾患ではそもそもデータが集まりにくいという現実があるためだ。
このように、人数の少ないグループと人数の多いグループを統計的に比較することに問題はないのか、という疑問が生じるのは当然である。本稿では、この問題に対する考え方と、実際のデータ解析における注意点について解説する。
サンプル数が大きく異なる群間比較の状況
臨床現場では、比較的まれな疾患、特にその非定型例に遭遇することは少なくない。
臨床研究のサンプル数を検討する際、定型例が10,000例に対して非定型例が100例のように、サンプル数に大きな開きが出ることがある。
このような状況で、サンプル数が大きく異なる二群間をそのままStudentのt検定、Welchのt検定、あるいはMann-Whitney U検定などで比較して良いのか、という疑問が生じるのは当然である。
非定型例100例に見合うサンプルを定型例から抽出して比較すべきだという意見もあるだろう。
サンプル数が大きく異なる群間比較に関する考察
サンプル数が大きく異なる群間比較に懸念を抱く気持ちは理解できる。
これはおそらく、群間のサンプル数が不均衡だと、統計的な有意差が出にくくなるという認識があるためかもしれない。
実際、全体のサンプル数が固定されている場合、各群のサンプル数が1対1でバランスしているときに統計学的検出力は最大になる。
しかし、症例集積の努力によって全体のサンプル数を大きくできるのであれば話は別だ。
例えば、非定型例100例に合わせて定型例も100例に絞り込んでしまうと、全体のサンプル数が小さくなるため、結果として統計学的検出力は低下してしまう可能性がある。
つまり、1対1というバランスは確かに理想的ではあるが、それによって全体のサンプル数が小さくなり、検出力が下がってしまうのは本末転倒と言える。
無理にサンプル数を合わせることで、せっかく得られた多くの情報が無駄になり、本来検出できるはずの差を見逃す可能性が高まることがある。
サンプル数が異なる2群の連続データを比較する場合の検出力
2群の差が中程度の場合(例えば、平均値の差を標準偏差で標準化したときに0.5程度)を考える。
EZRを用いた計算方法で、検出力がどのように変化するかを見てみる。
「統計解析」→「必要サンプルサイズの計算」→「2群の平均値の比較のためのサンプルサイズの計算」を選択し、以下の数値を入力する。
- 2群間の平均値の差:0.5
- 2群共通の標準偏差:1
- その他:デフォルト設定
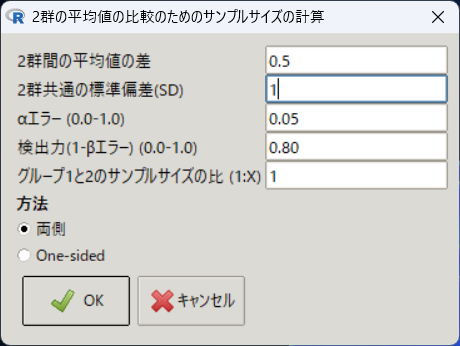
この設定で計算すると、1群あたり63例が必要と計算される。
> SampleMean(0.5, 1, 0.05, 0.80, 2, 1)
仮定
2群間の平均値の差 0.5
標準偏差 1
αエラー 0.05
両側検定
検出力 0.8
N2とN1のサンプルサイズの比 1
必要サンプルサイズ 計算結果
N1 63
N2 63このとき、2群合わせると126例となる。
この合計サンプルサイズのまま、2群のサンプルサイズ比を変えた場合の検出力を見てみる。
検出力は、検定によって統計学的有意な差を検出する力であり、一般的に80%を超えていることが望ましいとされている。
検出力を計算するには、「統計解析」→「必要サンプルサイズの計算」→「2群の平均値の比較のための検出力の計算」を用いる。
平均値の差を0.5、標準偏差を1、両群のサンプルサイズを63とすると、検出力は約80%と計算される。
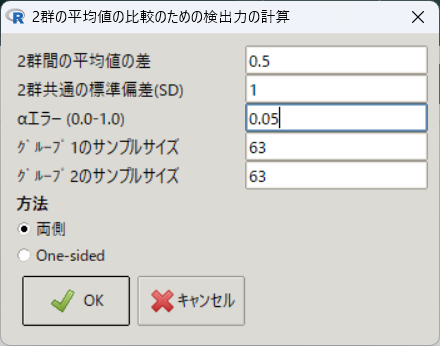
> PowerMean(0.5, 1, 0.05, 63, 2, 1)
仮定
2群間の平均値の差 0.5
標準偏差 1
αエラー 0.05
両側検定
サンプルサイズ
N1 63
N2 63
計算結果
検出力 0.801ここで、合計126例の振り分けを1:2、つまり42例と84例とすると、検出力は約75%に下がる。
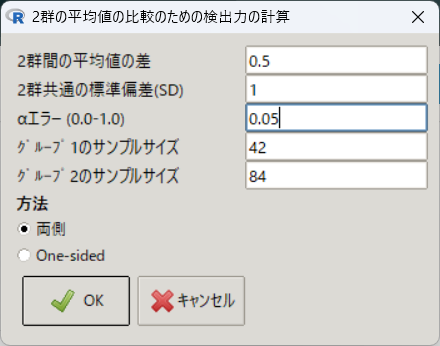
> PowerMean(0.5, 1, 0.05, 42, 2, 2)
仮定
2群間の平均値の差 0.5
標準偏差 1
αエラー 0.05
両側検定
サンプルサイズ
N1 42
N2 84
計算結果
検出力 0.7541:4程度にして、26例と100例とすると、検出力は約62%にまで落ち込む。
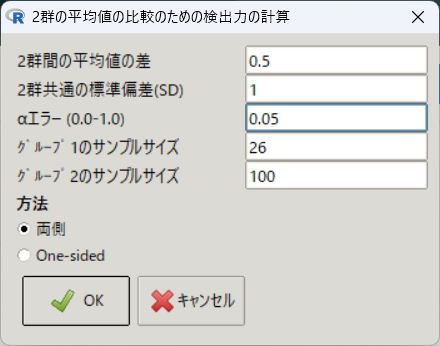
> PowerMean(0.5, 1, 0.05, 26, 2, 3.84615384615385)
仮定
2群間の平均値の差 0.5
標準偏差 1
αエラー 0.05
両側検定
サンプルサイズ
N1 26
N2 100
計算結果
検出力 0.622さらに1:10(12例と114例)にしてみると、検出力は約38%を下回ってしまう。
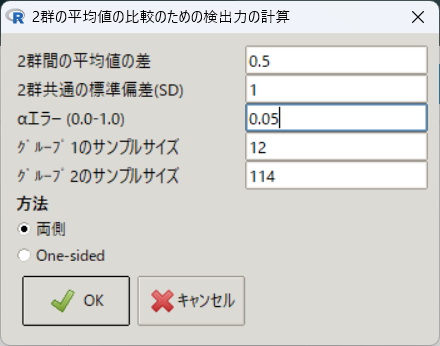
> PowerMean(0.5, 1, 0.05, 12, 2, 9.5)
仮定
2群間の平均値の差 0.5
標準偏差 1
αエラー 0.05
両側検定
サンプルサイズ
N1 12
N2 114
計算結果
検出力 0.377この計算結果から、合計のサンプルサイズが同じという条件では、2群のサンプルサイズが大きく異なると検出力が低下し、適切な比較が難しくなることがわかる。
全体のサンプル数を増やすことの重要性
それでは、どのようにすればよいのだろうか。
解決策は、全体のサンプルサイズを増やすことにある。
例えば、1:1の比率で検出力80%を達成するためには63例ずつ(合計126例)必要だった。
これを1:2の比率で検出力80%を維持したい場合、合計のサンプルサイズを18例増やし、合計144例(48例+96例)とすれば達成可能である。
> SampleMean(0.5, 1, 0.05, 0.80, 2, 2)
仮定
2群間の平均値の差 0.5
標準偏差 1
αエラー 0.05
両側検定
検出力 0.8
N2とN1のサンプルサイズの比 2
必要サンプルサイズ 計算結果
N1 48
N2 961:4の比率では、合計200例に増やすことで検出力80%を維持できる。
> SampleMean(0.5, 1, 0.05, 0.80, 2, 4)
仮定
2群間の平均値の差 0.5
標準偏差 1
αエラー 0.05
両側検定
検出力 0.8
N2とN1のサンプルサイズの比 4
必要サンプルサイズ 計算結果
N1 40
N2 160さらに極端な1:10の比率でも、合計385例であれば検出力80%を維持できる。
> SampleMean(0.5, 1, 0.05, 0.80, 2, 10)
仮定
2群間の平均値の差 0.5
標準偏差 1
αエラー 0.05
両側検定
検出力 0.8
N2とN1のサンプルサイズの比 10
必要サンプルサイズ 計算結果
N1 35
N2 350つまり、もし2群のサンプルサイズが大きく異なっていても、十分な合計サンプルサイズがあれば、統計学的検出力を維持することは可能である。
わざわざ少ない方の群に合わせて全体のサンプルサイズを小さくする必要はない。
可能な限り多くのデータを用いることが望ましいと言える。
片群のサンプル数が少ないケースコントロール研究におけるマッチングについて
片群(ケース)のサンプル数が少ないケースコントロール研究において、コントロールが豊富にある場合にどうすべきかという疑問はよくある。
結論としては、利用可能なデータはすべて活用し、無理にマッチングをしない方がより適切である場合が多いと考えられる。
マッチングの限界
ケース数が少なくコントロールが潤沢にある場合、1:nのマッチング、例えば1:100のようなマッチングを検討することもあるかもしれない。
しかし、マッチングによって検出力(統計的に有意な差を見つける能力)が向上するのは、概ね1:5程度までであるとされている。
それ以上のコントロール数を増やしても、統計的な検出力はほとんど上がらないため、多くのコントロールをマッチングする作業は、労力の割に得られるメリットが少ない可能性がある。
例えば、喫煙と肺がんの関係を調べるケースコントロール研究で、肺がん患者(ケース)が100人しかいないが、非喫煙者(コントロール)は10,000人いるとする。
このとき、1:100でマッチングを行い、ケース100人に対してコントロール10,000人の中から100人を選び出すことは、一見バランスが取れているように思えるかもしれない。
しかし、この場合、多くの情報を捨てていることになり、データが持つ潜在的な情報を十分に活用できていない可能性がある。
すべてのデータを活用する利点
一方で、ケース100例とコントロール10,000例が同等の質でデータが取得されているのであれば、無理にサンプル数を絞らずに、そのまま解析を進めるのが最も妥当なアプローチの一つである。
サンプル数を意図的に減らすような操作は、データの持つ情報を不必要に捨てることになり、統計的な効率を低下させることにつながる。
例として、ある希少疾患のリスク因子を調べる研究を考える。
その疾患の患者(ケース)が全国で100人しか特定できなかったとしても、健康な人(コントロール)は容易に10,000人集められたとする。
この場合、疾患患者100人と健常者10,000人というサンプルサイズで、そのまま解析を進めることが可能です。
わざわざ健常者のデータを9,900人分捨てて100人に絞り込む必要性は低い。
利用可能なデータは最大限に活用することで、より信頼性の高い結果を得られる可能性が高まる。
したがって、片群のサンプル数が少ないケースコントロール研究においては、マッチングに固執せず、利用可能なすべてのデータを解析に投入することを検討することが推奨される。
ただし、データ量が多い場合は、計算負荷や解析手法の選択に配慮が必要となることもある。
サンプル数が異なる群間比較の留意点
しかしながら、サンプルサイズが大きく異なる群間比較を行う際には、いくつかの重要な点に留意する必要がある。
データ分析の信頼性と結果の適切な解釈のために、特に以下の統計的・臨床的側面に留意する必要がある。
ケースコントロール研究におけるモデル選択とサンプルサイズ不均衡の影響
ケースコントロール研究では、単純な二群間の比較に留まらず、回帰モデルや予測モデルを構築して、より多角的に疾患と関連因子を解析することが一般的である。
しかし、この際にサンプルサイズの大きな不均衡を考慮しないと、モデルの性能や解釈に深刻な影響を及ぼす可能性がある。
サンプルサイズ不均衡がモデルに与える影響
サンプルサイズが著しく異なる場合、特に少数群(ケース)のデータが不足していると、以下のような問題が生じやすくなる。
- モデルの推定精度の低下: 多数群のデータに引っ張られ、少数群における特徴や関連性が適切にモデル化されにくくなる。これにより、特に少数群において重要な因子が見過ごされたり、関連性の強度が過小評価されたりするリスクがある。
- 予測性能の偏り: 構築されたモデルが、多数派であるコントロール群の予測には優れていても、希少なケース群の予測精度が低くなることがある。これは、モデルが多数派のパターンを学習することに最適化されるためである。
- 過学習(Overfitting)のリスク: 少数群のデータが極端に少ない場合、モデルが少数群のわずかな特徴に過剰に適合してしまい、未知のデータに対する汎化性能が低下する可能性がある。
具体例: まれな疾患の発症リスク予測モデル
あるまれな疾患の発症リスクを予測するモデルを、患者100人と健常者10,000人のデータで構築するケースを考える。
- もし、モデルが「患者群に特有の小さなバイオマーカーの変化」を捉えるべきであるにもかかわらず、その変化が100人のデータでは非常に小さく、かつ10,000人の健常者のデータの中に埋もれてしまう場合、モデルはこの重要な因子を適切に検出できないかもしれない。
- 結果として、構築されたモデルは健常者を「健常である」と高い精度で予測できる一方で、実際に疾患を発症する患者を「患者である」と予測する精度が著しく低い、という事態に陥る可能性がある。これは、臨床現場で真に役立つ予測モデルとは言えない。
対策とモデル構築時の考慮事項
このような不均衡の影響を緩和し、頑健なモデルを構築するためには、いくつかの対策が考えられる。
- 不均衡データ対応の統計手法の利用:
- サンプリング手法: 多数群からランダムに抽出して少数群とバランスを取るアンダーサンプリング、または少数群のデータを人工的に増やすオーバーサンプリング などがある。これにより、モデル学習時のクラス比率を調整し、モデルが少数クラスをより重視するように促す。
- コスト感度学習: 誤分類のコストをクラス間で異ならせることで、少数クラスの誤分類に対してより大きなペナルティを与える手法。
- 適切なモデル評価指標の選択: 単純な正解率(Accuracy) だけでなく、感度(Sensitivity/Recall)、特異度(Specificity)、適合率(Precision)、F1スコア、そしてROC曲線下の面積(AUC) など、少数クラスの予測性能を適切に評価できる指標を用いるとよい。
- モデルの調整と検証: 多変量解析の枠組みにおいて、交絡因子を適切に調整する変数選択を行うとともに、モデルの内部妥当性(internal validity) と外部妥当性(external validity) を慎重に検証する必要がある。特に不均衡データでは、交差検証(cross-validation)などの手法を適切に適用し、過学習を防ぐことが重要である。
マッチングの有効性と適用場面
サンプルサイズが大きく異なる群間比較において、マッチングは非常に有効なデータ調整手法となり得る。
特に、実データを用いた研究では、1:1のマッチングが強力な効果をもたらす場面が少なくない。
問題点の概要:複雑な交絡とモデルベース調整の限界
多変量解析、特に回帰モデルを用いた交絡調整は強力なツールであるが、以下のような状況ではその適用に限界が生じることがある。
- 交絡の複雑性: 複数の交絡因子が複雑に絡み合い、その関係性が非線形であったり、交互作用が存在したりする場合、単純な回帰モデルでは適切に調整しきれないことがある。
- モデルの特定化誤差: 使用する統計モデルがデータの真の関係性を正確に表現できていない場合(モデルの誤特定)、交絡調整が不十分となり、バイアスが残存する可能性がある。
- データ分布の不均衡: サンプルサイズが極端に異なる場合、多数群のデータが回帰モデルの推定に強く影響を与え、少数群における交絡因子の分布の偏りを十分に補正できないことがある。これにより、少数群における比較可能性の確保が難しくなる。
このような状況では、単に統計的な手法で交絡を調整するだけでは不十分であり、研究デザインの段階で比較可能性を確保するアプローチがより優先される場合がある。
具体例:喫煙と特定疾患のリスク研究
例えば、喫煙が特定の希少疾患(ケース)のリスクに与える影響を調べるケースコントロール研究を考えてみる。
患者群は100人、対照群は10,000人いるとする。
この場合、喫煙習慣だけでなく、年齢、性別、飲酒習慣、社会経済状況、他の併存疾患など、多数の因子が疾患リスクと喫煙習慣の両方に関連している可能性がある。
- 回帰モデルの限界: 仮に、喫煙習慣と疾患の関連が年齢や社会経済状況と複雑な交互作用を持つ場合、これらのすべての交絡因子を正確にモデルに組み込み、調整することは困難である。
- マッチングの有効性: ここで、ケース(患者)100人に対して、対照群10,000人の中から年齢、性別、飲酒習慣、社会経済状況などを類似させた100人(あるいは数人ずつ)をマッチングしたとする。これにより、喫煙以外の交絡因子を両群でバランスさせ、喫煙と疾患の関連性をより純粋に評価できる可能性が高まる。この1:1マッチングが、モデルベースの調整よりも強力な比較可能性をもたらすことがある。
対策案:マッチングの戦略的適用
上記の課題を踏まえ、以下のような対策案が考えられる。
- プロペンシティスコアマッチング(Propensity Score Matching: PSM)の活用:
- 多数の交絡因子が存在する場合に特に有効な手法である。各被験者が特定の曝露(例:疾患)を受ける確率(プロペンシティスコア)を算出し、そのスコアに基づいてケースとコントロールをマッチングする。
- 層化解析やサブグループ解析との組み合わせ: マッチングが困難な場合でも、主要な交絡因子でデータを層化し、各層内で比較を行うことで、交絡の影響をある程度制御できる。また、特定のサブグループにおいて、より強い関連性や異なる効果が観察される可能性を探ることも重要である。
まとめ
観察研究において、サンプルサイズが大きく異なる群間比較やケースコントロール比較を行うことは、適切な考慮のもとであれば問題ない。
つまり、取得したデータのうち、目的とする症例数が少ないからといって、少ない症例数に合わせた操作(マッチング等)を無理に行う必要は必ずしもない。
むしろ、可能な限り多くのデータを使うことで、統計学的検出力を高め、より信頼性の高い結果を得られる可能性が高まる。
ただし、サンプルサイズが大きく異なる場合でも、解析手法の選択や結果の解釈には慎重さが求められる。
例えば、統計モデルの仮定が満たされているか、共変量による調整が適切に行われているかなど、詳細な検討が必要である。
場合によっては、マッチングのほうが適切な場合があり、慎重な判断、必要に応じて、統計の専門家への相談が必要となるだろう。








コメント