EZR で Jonckheere-Terpstra 検定を行う方法

Jonckheere-Terpstra 検定（ヨンクヒール タプストラ検定、ヨンキー検定）とは？

Jonckheere-Terpstra検定とは？

３群以上の群で、単調に増加するか、単調に減少するかなどの傾向を検定するノンパラメトリックな検定法。

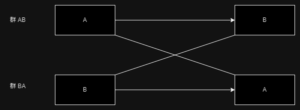
Jonckheere-Terpstra 検定は、データから計算される検定統計量の一部（Jと記載されることが多い）を、下の群の値と上の群の値一つ一つを比べて、下の群のほうが大きければゼロ、同じ場合は1/2、上の群のほうが大きければ１とスコアを付けて、それを全部足し合わせて計算する。

わかりやすい計算例は、下記リンク先PDF３枚目（p.37）。

https://www.lexjansen.com/pharmasug/1997/STAT_PK/st04.pdf

この計算は、マンホイットニーのU検定のUの計算方法に似ている。

マンホイットニーのU検定の実際の計算については、以下を参照。

実は、極端な話、群のnが１でも計算できる。

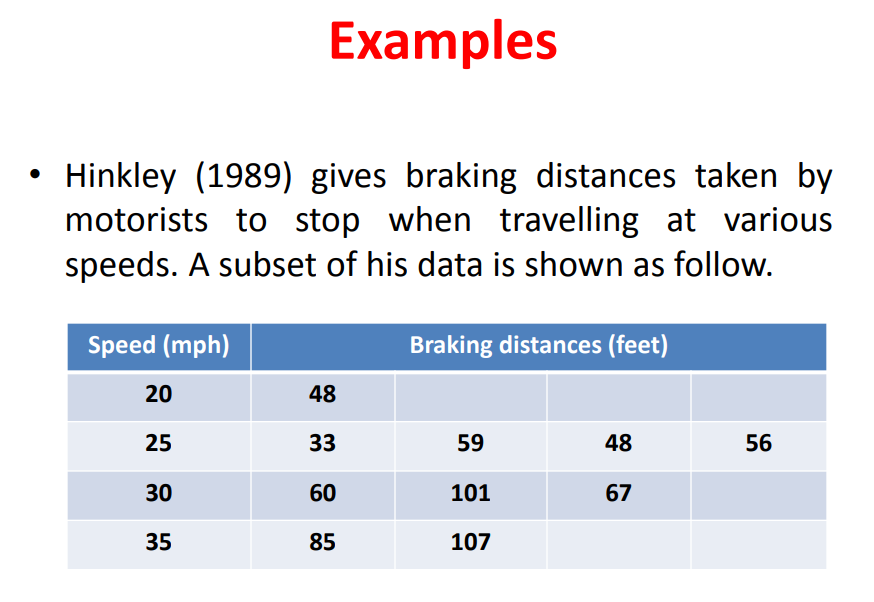
下記リンク先のスライド５枚目を見るとSpeed 20の群がn=1であるが、そのまま計算して結果が出ている。

https://pdfs.semanticscholar.org/7568/47d6034ee27737f2dce6015c94fda9be4597.pdf

Jonckheere-Terpstra検定はEZRではどうやるか？

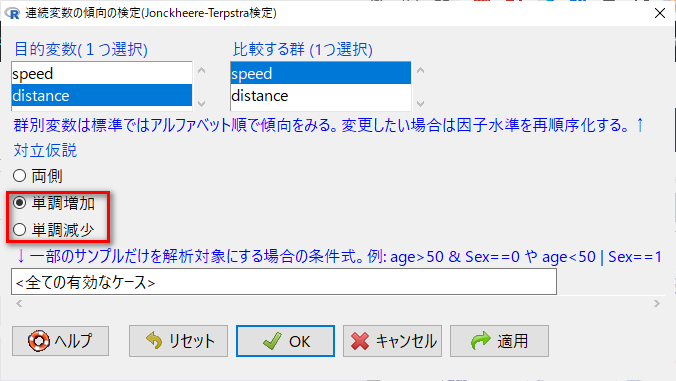
EZRでは、「統計解析」→「ノンパラメトリック検定」と進むと、Jonckheere-Terpstra検定が見つかる。

目的変数と説明変数（比較する群）を選択し、単調増加か単調減少かを選んで検定する。

上記でも紹介したサンプルデータで実際に計算してみる。

https://pdfs.semanticscholar.org/7568/47d6034ee27737f2dce6015c94fda9be4597.pdf

speed <- c(20,rep(25,4),rep(30,3), 35, 35)
distance <- c(48, 33, 59, 48, 56, 60, 101, 67, 85, 107)

speedグループの値の傾向性を無視して、Kruskal-Wallis検定を行うと以下の通りになる。

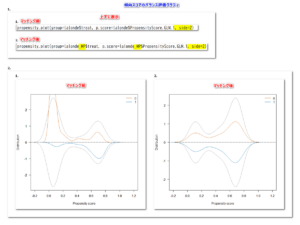
Jonckheere-Terpstra検定を行い、speedグループが大きくなると、単調に増加するという仮説を検定すると以下のようになる。

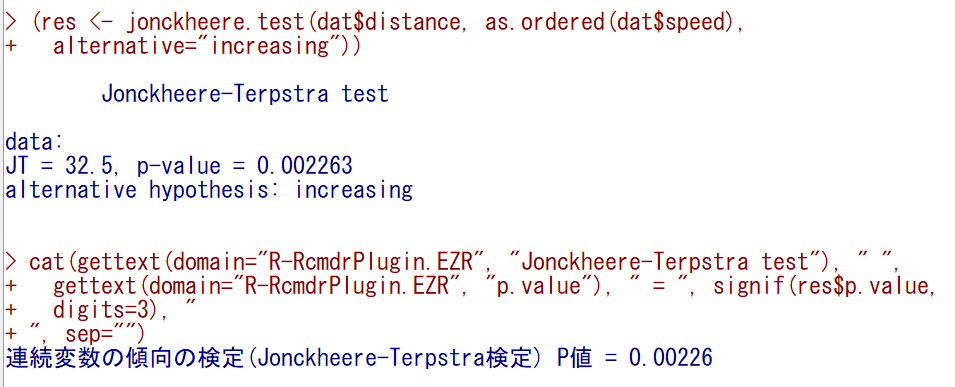
こちらであれば、統計学的に有意である。

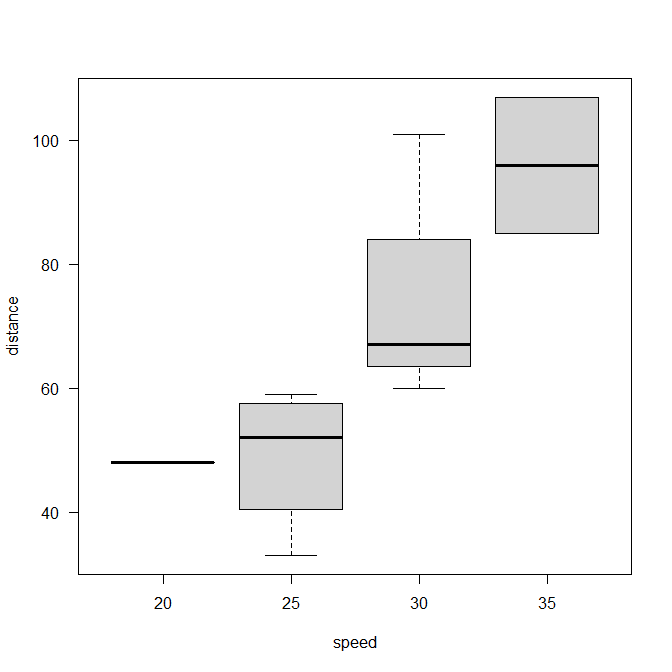
箱ひげ図を見ても明らかに単調増加しているので、Jonckheere-Terpstra検定のほうが適切と言える。

まとめ

Jonckheere-Terpstra 検定（ヨンクヒール タプストラ検定、ヨンキー検定）とは何か、どのように計算しているのか、EZRではどのように実施するのかについて紹介した。

原理的にも、実際的にも、n=1の群があっても使える。

参考になれば。

参考サイト

https://www.lexjansen.com/pharmasug/1997/STAT_PK/st04.pdf

https://pdfs.semanticscholar.org/7568/47d6034ee27737f2dce6015c94fda9be4597.pdf

参考書籍

EZR公式マニュアル