R でケンドールの順位相関係数を計算する方法

ケンドールの順位相関係数はどのように計算するか紹介する

ケンドールの順位相関係数

ケンドール（Kendall）の順位相関係数 $ \tau $ は、順位を使わない相関係数である。

何を使うかというと、値の大小を使う。

変数Xと変数Yの相関を計算する際に、2つのX,Yペアを取り出す。

片方のペアが、もう片方のペアより、XもYも大きい、もしくはXもYも小さいという場合が＋１とする。

そうでない場合を－１とする。

これを全部の組み合わせについて行う。

この合計を S とすると以下の式で書ける。

\begin{equation} S = \sum_{i \lt j} (\mathrm{sign} (x_j – x_i) \times \mathrm{sign} (y_j – y_i)) \end{equation}

＋１の数と－１の数の差を、全部の組み合わせの数 $ D = \frac{n(n – 1)}{2} $ で割る。

これがケンドールの順位相関係数 $ \tau = \frac{S}{D} $ である。

つまり、順位は使わない順位相関係数ということである。

ケンドールの順位相関係数の計算 同じ値があった場合は？

2つのX,Yペアを取り出したとき、X同士、及び/又は、Y同士が同じ値であった場合はどうするのか？

分母の組み合わせ数から、同じ値のペア数を引くというふうに補正する。

詳しくは下記参考サイトの式を参照。

ケンドールの順位相関係数 | 統計用語集 | 統計WEB

これが、SPSSのクロス集計表の統計で登場するケンドールのタウｂである。

クロス集計表の統計

ケンドールの順位相関係数を計算してみる

R で計算してみる。

Kendall パッケージを使用する。

library(Kendall)
x<-c(1.5,1.5,3,4,6,6,6,8,9.5,9.5,11,12)
y<-c(2.5,2.5,7,4.5,1,4.5,6,11.5,11.5,8.5,8.5,10)

x と y の散布図を書いてみると以下のようになる。

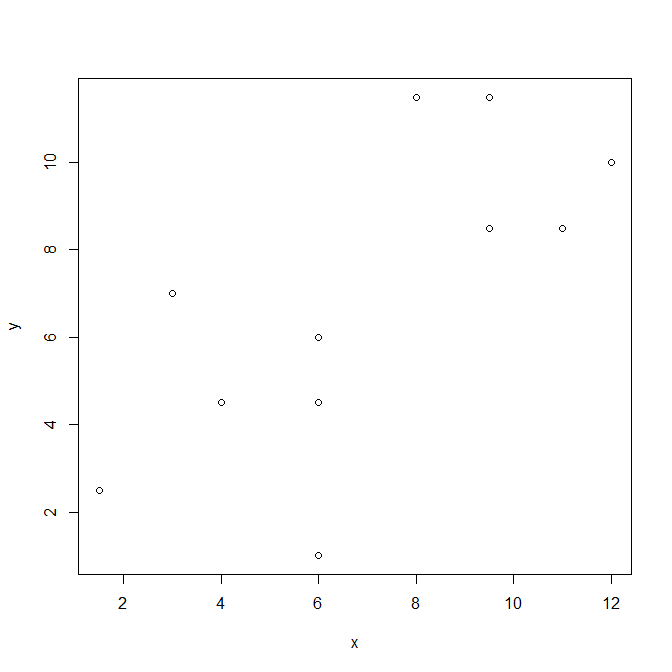
右肩上がりなので、x と y が同じ方向性であるので、プラスの値になることが予想される

ケンドールの順位相関係数を計算すると以下のようになる。

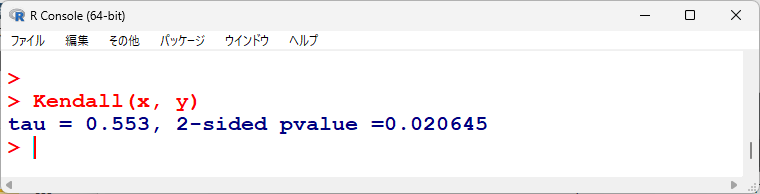
$ \tau = 0.553 $ なので、まずまずの相関と言える。

まとめ

ケンドールの順位相関係数の計算方法を簡単に紹介した。

順位は使わない相関係数である。

参考になれば。

参考サイト

ケンドールの順位相関係数 | 統計用語集 | 統計WEB

↓↓↓図として意味合いが理解したい人はこちら↓↓↓

ケンドールの順位相関係数 統計学入門

↓↓↓SPSSのケンドールのタウｂの説明あり↓↓↓

クロス集計表の統計