カーネル密度推定とはどんな推定で、どんな時に使われるのか?
バンド幅の決め方も紹介
カーネル密度推定とは何か?
とても分かりやすい記事を見つけたので、そのまま引用する。
さて、カーネル密度推定法を大雑把に言うと、
「確率密度が全然わからない確率分布から標本が得られたときに、その標本からできるだけいい感じに元の確率密度を推定する方法」です。
元の確率密度が正規分布だとかポアソン分布だとかだけでもわかっていたら、その期待値や分散などのパラメーターだけ推定すればいい(これをパラメトリックという)のですが、
それさえもわからないときに使われる手法であり、ノンパラメトリックなアプローチと呼ばれます。
通常は、正規分布とか、対数正規分布とか、ポアソン分布とか、母集団の分布の形状がわかっていることが多いが、まったくわからない場合に使うことが想定されている。
分布の形状がわかる場合は、その分布の特徴を示すパラメータを推定することで母集団が推定できる。
まったくわからない場合のカーネル密度推定は、結果はグラフで表現される。
カーネル密度推定法はどんな推定方法なのか?
カーネル密度推定法は、カーネル関数 K を用いて、推定する。
$$ \hat{p} (x) = \frac{1}{nh} \sum_{i=1}^{n} {K \left( \frac{x – X_i}{h} \right)} $$
nはデータの個数、Xi が実際のデータである。
任意に決めたxのときの確率密度をカーネル関数によって推定するという仕組みである。
カーネル密度推定のバンド幅とは?
hはバンド幅と呼ばれて適切に決める必要がある。
h はSilvermannの方法が有名で以下のように計算される。
$$ h = \frac{0.9 \times \min \left( s, \frac{IQR}{1.34} \right)}{n^{1/5}} $$
s はサンプルの標準偏差、IQRは四分位範囲で、標準偏差とIQR/1.34のどちらか小さいほうを0.9倍したものが分子になる。
分母はサンプルサイズの1/5乗。
カーネル関数にはいくつか種類があるが、もっともよく用いられるのは Gaussian ガウス関数である。
これはいわゆる正規分布の関数である。
$$ K(x) = \frac{1}{\sqrt{2 \pi}} \exp{\left( – \frac{x^2}{2} \right)} $$
カーネル密度推定グラフを描いてみる
こちらのサンプルデータを用いてグラフを描いてみる。
統計ソフトRで実行してみる。
クリップボード経由で読み込む。
dat <- read.table("clipboard", header=T)
ヒストグラムを描くとこのようになる。
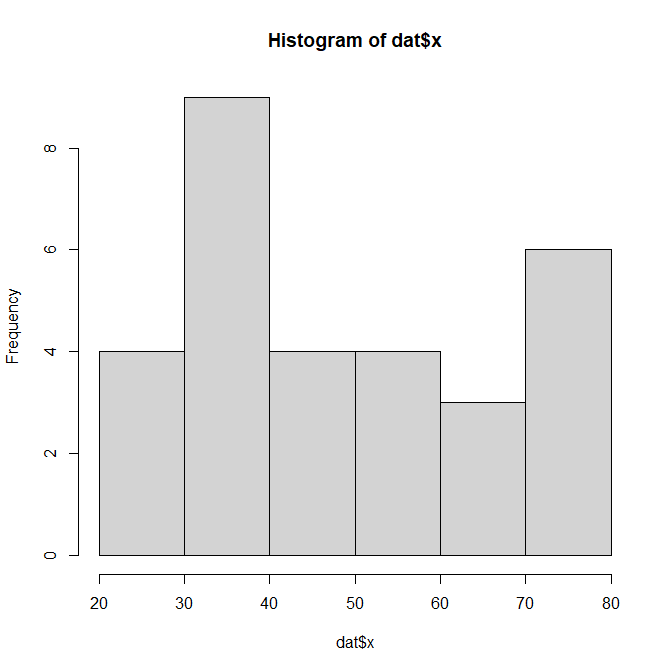
統計ソフトRにはdensity()というカーネル密度推定関数があり、それを使うと簡単に計算できる。
density(dat$x)
バンド幅の設定はどうする?
バンド幅 h は、Silvermannの方法(デフォルト設定)で、カーネル関数はガウス関数(デフォルト設定)を利用する。
計算結果は以下の通り。
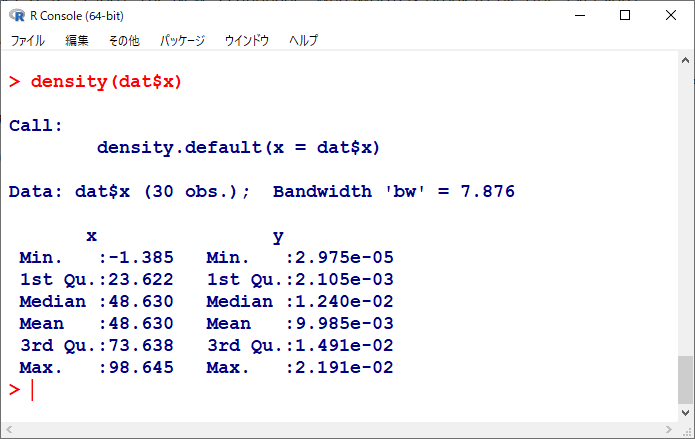
hは Bandwidth ‘bw’で表示されている。
7.876と計算されている。
plot(desity(dat$x))
とplot()関数を実行するとカーネル密度推定グラフが描画される。
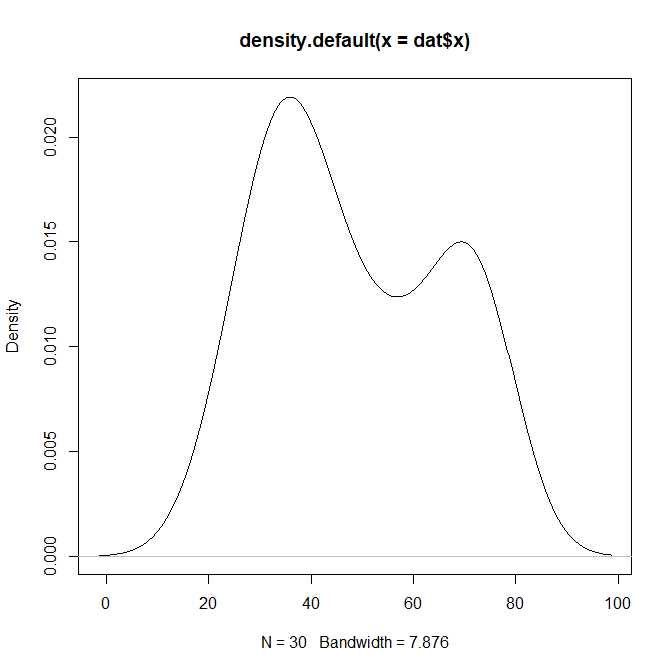
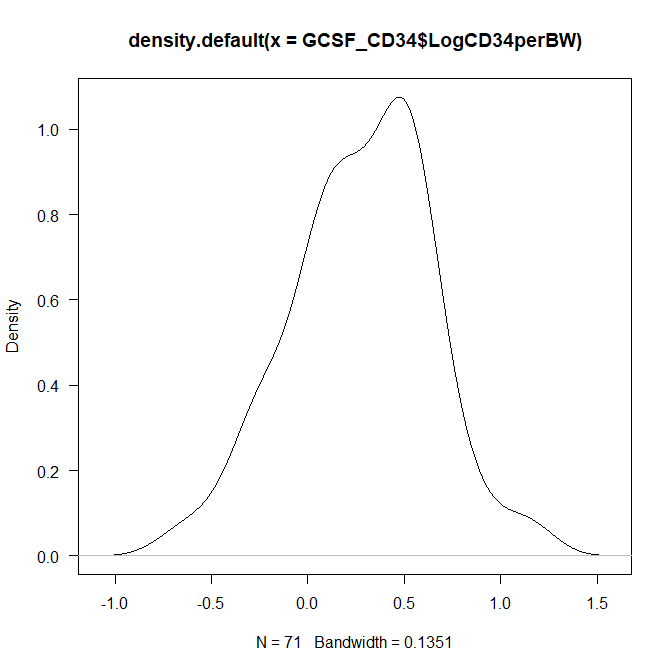
この結果で描かれたグラフが母集団の推定グラフになる。
左右対称の釣り鐘型の正規分布をしていれば、母集団が正規分布であると推定されたことになる。
例えば、もともと以下のような正規分布を思わせるヒストグラムだった場合、
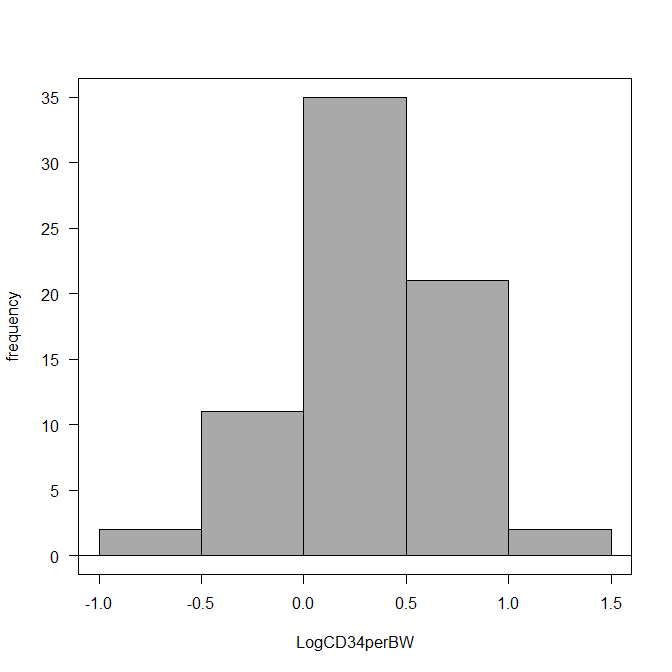
カーネル密度推定グラフを描くと以下のようにほぼ正規分布に近いグラフになる。
まとめ
あるサンプルが得られている時に、ノンパラメトリックに母集団の分布を推定する方法として、カーネル密度推定がある。
カーネル密度推定の方法を簡単に紹介し、統計ソフトRのdensity()関数を使えば、簡単に推定することができ、グラフ描画できることを紹介した。
関連記事

参考資料・サイト
ノンパラメトリック密度推定法
http://ibis.t.u-tokyo.ac.jp/suzuki/lecture/2015/dataanalysis/L9.pdf








コメント