臨床研究や生物学研究において、同じ被験者から複数回測定されたデータ(反復測定データ)は頻繁に登場する。このようなデータは、従来の線形回帰モデルでは適切に解析できない場合がある。なぜなら、同じ被験者からの測定値は互いに相関を持つため、独立性の仮定が満たされないから。線形混合効果モデル(Linear Mixed-Effects Model; LMM)は、このような反復測定データや階層的構造を持つデータの解析に特化した統計モデルであり、個体間のばらつきと個体内での経時的な変化の両方を同時に考慮できる強力なツールである。本記事では、線形混合効果モデルの基本概念から、その仮定、臨床研究での具体例、そして統計ソフトウェアRを用いた計算例までを解説。
線形混合効果モデルの概要
線形混合効果モデル(以下、混合モデルとも呼ぶ)は、固定効果(fixed effects)と変量効果(random effects)という2つの異なる効果を組み合わせた線形モデルである。
- 固定効果(Fixed Effects): 研究者が関心を持つ、母集団全体にわたって固定された効果のこと。例えば、薬剤の効果、治療群と対照群の差、性別の影響などがこれにあたる。従来の線形回帰モデルで扱われる説明変数と同様のものである。
- 変量効果(Random Effects): 個々の被験者やグループ間で異なるばらつきを表現する効果のこと。例えば、被験者ごとのベースライン値の違い、被験者ごとの薬剤への反応性の違いなどがこれにあたる。これらの効果は、特定の被験者やグループに固有のものではなく、より大きな母集団からランダムに抽出されたものと見なされる。変量効果を導入することで、個体内の測定値間の相関をモデルに組み込むことができる。
線形混合効果モデルの基本的な形式は、以下のように表されます。
$$ Y = X \beta + Z \gamma + \varepsilon $$
ここで、
- Y は応答変数(目的変数)のベクトル
- X は固定効果の計画行列
- β は固定効果の係数ベクトル
- Z は変量効果の計画行列
- γ は変量効果の係数ベクトル(確率変数)
- ϵ は残差誤差ベクトル
である。γ と ϵ は、それぞれ特定の分布(通常は正規分布)に従うと仮定する。
混合モデルの計画行列とは
計画行列(Design Matrix)は、統計モデルにおいて説明変数とモデルの係数の関係を表現するために用いられる行列のことである。線形混合効果モデルにおいては、固定効果と変量効果それぞれに対して計画行列が存在する。
- 固定効果の計画行列 (X): 固定効果の計画行列は、従来の線形回帰モデルにおける計画行列と同様の役割を果たす。各行が個々の観測値を表し、各列が固定効果の説明変数(例:介入群か対照群か、性別、時間など)に対応する。例えば、切片、時間、介入群などの固定効果がある場合、これらの変数の値がこの行列に配置される。
- 変量効果の計画行列 (Z): 変量効果の計画行列は、個々の被験者やグループごとに異なる変量効果の構造を定義している。例えば、各被験者に対して異なる切片を持つモデルの場合、Zは各被験者の観測値がどの被験者に属するかを示すような構造になる。また、時間経過に伴う変化が被験者ごとに異なる場合(変量勾配)、Zは時間変数を被験者ごとに紐づけるような構造を持つことになる。Z行列の構造は、モデルでどのような変量効果を考慮するかによって異なる。
これらの計画行列は、モデルの仮定や解析の目的に応じて柔軟に設定される。
混合モデルにおけるモデルの仮定
線形混合効果モデルには、いくつかの重要な仮定がある。これらは、モデルの推定結果の妥当性や信頼性に影響を与えうる。
- 線形性: 応答変数と固定効果および変量効果との関係が線形であること。
- 残差の正規性: 残差誤差 ϵ が平均0の正規分布に従うこと。
- 変量効果の正規性: 変量効果 γ が平均0の正規分布に従うこと。
- 変量効果と残差の独立性: 変量効果と残差誤差が互いに独立であること。
- 均一分散: 残差の分散が均一であること。
- 共分散構造: 変量効果によって捕捉されない残差の共分散構造に関する仮定(例えば、観測値間の独立性や、時間経過に伴う相関の減衰など)。線形混合効果モデルは、変量効果を通じて個体内の測定値間の相関をモデル化するため、残差は条件付きで独立であると仮定されることが多い。
これらの仮定は、診断プロットや統計的検定を用いて確認することが重要である。
臨床研究の具体例
線形混合効果モデルは、様々な臨床研究でその有用性を発揮する。
例:新しい降圧剤の効果を評価する研究
ある新しい降圧剤の効果を評価するために、患者を介入群と対照群に分け、それぞれ6ヶ月間、毎月血圧を測定する研究を計画した。
- 目的: 新しい降圧剤が血圧を低下させる効果があるか、またその効果が時間経過とともにどのように変化するかを評価する。
- 反復測定データ: 各患者は毎月血圧が測定されるため、反復測定データになる。
- 問題点:
- 同じ患者の血圧測定値は、他の患者の測定値と比較したときのような、独立な状態ではない(患者固有のベースライン血圧や薬剤への反応性があるため)。
- 患者によって、ベースラインの血圧が異なる。
- 薬剤の効果が患者によって異なる可能性がある。
線形混合効果モデルの適用:
この研究において、線形混合効果モデルは以下のように適用できる。
- 応答変数: 血圧の値
- 固定効果:
- 時間: 治療開始からの月数(例:0, 1, 2, …, 6)
- 介入群/対照群: 患者がどちらの群に属するかを示すダミー変数
- 時間と群の交互作用: 薬剤の効果が時間経過とともに異なるかどうかを評価するため(例:時間 × 介入群)
- 変量効果:
- 患者ごとの切片: 患者ごとにベースライン血圧が異なることを考慮する(例:各患者に固有のランダム切片)
- (含めることもある) 患者ごとの時間の傾き: 薬剤への反応性が患者によって異なることを考慮する(例:各患者に固有のランダム勾配)
このモデルを使用することで、以下のことを同時に評価できます。
- 薬剤の全体的な効果(固定効果)。
- 時間経過に伴う血圧の変化(固定効果)。
- 患者間のベースライン血圧のばらつき(変量効果)。
- 患者間の薬剤反応性のばらつき(変量効果、もし含める場合)。
- 個々の患者内での血圧の経時的変化のパターン。
従来のANOVAや繰り返し測定ANOVA(反復測定分散分析)では、個体間のばらつきと個体内での経時的な変化をここまで柔軟にモデル化することは困難である。線形混合効果モデルを用いることで、より現実に即したデータ解析が可能となり、介入の真の効果をより正確に推定することができる。
Rによる計算例
ここでは、Rのlme4パッケージとlmerTestパッケージを用いた線形混合効果モデルの簡単な計算例を示す。架空のデータセットを作成し、前述の降圧剤の研究に似た状況の解析結果を示す。
# 必要なパッケージのインストール (初回のみ)
# install.packages("lme4")
# install.packages("lmerTest")
# install.packages("ggplot2") # 結果の可視化用
# パッケージの読み込み
library(lme4)
library(lmerTest) # lmerモデルのP値を得るため
library(ggplot2)
# 架空のデータセットの作成
set.seed(123)
n_patients <- 50 # 患者数
n_visits <- 7 # 測定回数 (ベースライン + 6ヶ月)
# 患者IDとグループの作成
patient_id <- factor(rep(1:n_patients, each = n_visits))
group <- factor(rep(c("Control", "Intervention"), each = n_patients / 2 * n_visits))
# 時間変数の作成 (0から6ヶ月)
time <- rep(0:6, n_patients)
# 患者ごとのベースライン血圧のばらつき (変量切片)
random_intercepts <- rnorm(n_patients, mean = 0, sd = 5)
patient_baseline <- rep(random_intercepts, each = n_visits)
# 固定効果: ベースライン血圧, 時間の効果, 介入群の効果, 時間と介入群の交互作用
# ベースラインの平均血圧を130とする
baseline_bp <- 130
time_effect <- -1.5 # 時間経過で血圧が少し下がる
intervention_effect <- -5 # 介入群は対照群より血圧が低い
interaction_effect <- -1 # 介入群は時間経過とともにさらに血圧が下がる
# 誤差
error <- rnorm(n_patients * n_visits, mean = 0, sd = 3)
# 血圧の計算
blood_pressure <- baseline_bp + patient_baseline +
time * time_effect +
ifelse(group == "Intervention", intervention_effect, 0) +
ifelse(group == "Intervention", time * interaction_effect, 0) +
error
# データフレームの作成
data_bp <- data.frame(
patient_id = patient_id,
group = group,
time = time,
blood_pressure = round(blood_pressure)
)
# データの確認 (一部)
head(data_bp)
summary(data_bp)
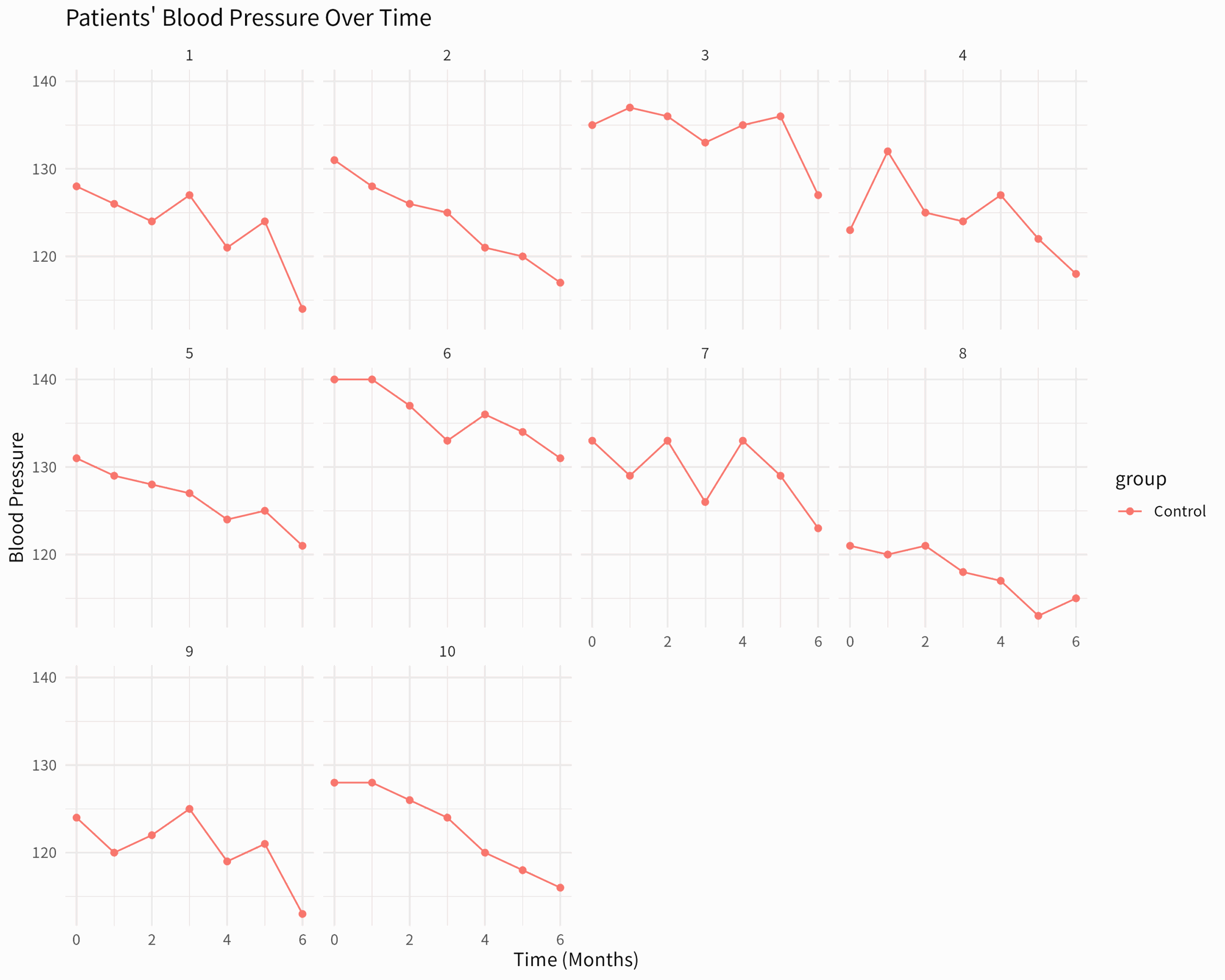
# 時系列データのプロット (一部の患者のみ)
ggplot(subset(data_bp, patient_id %in% c(1:10)), aes(x = time, y = blood_pressure, color = group, group = patient_id)) +
geom_line() +
geom_point() +
facet_wrap(~ patient_id) +
labs(title = "Patients' Blood Pressure Over Time", x = "Time (Months)", y = "Blood Pressure") +
theme_minimal()
# 線形混合効果モデルのフィット
# blood_pressure ~ time * group: 時間、グループ、時間とグループの交互作用を固定効果とする
# (1 | patient_id): 患者ごとの切片を変量効果とする (各患者に固有のベースライン)
model_lmer <- lmer(blood_pressure ~ time * group + (1 | patient_id), data = data_bp)
# モデルの要約
summary(model_lmer)
# 変量勾配も考慮する場合 (各患者で時間経過に伴う血圧変化の傾きが異なる)
# (time | patient_id): 患者ごとの切片と時間に対する傾きの両方を変量効果とする
# model_lmer_rand_slope <- lmer(blood_pressure ~ time * group + (time | patient_id), data = data_bp)
# summary(model_lmer_rand_slope)実行結果:
> # モデルの要約
> summary(model_lmer)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: blood_pressure ~ time * group + (1 | patient_id)
Data: data_bp
REML criterion at convergence: 1907.6
Scaled residuals:
Min 1Q Median 3Q Max
-2.41813 -0.60511 -0.06565 0.60798 3.10148
Random effects:
Groups Name Variance Std.Dev.
patient_id (Intercept) 23.886 4.887
Residual 8.978 2.996
Number of obs: 350, groups: patient_id, 50
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 129.4900 1.0593 59.5124 122.239 < 2e-16 ***
time -1.3786 0.1133 298.0000 -12.173 < 2e-16 ***
groupIntervention -4.3671 1.4981 59.5124 -2.915 0.005 **
time:groupIntervention -0.9557 0.1602 298.0000 -5.967 6.84e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Correlation of Fixed Effects:
(Intr) time grpInt
time -0.321
grpIntrvntn -0.707 0.227
tm:grpIntrv 0.227 -0.707 -0.321
> 出力 summary(model_lmer) の解釈
summary(model_lmer)の出力の Fixed effects に着目する。
- Fixed effects:
Estimate: 各固定効果の推定値。例えば、timeの推定値は、1ヶ月あたりの血圧変化を示している。groupInterventionの推定値は、介入群と対照群の血圧の差を示している。time:groupInterventionの推定値は、介入群における時間経過に伴う血圧変化の勾配が対照群と比べてどれだけ異なるかを示している。Std. Error: 標準誤差。df: 自由度。t value: t値。Pr(>|t|): P値。各固定効果が統計的に有意であるかを示している。
この出力を見ることで、降圧剤が血圧に及ぼす影響(groupIntervention)や、その効果が時間とともにどのように変化するか(time:groupIntervention)を評価することができる。
今回のデータでは、交互作用が有意であるため、時点ごとの比較を EM 平均を用いて検討するのがよい。EM 平均を用いる検討は別記事で紹介する。
まとめ
線形混合効果モデルは、反復測定データや階層的構造を持つデータの解析において、その複雑な構造を適切にモデル化できる非常に強力な統計的アプローチである。固定効果と変量効果を組み合わせることで、研究者が関心のある母集団全体の効果と、個体間のばらつきの両方を同時に考慮し、より精度の高い推定と推論を可能にする。臨床研究をはじめとする様々な分野でその応用が広がっており、適切なモデルの選択と仮定の確認を行うことで、データの持つ情報を最大限に引き出すことができる。





コメント