EZR で線形混合モデルを行う方法と反復測定分散分析との比較

EZR で線形混合モデルの解析方法

反復測定分散分析との違い

線形混合モデルの解析方法の前に 反復測定分散分析

解析の実践はEZRを使って行っていく。

使うデータは、EZR公式マニュアル付属の FCZ_CSA.rda である。

反復測定データ CDratio1, CDratio2, CDratio3を目的変数に、群別変数はFCZを設定する。

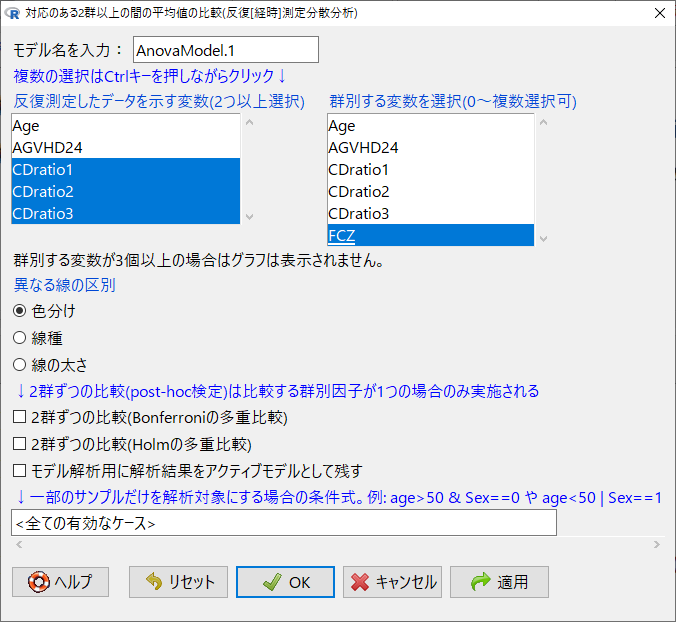
反復測定分散分析を実行すると以下のようになる。

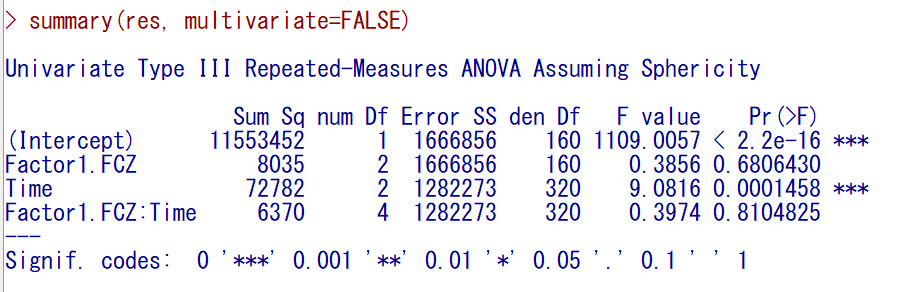
結果出力のメインの部分

３回測定の時間の項 Time が統計学的有意で、群別変数と交互作用（群ごとの時間の影響）は有意でなかった。

線形混合モデルの解析方法 時間の因子をカテゴリカルデータとした場合

公式マニュアルどおりに横持ちのデータを縦持ちのデータに変換する。

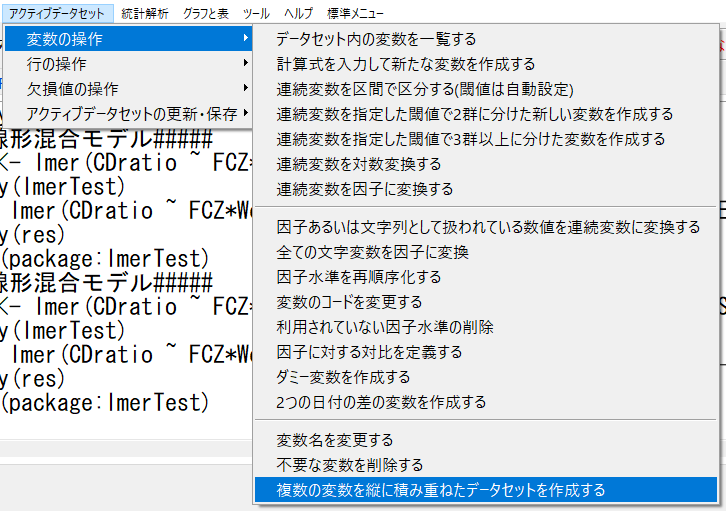
「複数の変数を縦に積み重ねたデータセットを作成する」を用いる

まず、時間の因子をカテゴリカルデータとして投入して解析を実行する。

EZRのメニューから線形混合モデルを選択し、以下のように入力する。

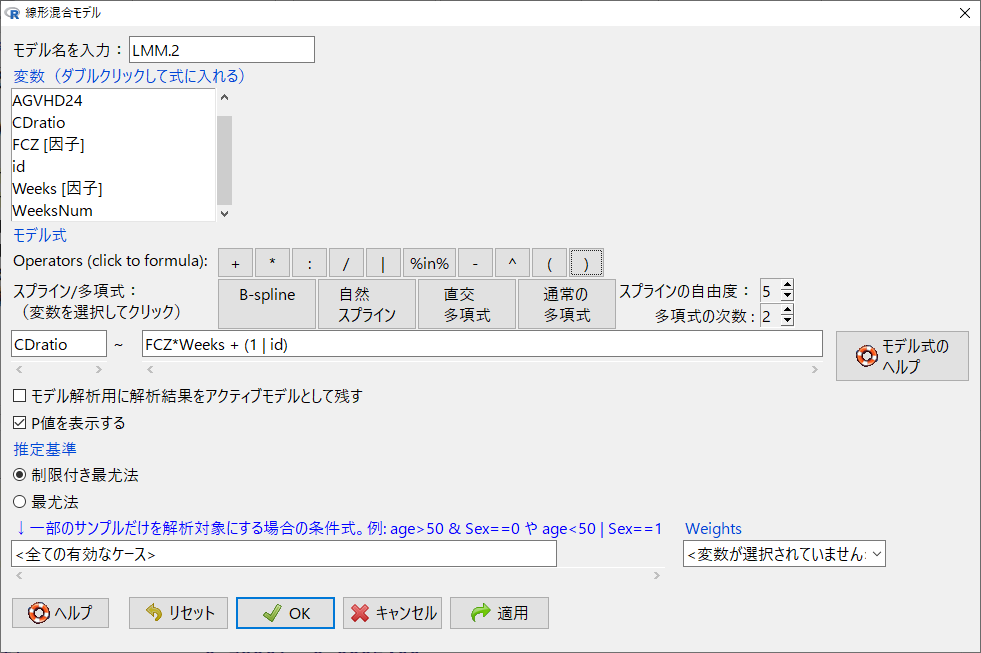
モデル式を入力したところ

モデル式は以下の通りである。

CDratio ~ FCZ * Weeks + (1 | id)

チルダ（~）の左側が目的変数 CDratio 、右側が独立変数で、グループ変数のFCZと時間の変数Weeksを、主効果と交互作用をいっぺんにアスタリスク（*）でつないで投入している。

さらに、プラスでつないで、カッコ内に 1 と id が バーティカルバー (vertical bar) ( | ) をはさんで投入されている。

このカッコ内は、変量効果を指定する変数名を書き入れるところで、バーティカルバーの左は、変量効果と考える傾きとなる連続データの変数を指定する。

1の場合は、傾きの変動効果は考えないモデルとなる。

バーティカルバーの右側は、切片の変動効果で、反復測定データの場合、症例個人を表すIDを入れることが多い。

症例ごとの個人差を、回帰直線の切片が異なると考えることで、考慮する方法である。

この点が、線形混合モデルの利点の一つ。

分散分析はこの個人差を考慮できない。

これでOKをクリックすると以下の結果が出力される。

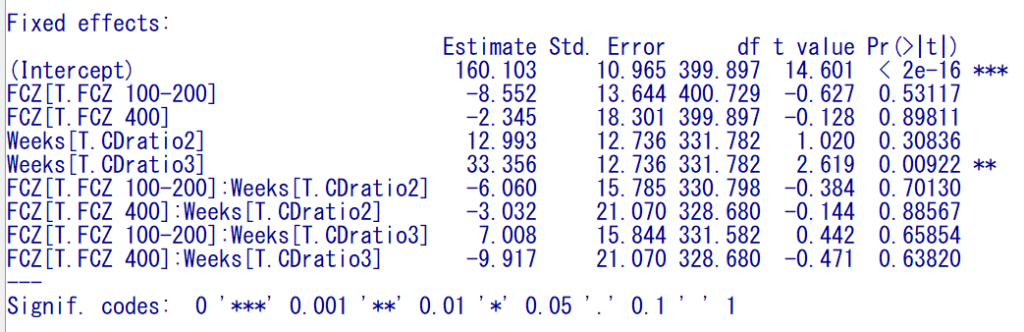
結果の主要な部分

FCZの群間には差がなく、Weeks１と３が有意に異なるという結果だ。

群間と時間の交互作用もない。

線形混合モデルの解析方法 時間の項を連続量で投入した場合

この結果は、時間の項を因子で投入したが、連続量で投入することもできる。

直線的な関係があると考えられれば、連続量で投入してもよい。

カテゴリカルデータで投入した上記の結果から、Week 1 と 2 は、約 13 異なり、Week 2 と 3 は、約 20 異なるので、厳密には直線的とは言い難いが、連続でもやってみると、以下のようになる。

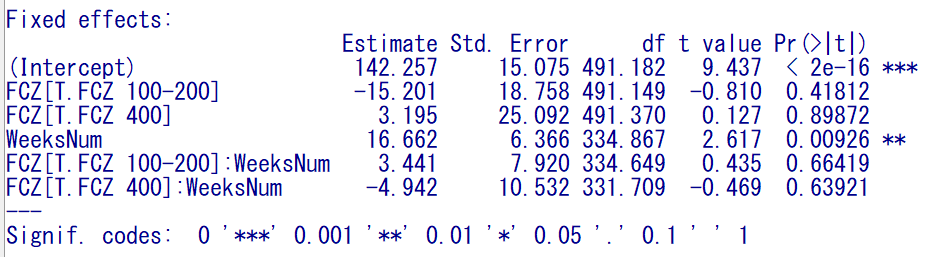
時間の項を連続量にした

WeeksNum の Estimate を見ると、Week 2 の推定値約 13 とWeek 3 の推定値約 33 の平均の約 16.7 となった。

有意確率は因子で投入した場合と変わらなかった。

まとめ

EZRで反復測定データを、線形混合モデルで解析してみた。

反復測定分散分析と比べた利点として、反復データに何回か欠測値があっても、症例ごと削除されることがない点がある。

また、反復測定分散分析では考慮できない個人差を考慮することができる。

偏回帰係数の推定もできる。

参考になれば。

参考書籍