重回帰分析は行列計算をしているわけだが、実際どのような計算をしているのか、R を使って計算してみる。
サンプルデータの準備
使用するデータは ISLR パッケージの Carseats データ。
これはチャイルドシートの売り上げデータ。
パッケージのインストール方法は以下の通り。
install.packages('ISLR')
パッケージインストールの過去記事はこちら。

データセット内の連続データのみを扱う。
library(ISLR)
str(Carseats)
Carseats2 <- Carseats[,c(1:6,8,9)]
str(Carseats)
使用するデータは以下の通り。
Salesをほかの7つの変数で予測する重回帰モデルを作る。
> str(Carseats2)
'data.frame': 400 obs. of 8 variables:
$ Sales : num 9.5 11.22 10.06 7.4 4.15 ...
$ CompPrice : num 138 111 113 117 141 124 115 136 132 132 ...
$ Income : num 73 48 35 100 64 113 105 81 110 113 ...
$ Advertising: num 11 16 10 4 3 13 0 15 0 0 ...
$ Population : num 276 260 269 466 340 501 45 425 108 131 ...
$ Price : num 120 83 80 97 128 72 108 120 124 124 ...
$ Age : num 42 65 59 55 38 78 71 67 76 76 ...
$ Education : num 17 10 12 14 13 16 15 10 10 17 ...
lm() で計算してみる
行列を使って Step by Step で計算してみる前に、lm() を使って計算してみる。
lm2 <- lm(Sales~.,data=Carseats2)
summary(lm2)
結果はこちら。
> summary(lm2)
Call:
lm(formula = Sales ~ ., data = Carseats2)
Residuals:
Min 1Q Median 3Q Max
-5.0598 -1.3515 -0.1739 1.1331 4.8304
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.7076934 1.1176260 6.896 2.15e-11 ***
CompPrice 0.0939149 0.0078395 11.980 < 2e-16 ***
Income 0.0128717 0.0034757 3.703 0.000243 ***
Advertising 0.1308637 0.0151219 8.654 < 2e-16 ***
Population -0.0001239 0.0006877 -0.180 0.857092
Price -0.0925226 0.0050521 -18.314 < 2e-16 ***
Age -0.0449743 0.0060083 -7.485 4.75e-13 ***
Education -0.0399844 0.0371257 -1.077 0.282142
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.929 on 392 degrees of freedom
Multiple R-squared: 0.5417, Adjusted R-squared: 0.5335
F-statistic: 66.18 on 7 and 392 DF, p-value: < 2.2e-16
行列計算で実行する方法
データを行列にする
nとpはサンプルサイズとパラメータの数。
データを行列にする必要がある。
Xの最初の列に切片としてすべてのデータ行に1を入力した。
ちなみに[,1]は一列目のみを取り出す指示、[,-1]は一列目以外を取り出す指示。
as.matrix() は行列として扱う指示。
y <- as.matrix(Carseats2[,1])
n <- length(y)
p <- length(Carseats2[,-1])
X <- as.matrix(cbind("Intercept"=rep(1,n),Carseats2[,-1]))
str(y)
str(X)
yとXはstr()では以下のように見える。
> str(y)
num [1:400, 1] 9.5 11.22 10.06 7.4 4.15 ...
> str(X)
num [1:400, 1:8] 1 1 1 1 1 1 1 1 1 1 ...
- attr(*, "dimnames")=List of 2
..$ : chr [1:400] "1" "2" "3" "4" ...
..$ : chr [1:8] "Intercept" "CompPrice" "Income" "Advertising" ...
回帰係数ベクトルを求める(最小二乗法を行列で)
回帰係数の推定値ベクトル $ \boldsymbol{\hat{\beta}} $ を求めるための式は以下の通り。
$$ \boldsymbol{\hat{\beta}} = (\boldsymbol{X}^t \boldsymbol{X})^{-1} \boldsymbol{X}^t \boldsymbol{y} $$
R で計算してみる。
まず、$ \boldsymbol{X}^t \boldsymbol{X} $
これは転置 t() と、行列の掛け算%*%を使って以下のように書く。
t(X) %*% X
すると、行列にパラメータが配置された8×8の行列が計算される。
> t(X) %*% X
Intercept CompPrice Income Advertising Population Price Age Education
Intercept 400 49990 27463 2654 105936 46318 21329 5560
CompPrice 49990 6341324 3418378 330699 13153953 5873316 2655656 695265
Income 27463 3418378 2198045 186598 7260338 3165088 1463551 380072
Advertising 2654 330699 186598 35256 806772 310118 141322 36657
Population 105936 13153953 7260338 806772 36722296 12249952 5608130 1456118
Price 46318 5873316 3165088 310118 12249952 5587066 2454154 644111
Age 21329 2655656 1463551 141322 5608130 2454154 1242033 296583
Education 5560 695265 380072 36657 1456118 644111 296583 80024
次に、逆行列 $ (\boldsymbol{X}^t \boldsymbol{X})^{-1} $ はどうやって書くか。
これはsolve() を使って文字通り「解く」。
結果は8×8の行列になっている。
solve(t(X)%*%X)
この逆行列に右から $ \boldsymbol{X} $ の転置行列をかけて、さらに $\boldsymbol{y} $ を掛けると回帰係数ベクトルが計算される。
solve(t(X)%*%X) %*% t(X) %*% y
結果はこちら。
これがいわゆる最小二乗法で、行列を使うとこんな計算になる。
> solve(t(X)%*%X) %*% t(X) %*% y
[,1]
Intercept 7.7076934384
CompPrice 0.0939149066
Income 0.0128717129
Advertising 0.1308636707
Population -0.0001239252
Price -0.0925226099
Age -0.0449743402
Education -0.0399844437
これは、lm() を使った時のcoefficientsに一致する。
Estimateの列の数値が一致しているのがわかる。
> summary(lm2)$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.7076934384 1.1176259965 6.8964873 2.145154e-11
CompPrice 0.0939149066 0.0078395225 11.9796718 2.153866e-28
Income 0.0128717129 0.0034756701 3.7033759 2.432641e-04
Advertising 0.1308636707 0.0151219066 8.6539134 1.302560e-16
Population -0.0001239252 0.0006877272 -0.1801952 8.570924e-01
Price -0.0925226099 0.0050520870 -18.3137403 1.409811e-54
Age -0.0449743402 0.0060082977 -7.4853715 4.751078e-13
Education -0.0399844437 0.0371257460 -1.0770004 2.821424e-01
回帰係数ベクトルに beta という名前を付けておく。
beta <- solve(t(X)%*%X) %*% t(X) %*% y
予測値y.hatを求めて、実測値yと散布図を描いてみる
実測値ベクトル $ \boldsymbol{X} $ と回帰係数ベクトル $ \boldsymbol{\hat{\beta}} $ を使って予測値 $ \hat{y} $ を計算する。
行列表現をすれば以下のようになる。
$$ \boldsymbol{\hat{y}} = \boldsymbol{X \beta} $$
R では、以下の通りのスクリプトになる。
予測値をy.hatとした。
y.hat <- X %*% beta
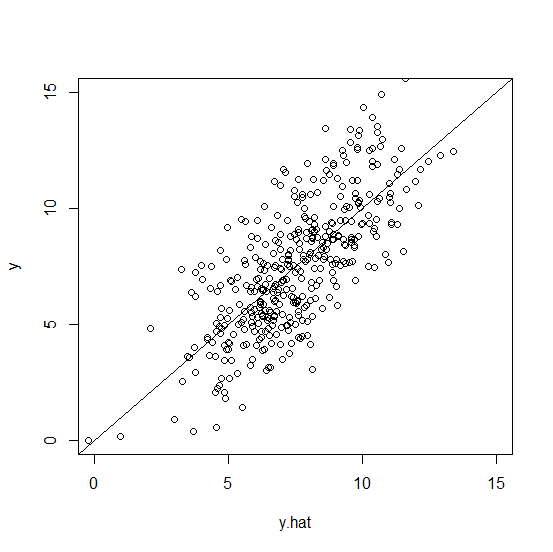
実測値 y と予測値 y.hat の散布図を描いてみた。
切片 0、傾き 1 の直線 y = x も描き入れた。
実測値と予測値が一致すれば直線状に並ぶはずだ。
実際には完全には予測できないので、直線状には並ばない。
plot(y.hat,y, xlim=c(0,15),ylim=c(0,15))
abline(a=0,b=1)
分散共分散行列を求める
次に、回帰係数の検定の準備として、分散共分散行列(V.beta)を求める。
V.betaの計算のために、誤差分散 sigmaE2 を先に計算しておく。
sigmaE2 <- sum((y-y.hat)^2)/(n-p-1)
V.beta <- sigmaE2*solve(t(X)%*%X)
回帰係数の検定
回帰係数の検定は、回帰係数の推定値と回帰係数の標準誤差の比を検定統計量として実施する。
回帰係数の標準誤差は、先ほど計算した分散共分散行列の対角成分 diag() の平方根 sqrt() だ。
SE.beta <- sqrt(diag(V.beta))
t <- beta/SE.beta
pt(abs(t), n-p-1, lower.tail=FALSE)*2
標準誤差(SE.beta)は以下の通り。
> matrix(SE.beta)
[,1]
[1,] 1.1176259965
[2,] 0.0078395225
[3,] 0.0034756701
[4,] 0.0151219066
[5,] 0.0006877272
[6,] 0.0050520870
[7,] 0.0060082977
[8,] 0.0371257460
t値は、回帰係数と標準誤差の比で計算される。
> t
[,1]
Intercept 6.8964873
CompPrice 11.9796718
Income 3.7033759
Advertising 8.6539134
Population -0.1801952
Price -18.3137403
Age -7.4853715
Education -1.0770004
最後に有意確率は以下の通り。
> pt(abs(t), n-p-1, lower.tail=FALSE)*2
[,1]
Intercept 2.145154e-11
CompPrice 2.153866e-28
Income 2.432641e-04
Advertising 1.302560e-16
Population 8.570924e-01
Price 1.409811e-54
Age 4.751078e-13
Education 2.821424e-01
これらはすべてlm() を使った結果と一致する。
> summary(lm2)$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.7076934384 1.1176259965 6.8964873 2.145154e-11
CompPrice 0.0939149066 0.0078395225 11.9796718 2.153866e-28
Income 0.0128717129 0.0034756701 3.7033759 2.432641e-04
Advertising 0.1308636707 0.0151219066 8.6539134 1.302560e-16
Population -0.0001239252 0.0006877272 -0.1801952 8.570924e-01
Price -0.0925226099 0.0050520870 -18.3137403 1.409811e-54
Age -0.0449743402 0.0060082977 -7.4853715 4.751078e-13
Education -0.0399844437 0.0371257460 -1.0770004 2.821424e-01
重相関係数と寄与率
最後に、重相関係数と寄与率(重相関係数の二乗)の計算を示す。
重回帰式の当てはまりの良さを表す指標の一つが寄与率だ。
重相関係数は寄与率の平方根で、実測値 y と予測値 y.hat の相関係数である。
重相関係数は0.735976である。
> cor.test(y,y.hat)
Pearson's product-moment correlation
data: y and y.hat
t = 21.688, df = 398, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.6875397 0.7778921
sample estimates:
cor
0.735976
寄与率は、0.5416606である。
> R2 <- cor(y,y.hat)^2
> R2
[,1]
[1,] 0.5416606
寄与率がゼロでないのを確認する検定は以下の通り。
F <- (R2/p)/((1-R2)/(n-p-1))
pF <- pf(F, p, n-p-1, lower.tail=FALSE)
結果は以下の通り。
> F
[,1]
[1,] 66.18021
> pF
[,1]
[1,] 1.413772e-62
寄与率及び寄与率の検定結果は、lm() の summary()で表示される最下段の記述に現れる。
Multiple R-squared: 0.5417, Adjusted R-squared: 0.5335
F-statistic: 66.18 on 7 and 392 DF, p-value: < 2.2e-16
まとめ
重回帰分析を step by step で R を用いて、行列計算で実行してみた。
参考になれば。
参考書籍
教科書は、「医学への統計学」
15.3 重回帰分析

新版はこちら






コメント
コメント一覧 (1件)
[…] R で行列計算を使って重回帰分析を行う方法 […]