目的変数が正規分布している必要はない。
説明変数も正規分布している必要はない。
前提知識
実際に測定された目的変数を実測値と言う。
回帰式で計算された目的変数を予測値と言う。
実測値と予測値の差を残差と言う。
正式には母集団の誤差項の話になるが、サンプルからはその代用として残差を計算することができ、実際は残差で以下の仮定を確認することになる。
対象にしている回帰モデルは、いわゆる通常の最小2乗法で計算される線形回帰モデルである。
英語では、Ordinary Leaset Squares (OLS) Linear Regressionと言われたりする。
仮定1:回帰モデルは線形である
ここで取り上げる回帰モデルは、係数と誤差項で以下のように記述されるモデルである。
$$ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k + \varepsilon $$
$ \beta $ が係数(偏回帰係数)であり、$ \varepsilon $ が誤差である。
線形でない場合は、非線形モデルとなる。
ここでは非線形モデルは対象外で話を進める。
仮定2:誤差項は母平均ゼロである
誤差項は、独立変数で説明しない従属変数の変動を表している。
ランダムな確率が誤差項の値を決めている。
線形回帰がバイアスなしになるためには、誤差項の平均値がゼロである必要がある。
仮定3:すべての独立変数は誤差項と相関がない
もし、独立変数が誤差項と相関していれば、独立変数を誤差項の予測に使えてしまう。
これは、誤差項が予測不能なランダムエラーを表現しているという考えに反する。
独立変数と誤差項の相関部分を、線形回帰モデルそのものに組み込む方法を見つけ出す必要がある。
仮定4:誤差項の値は互いに相関していない
誤差項のある値が次の誤差項の値を予測してはいけない。
例えば、もし、ある誤差項の値が正で、その後の誤差も正である確率が、どんどんと上昇していく場合は、正の相関である。
もし、次の誤差が反対の符号を持つ確率が高い場合は、負の相関である。
この問題は、serial correlation、自己相関として知られている。
Serial correlationは、時系列モデルで起こりやすい。
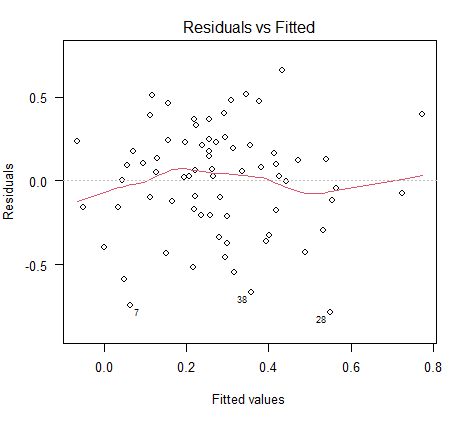
仮定5:誤差項は一定の分散を持つ
これを heteroscedasticity がないとも言う。
分散の異質性(異なること)がないという意味である。
誤差の分散が一定である必要がある。
言い換えれば、誤差の分散が実測値によって変化しないということだ。
この好ましい状態のことを homoscedasticity 均質分散性と言う。
分散が異なることは、heteroscedasticity 異質分散性と言う。
予測値をX軸、残差(誤差の代用)をY軸に置いた散布図を描くと、分散が均質か、異質かがよくわかる。
仮定6:他の説明変数の線形関数関係にある独立変数がない
二つの変数間において、ピアソンの積率相関係数(いわゆる相関係数)が1又はー1であるとき、完璧な相関関係である。
片方の変数が変わると、もう一方も完全に固定した割合で変化する。
2つの変数が一致して動くという意味だ。
この完璧な相関は、2つの変数が同じ変数なのに違う形をしていることを意味している。
例えば、ゲームの勝利と敗北は完璧に負の相関だ。
また、摂氏と華氏の温度は、完璧に正の相関をする。
線形回帰では、完璧に相関している場合、ある変数ともう一つの変数を峻別することができない。
完璧な相関関係の独立変数たちを含むモデルを指定した場合、統計ソフトはデータをモデルにフィットさせられずに、エラーメッセージが出るだろう。
その場合は、それ以上進むためには、モデルから完璧な相関関係の独立変数たちのうち一つを取り除く必要がある。
これは多重共線性のことを言っている。
VIFで、5以上は疑い、10以上は確定として、その変数は取り除くのが望ましい。

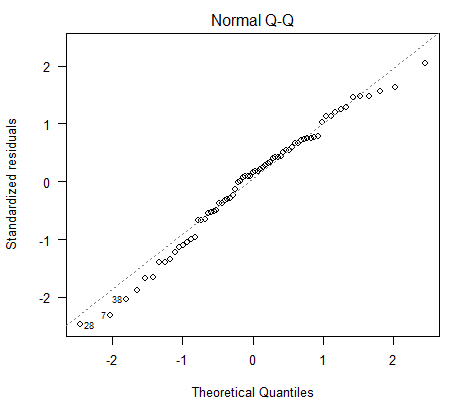
仮定7:誤差項が正規分布している(オプション、非必須)
線形回帰は、最小の分散で、偏りのない推定値を求めるためであれば、誤差項が正規分布していることを必須とはしていない。
しかしながら、誤差項の正規性という仮定を満たすと、統計的仮説検定が実施できて、信頼性の高い信頼区間や予測区間が計算できる。
残差(誤差項の代用)が正規分布に従っているかどうかを確認する簡単な方法は、正規確率プロットで評価する方法だ。
残差が、正規確率プロットの直線状に乗っている場合、正規分布している。
まとめ
いわゆる通常の最小2乗法で偏回帰係数を求める線形回帰では、上記の7つの仮定がおかれている。
この中に、独立変数(説明変数)の正規性もなければ、従属変数(目的変数)の正規性もない。
必須ではないが、残差(誤差項)が正規分布していればなおよしという程度である。
回帰分析のために、説明変数が正規分布している必要はなく、目的変数が正規分布している必要もない。
参照元サイト
7 Classical Assumptions of Ordinary Least Squares (OLS) Linear Regression – Statistics By Jim






コメント
コメント一覧 (3件)
[…] 回帰分析における 7 つの仮定 目的変数が正規分布している必要はない。 […]
[…] 回帰分析における 7 つの仮定 目的変数が正規分布している必要はない。 […]
[…] 回帰分析における 7 つの仮定 目的変数が正規分布している必要はない。 […]