生存時間解析に登場する群間比較検定のログランク検定。
いったいどんな計算をしているのか?
わかりやすく解説。
ログランク検定とは?
ログランク検定とは、以下のようなカプランマイヤー曲線で描かれるような生存時間データを群間比較する検定である。
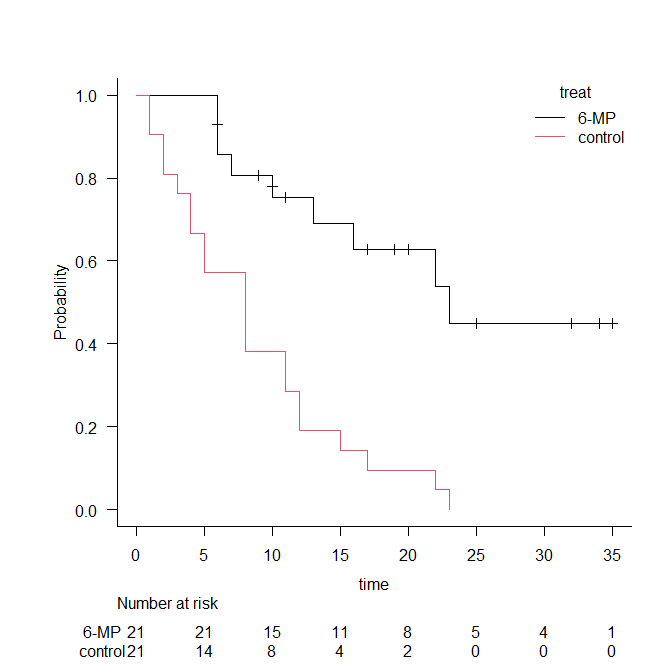
実際どのような計算をしているのだろうか?
ログランク検定はどのような計算をしているのか?
ログランク検定の帰無仮説は母集団におけるイベントの観測値と期待値に差がないというものである。
検定統計量は、イベントが起きた時点ごとの観測値と期待値の差分の合計を、時点ごとの分散の合計の平方根、つまり標準偏差的な数値で割ったものになる。
添え字等を省くと以下のような式になる。
$$ Z = \frac{\sum (O – E)}{\sqrt{\sum V}} $$
詳しくはWikipedia参照。
EZRでは、ログランク検定の検定統計量として、カイ2乗値と表示され、上記の検定統計量 Z の2乗が出力される。
検定統計量 Z は、いわゆるカイ2乗検定の検定統計量にとても似ている。
カイ 2 乗検定の検定統計量は、添え字等を省いて書いてみると、以下のような式になる。
$$ \chi^2 = \sum{\frac{(O – E)^2}{E}} $$
カイ2乗検定の詳細はWikipedia参照。
ログランク検定は生存時間自体を使っていない!?
上記のログランク検定の検定統計量の主体はイベントの観測値、つまり発生したイベント数である。
検定統計量の式で省略した添え字は、イベントが観測された時点の順番と、グループの番号である。
つまり、検定統計量に「時間」そのものは入っていない。
生存時間解析ではあるが、生存時間そのものは、解析してはいない。
ログランク検定はどのような計算をしているのか?
では、ログランク検定はどのような計算をしているのだろうか?
サンプルデータを用いて確認しよう
サンプルデータを用いて計算を再現してみようと思う。
サンプルデータは MASS パッケージの gehan データセットだ。
白血病の患者さんを6-メルカプトプリン(6-MP)で治療した群とコントロール群とで比較した試験のデータである。
上記のカプランマイヤー曲線は、このデータをプロットしたものである。
ログランク検定をしてみると以下のような結果が出力される。
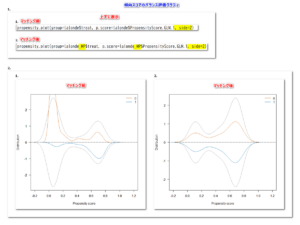
EZRで、「統計解析」→「生存期間の解析」→「Logrank検定」を選択して以下のように指定する。
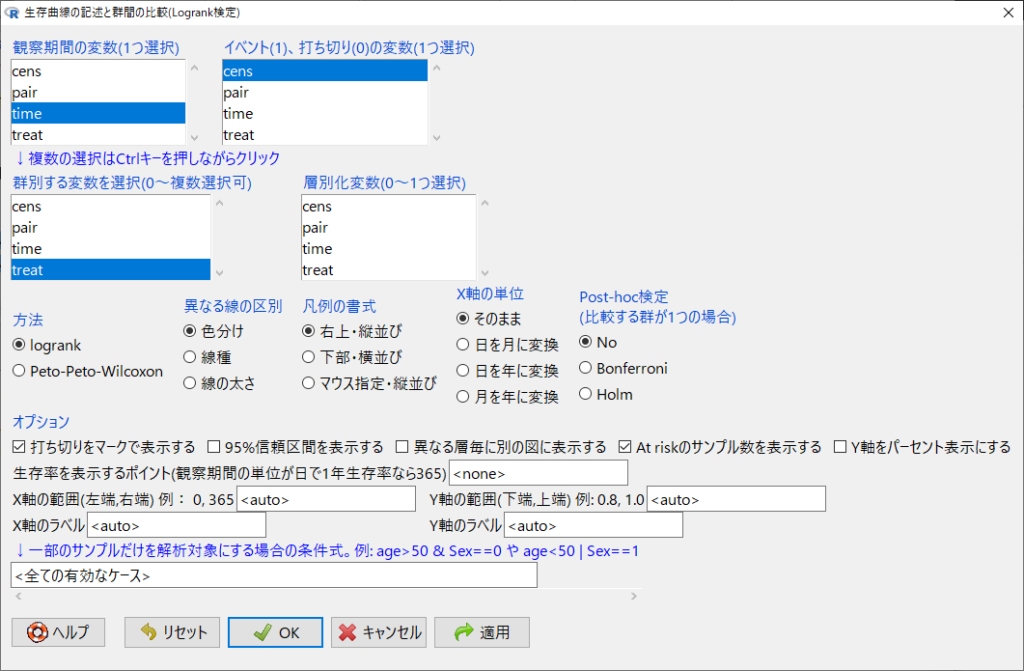
ログランク検定の結果は以下のとおりである。

> (res <- survdiff(Surv(time,cens==1)~treat, data=gehan, rho=0, na.action =
+ na.omit))
Call:
survdiff(formula = Surv(time, cens == 1) ~ treat, data = gehan,
na.action = na.omit, rho = 0)
N Observed Expected (O-E)^2/E (O-E)^2/V
treat=6-MP 21 9 19.3 5.46 16.8
treat=control 21 21 10.7 9.77 16.8
Chisq= 16.8 on 1 degrees of freedom, p= 0.00004
データの加工
gehanはこのようなデータである。
pairになっているが、今回はpairの要素は考慮しない。
timeがイベントもしくは打ち切りまでの観察時間(週)である。
censが1の時はイベント(死亡)発生、0は打ち切り(生存のまま観察終了)である。
treatが6-MP治療群かコントロール群かである。

先ほどカプランマイヤー曲線を描かせて、ログランク検定を行った結果を利用して、時点ごとのイベント数、打ち切り数をまとめたデータセット gehan.O12 を作成する。
gehan.O12 <- with(km, data.frame(treat=c(rep("6-MP",16),rep("CTRL",12)),time,n.risk,n.event,n.censor))
出来上がりがこちら。
timeがイベントもしくは打ち切り発生までの時間、n.riskがtime時点に試験に残っている各群の患者数、n.eventがtime時点でイベントが発生した人数、n.censorが打ち切りとなった人数である。
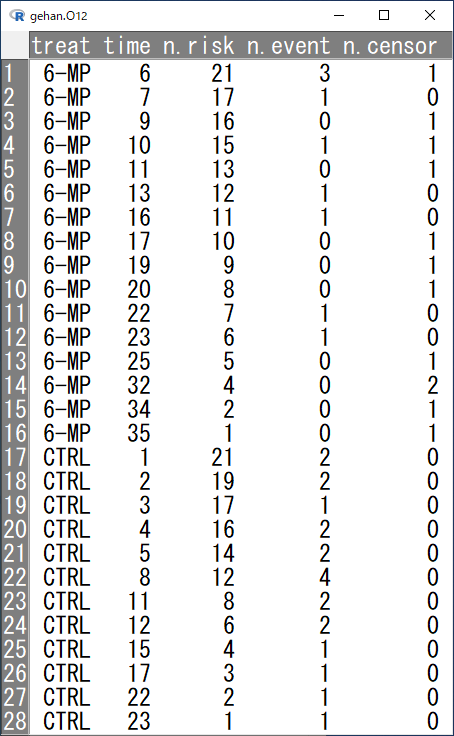
この6-MP群とコントロール群群が縦に積み重なっているものを横に並べたいのだが、EZRでは実施方法がわからず、いったんCSV形式で出力し、エクセルで以下のように加工して、EZRに再度取り込んだ。
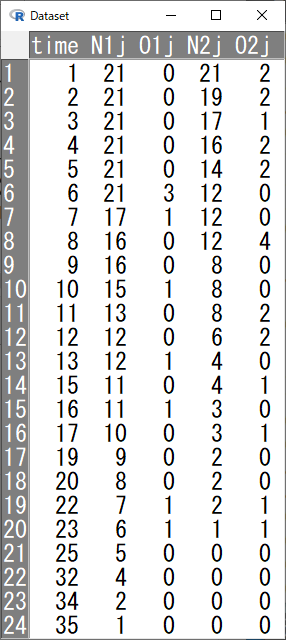
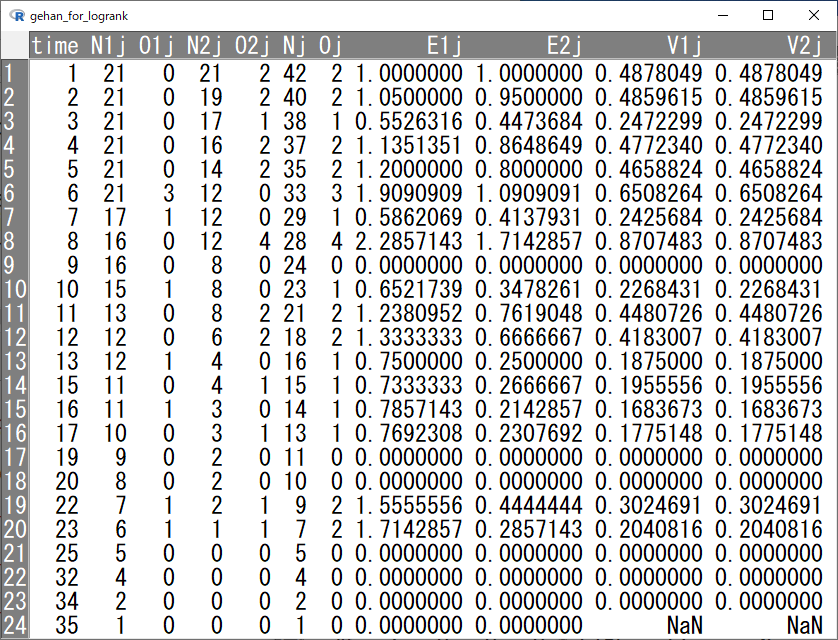
ここで、それぞれの変数の説明をすると、
- time:両群通してイベントか打ち切りが発生した時点までの時間
- N1j:time時点に試験に残っている6-MP群の患者数
- O1j:time時点でイベントが発生した人数
- N2j:time時点のコントロール群の患者数
- O2j:time時点の打ち切り例の人数
である。
このデータをもとに以下のような加工をすると、期待値Eと分散Vが計算できる。添え字は各群(1が6-MP群、2がコントロール群)を示している。
#####計算式を入力して新たな変数を作成する#####
gehan_for_logrank$Nj <- with(gehan_for_logrank, N1j+N2j)
#新しい変数 Nj を作成しました。
#####計算式を入力して新たな変数を作成する#####
gehan_for_logrank$Oj <- with(gehan_for_logrank, O1j+O2j)
#新しい変数 Oj を作成しました。
#####計算式を入力して新たな変数を作成する#####
gehan_for_logrank$E1j <- with(gehan_for_logrank, N1j*Oj/Nj)
#新しい変数 E1j を作成しました。
#####計算式を入力して新たな変数を作成する#####
gehan_for_logrank$E2j <- with(gehan_for_logrank, N2j*Oj/Nj)
#新しい変数 E2j を作成しました。
#####計算式を入力して新たな変数を作成する#####
gehan_for_logrank$V1j <- with(gehan_for_logrank,
E1j*(Nj-Oj)/Nj*(Nj-N1j)/(Nj-1))
#新しい変数 V1j を作成しました。
#####計算式を入力して新たな変数を作成する#####
gehan_for_logrank$V2j <- with(gehan_for_logrank,
E2j*(Nj-Oj)/Nj*(Nj-N2j)/(Nj-1))
#新しい変数 V2j を作成しました。
詳しい計算方法は、Wikipedia参照。
検定統計量Zの計算とp値
ここまで準備が出来たら検定統計量Zを計算する。
> Z <- with(gehan_for_logrank, sum(O1j-E1j)/sqrt(sum(V1j, na.rm=T)))
> Z
[1] -4.097919
このZ値を用いて、標準正規分布を使ってp値を計算する。
pnorm()で、下側の確率が計算できるので、2倍して両側検定とする。
結果としてp値は0.00004となった。
> 2*pnorm(Z)
[1] 0.00004168809
これは先ほどのEZRのメニューからログランク検定を行ったときのp値と同じである。

ちなみにZを2乗すると、カイ2乗値 Chisq=16.8 と一致する。
> Z^2
[1] 16.79294
解説動画
解説動画を作成した。
よければ。
まとめ
生存時間解析で、群間を比較する方法として有名なログランク検定は、どのような検定で、どのような計算をしているかを解説した。
イベントまたは打ち切りの人数と発生した時点の情報は使用するものの、発生までの時間(生存時間)そのものを使ってはいない。
参考になれば。
参考サイト
おすすめ書籍
EZR公式マニュアル








コメント