「なんだか複雑そうな数式や理論が出てきそう…」そう思われた方もいるかもしれない。しかし、ご安心いただきたい。この記事では、マルコフ連鎖モンテカルロ法 (MCMC) という強力な統計的手法について、その基本から応用までを、できる限りわかりやすく解説する。
MCMCは、現代のデータサイエンスにおいて欠かせないツールであり、特にベイズ統計や複雑なモデルの分析でその真価を発揮する。難解に思えるこのMCMCが、どのような原理で動き、どのような問題を解決してくれるのか。この記事を読み終える頃には、きっとその魅力に気づき、データ分析の新たな扉が開かれることであろう。さあ、一緒にMCMCの世界へ踏み出そう。
MCMCの概要
マルコフ連鎖モンテカルロ法 (MCMC) は、ベイズ統計や複雑な確率分布からのサンプリングに不可欠な強力な計算手法である。特に、解析的に扱うことが難しい高次元の分布や、定数部分が不明な分布からのサンプリングにその真価を発揮する。MCMCは、マルコフ連鎖の概念とモンテカルロ法のアイデアを組み合わせることで、対象の分布に従うサンプルを生成し、その分布の特性を近似的に把握することを可能にする。
マルコフ連鎖とは
マルコフ連鎖は、将来の状態が現在の状態のみに依存し、それ以前の状態には依存しないという特性を持つ確率過程である。これを「マルコフ性」と呼ぶ。
- 確率過程: 時間の経過とともに変化する確率変数のシーケンスを指す。
- 遷移核: ある状態から別の状態へ遷移する確率を表す。例えば、現在の状態が x であったときに、次の状態が y になる確率を P(y∣x) のように表す。
- 定常分布: マルコフ連鎖が十分に長い時間進行した後に到達する、変化しない確率分布のことである。定常分布に到達すると、各状態にいる確率が時間とともに変化しなくなる。MCMCでは、この定常分布が私たちがサンプリングしたいターゲットの分布となるようにマルコフ連鎖を設計する。
モンテカルロ法とは
モンテカルロ法は、乱数を用いて数値的な問題を解決する手法の総称である。特に、確率的な現象をシミュレーションしたり、複雑な積分を近似的に計算したりする際に用いられる。例えば、円周率を求めるためにランダムな点を正方形内にプロットし、円の内側に入った点の割合から円周率を推定するといった方法もモンテカルロ法の一つである。統計学においては、ある分布からのサンプルを大量に生成し、それらのサンプルを用いて期待値や分散などを推定する際によく利用される。
マルコフ連鎖とモンテカルロ法を結びつける意義
MCMCの核心は、対象としたい確率分布を定常分布として持つマルコフ連鎖を構築することにある。一度このようなマルコフ連鎖が構築されれば、その連鎖をシミュレートし続けることで、最終的に定常分布(すなわち、ターゲットの分布)に従うサンプルを生成できる。
なぜこれが重要なのか。多くの統計モデル、特にベイズ統計モデルでは、パラメータの事後分布が非常に複雑で、直接サンプリングしたり、解析的に計算したりすることが困難な場合がある。MCMCは、このような直接的な計算が難しい分布からでも、その分布に従うサンプルを「間接的に」生成する道を開く。これにより、サンプリングされたデータを使って、対象となる分布の形状を推定したり、様々な統計量を計算したりすることが可能になる。
事前分布と事後分布
ここで、ベイズ統計における重要な概念である「事前分布」と「事後分布」について解説する。
- 事前分布 (Prior Distribution): データを得る前に、私たちが知りたいパラメータ $ \theta $ がどのような値を取るかについての信念や知識を表す確率分布である。これは、過去の研究結果、専門家の意見、あるいは単なる無情報な仮定(例えば、すべての値が等しい確率で起こりうると仮定する一様分布など)に基づいて設定される。事前分布は、$ P(\theta) $ と表記される。
- 事後分布 (Posterior Distribution): 新しいデータ D を観測した後に、パラメータ $ \theta $ がどのような値を取るかについての更新された信念を表す確率分布である。これは、事前分布とデータから得られた情報(尤度)を組み合わせることで得られる。事後分布は、ベイズの定理によって以下のように計算される。
$$ P(\theta | D) = \frac{P(D|\theta)P(\theta)}{P(D)} $$
ここで、$ P(D∣\theta) $ は尤度 (Likelihood) と呼ばれ、特定のパラメータ $ \theta $ のもとで、観測されたデータ D が得られる確率を示す。P(D) はデータの周辺確率で、正規化定数として機能し、すべての $\theta $ について $ P(D∣\theta)P(\theta) $ を積分(または合計)することで得られる。
事後分布 $ P(\theta∣D) $ は、データ D を考慮に入れた上での、パラメータ $ \theta $ に関する最も包括的な情報を提供する。しかし、特に高次元のパラメータ空間や複雑な尤度関数、事前分布の場合、P(D) の計算(つまり、分母の積分)が非常に困難になることがよくある。MCMCは、この困難な積分を直接計算することなく、事後分布 $ P(\theta∣D) $ から直接サンプルを生成することを可能にする。これが、MCMCがベイズ統計において不可欠なツールとなっている理由である。
MCMCの使い所
MCMCは、以下のような場面で非常に有効である。
- ベイズ統計推論: 事後分布からのサンプリングに必須である。特に、複雑な階層モデルやグラフィカルモデルにおいて威力を発揮する。
- 高次元の積分: 高次元の複雑な関数を積分する際に、モンテカルロ積分の効率を向上させる。
- 物理学や化学におけるシミュレーション: 統計力学における相転移のシミュレーションなど、多様な系で利用される。
- 機械学習: 確率的グラフィカルモデルの学習や推論に用いられることがある。
具体例と R の計算例・可視化
ここでは、最も基本的なMCMCアルゴリズムの一つであるメトロポリス・ヘイスティングス法を用いて、正規分布からのサンプリングを試みてみよう。
ターゲットとする分布を平均0、標準偏差1の標準正規分布 N(0,1) とする。
R 計算例
# ターゲットとなる分布 (標準正規分布の確率密度関数)
target_density <- function(x) {
dnorm(x, mean = 0, sd = 1)
}
# メトロポリス・ヘイスティングス法の実装
mcmc_mh <- function(n_iter, initial_x, proposal_sd) {
# サンプルを保存するベクトル
samples <- rep(NA, n_iter)
current_x <- initial_x
for (i in 1:n_iter) {
# 提案分布から新しい候補を生成 (ここでは正規分布を使用)
proposed_x <- rnorm(1, mean = current_x, sd = proposal_sd)
# 受容確率の計算
# α = min(1, (ターゲット密度(提案) / ターゲット密度(現在)) * (提案分布(現在|提案) / 提案分布(提案|現在)))
# 提案分布が対称 (N(current, sigma) -> N(proposed, sigma)) なので、後半は1になる
acceptance_ratio <- target_density(proposed_x) / target_density(current_x)
alpha <- min(1, acceptance_ratio)
# 乱数を生成し、受容するかどうかを決定
if (runif(1) < alpha) {
current_x <- proposed_x # 受容
}
samples[i] <- current_x # 現在の状態をサンプルとして記録
}
return(samples)
}
# MCMCの実行
set.seed(123) # 再現性のためにシードを設定
n_iterations <- 5000 # 繰り返し回数
initial_value <- 0 # 初期値
proposal_sd_value <- 1 # 提案分布の標準偏差
mcmc_samples <- mcmc_mh(n_iterations, initial_value, proposal_sd_value)
# 結果の可視化
hist(mcmc_samples[1001:n_iterations], # バーンイン期間を除外
freq = FALSE,
main = "MCMCサンプルによる標準正規分布の近似",
xlab = "値",
ylab = "密度",
col = "lightblue",
border = "white"
)
# 真の標準正規分布の密度曲線を重ねて描画
curve(dnorm(x, mean = 0, sd = 1), add = TRUE, col = "red", lwd = 2)
# サンプルの推移(トレースプロット)
plot(mcmc_samples, type = "l", main = "MCMCサンプルの推移 (トレースプロット)", xlab = "イテレーション", ylab = "値")
abline(h = mean(mcmc_samples[1001:n_iterations]), col = "blue", lty = 2) # サンプルの平均値
abline(h = 0, col = "green", lty = 2) # 真の平均値
可視化の解釈
上のRコードを実行すると、以下の2つのグラフが得られる。
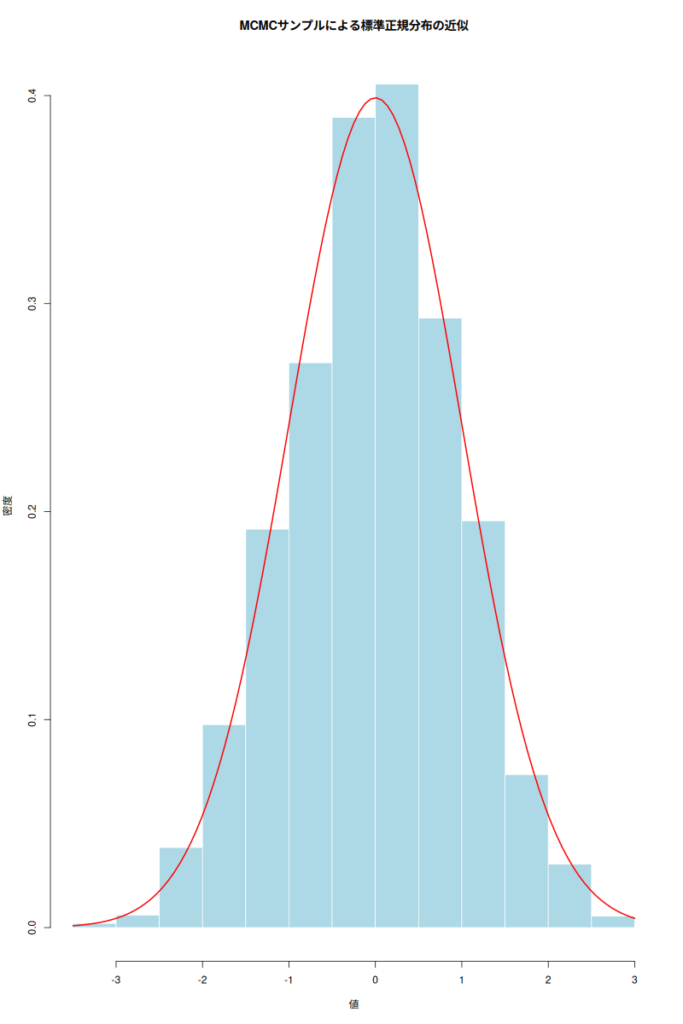
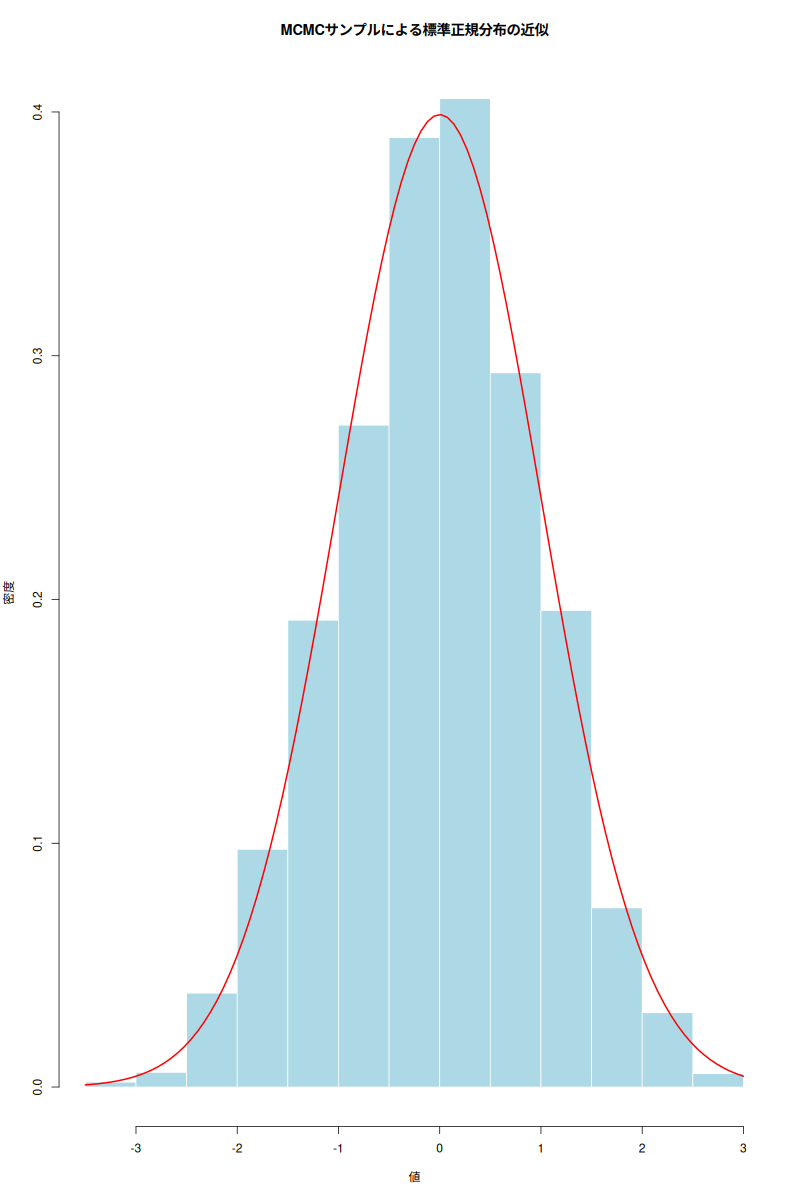
- MCMCサンプルによる標準正規分布の近似: ヒストグラムが標準正規分布の密度曲線(赤線)に近似していることがわかる。これは、MCMCが目的の分布からサンプルを効率的に生成できていることを示している。
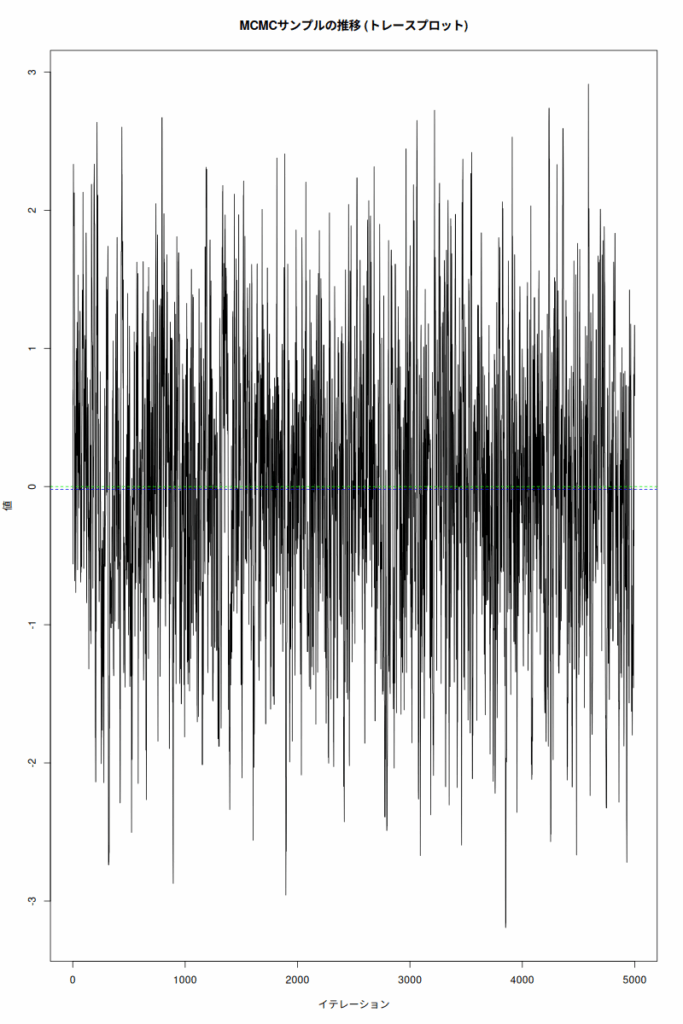
- MCMCサンプルの推移 (トレースプロット): サンプルがどのように推移していったかを示している。連鎖が十分に混合し、特定の値に固まらずに分布全体を探索できているかを確認できる。
結果解釈
MCMCによるサンプリングが成功していれば、生成されたサンプルはターゲットの分布に従うと見なせる。これらのサンプルを用いて、以下のような分析が可能である。
- 期待値の推定: サンプルの平均を計算することで、ターゲット分布の期待値を推定できる。
- 信頼区間(信用区間)の計算: サンプルのパーセンタイルを計算することで、信頼区間(ベイズ統計では信用区間)を推定できる。
- 分布の形状の理解: ヒストグラムや密度プロットを作成することで、ターゲット分布の形状、非対称性、モードなどを視覚的に理解できる。
上記の例では、標準正規分布からのサンプリングを行ったが、実際にはより複雑な多峰性分布や非対称な分布からのサンプリングにMCMCは用いられる。
まとめ
マルコフ連鎖モンテカルロ法 (MCMC) は、複雑な確率分布からのサンプリングを可能にする強力なツールである。マルコフ連鎖の定常分布と、乱数を用いたモンテカルロ法のアイデアを組み合わせることで、直接計算が難しい問題に対しても、統計的な推論を行う道を開く。
ベイズ統計推論の発展に大きく貢献し、現在では統計学、機械学習、物理学など、幅広い分野で不可欠な手法となっている。MCMCを理解し活用することで、より高度なデータ分析やモデリングが可能になるだろう。




コメント