R で反復測定データの平均値の折れ線グラフを書く方法

反復測定データの群ごと時点ごとの平均値を結んだ折れ線グラフを書く方法

反復測定データと平均値の折れ線グラフ

反復測定データとは、同じ対象者がある決まった時点で何回か測定したアウトカムデータのことである

例えば、今回のサンプルデータのように、8, 10, 12, 14 歳の時の測定値といったような、ある一定期間に繰り返し測定したデータを指す

このようなデータを取得したあとは、測定時点ごと、興味がある比較群ごとに平均値を計算して、図示するのがおすすめである

取得したデータの傾向が見て取れるので、統計解析結果を読み取るときに役に立つ

サンプルデータとグループ別集計

サンプルデータは、R の nlme パッケージに含まれる Orthodont というデータセットである

このデータは、男児 16 例と女児 13 例の 8, 10, 12, 14 歳時の下垂体から翼上顎裂と呼ばれる部分までの距離を頭蓋骨の X 線撮影像で測定した値である

データは以下のように縦方向に繰り返し測定値が並んでいるデータセットである

> head(Orthodont)
distance age Subject  Sex
1     26.0   8     M01 Male
2     25.0  10     M01 Male
3     29.0  12     M01 Male
4     31.0  14     M01 Male
5     21.5   8     M02 Male
6     22.5  10     M02 Male

まずは、dplyr パッケージの group_by 関数を使って、性別・年齢別の Distance の平均値、標準偏差、n を集計する

data('Orthodont', package = 'nlme')
library(dplyr)
df <- Orthodont %>%
group_by(Sex, age) %>%
summarise(mean=mean(distance), sd=sd(distance), n=n())
df

集計した結果は、以下のとおり

> df
# A tibble: 8 × 5
# Groups:   Sex [2]
Sex      age  mean    sd     n
<fct>  <dbl> <dbl> <dbl> <int>
1 Male       8  22.9  2.45    16
2 Male      10  23.8  2.14    16
3 Male      12  25.7  2.65    16
4 Male      14  27.5  2.09    16
5 Female     8  21.2  2.12    11
6 Female    10  22.2  1.90    11
7 Female    12  23.1  2.36    11
8 Female    14  24.1  2.44    11

平均値の折れ線グラフ

集計結果を使って、平均値の折れ線グラフを書いていく

ggplot2 パッケージの ggplot() を使って書く

library(ggplot2)
ggplot(data=df, aes(x=age, y=mean, group=Sex, linetype=Sex))+
geom_line(position=position_dodge(0.3))+
geom_point(size=3, position=position_dodge(0.3))+
geom_errorbar(aes(ymax=mean+sd, ymin=mean-sd), width=0.3,
position=position_dodge(0.3))+
labs(x='Age (years)', y='Distance')+
theme_classic()

data= にデータフレームを指定し、aes で X 軸と Y 軸を指定する

linetype= で性別ごとに線種を分ける

geom_line() で折れ線を書き、geom_point() で平均値を点で描画する

geom_errorbar() がエラーバーで、平均に＋もしくはー の標準偏差としている

いずれにも position=position_dodge(0.3) がオプションとして書かれている

これは、性別ごとに書いた線や点を少しだけずらす（その幅は 0.3 で指定）指示である

labs() が軸のラベル指定で、最後に theme_classic() が古典的なスタイルを指定していて、論文等学術的な目的には適切な見た目になる

図にしてみると、以下のとおり

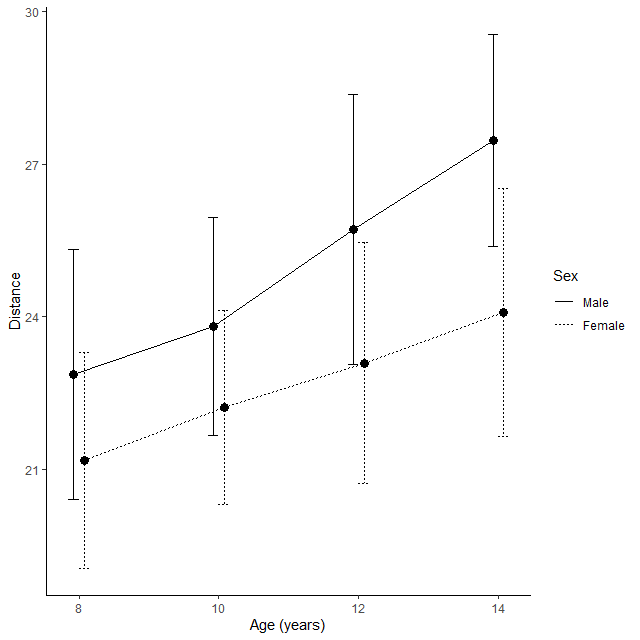
こんなふうにすると様子が一目でわかる

年齢が上がるにつれて、男女とも Distance は大きくなり、女児に比べ男児のほうが大きいことがわかる

これがわかった上で、線形混合モデルなどの解析を行っていくと、結果を正しく解釈できる

まとめ

R で ggplot を使って、反復測定データの平均値の折れ線グラフを書いてみた

参考になれば

関連記事