がん患者さんの生存期間中央値を5年生存率から逆算で求めるにはどうしたらよいか?
R で計算する方法。
5 年生存率から逆算で生存期間中央値を求める計算式
生存確率は、一般論として指数関数で近似できる。
実際には、がんの治療後すぐになくなったり、数年たってから急にお亡くなりになる方が増えたりして、一定ではないことが多いので、パラメータを使わないカプランマイヤー曲線が使われる。
カプランマイヤー曲線とは?
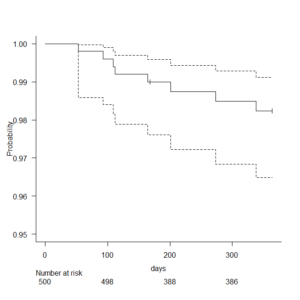
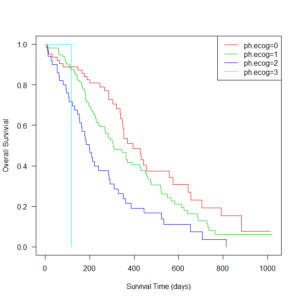
しかしながら、逆算で求めるためには、パラメータを使う計算方法を使う必要がある。
なので、近似的な方法の指数関数を使った方法で計算する。
5年生存率(Five year survival rate, Rとする)は、以下の式で求められる。
$$ R = (1 – r)^5 $$
ここで、r は、年間死亡率(Annual death rate)であり、一定であることが条件。
r を求めるように式を変形すると以下の通りになる。
$$ r = 1 – R^{1/5} $$
生存率中央値は、生存率0.5を意味する。
生存率0.5になるまでの時間を生存時間中央値(Median survival time, t とする)と呼ぶ。
$$ 0.5 = (1 – r)^t $$
生存時間中央値 (t) は、上記の式の両辺とも自然対数を取り、式展開すれば求められる。
$$ \log(0.5) = t \log(1 – r) $$
$$ t = \frac{\log(0.5)}{\log(1 – r)} $$
これで、5年生存率から生存期間中央値を逆算で求められた。
実例をもとに 5 年生存率から生存期間中央値を逆算で求める例
生存期間中央値を5年生存率から逆算で求める例題は、全がん協の生存率データを使ってみる。
https://www.zengankyo.ncc.go.jp/etc/seizonritsu/seizonritsu2010.html
生存率データから、代表的ながん、胃がん、大腸がん、乳がん、肺がん、肝がん、膵がんの第IV期の相対生存率を使って、生存期間中央値を逆算してみる。
胃がん 6.9%、大腸がん 22.0%、乳がん 38.5%、肺がん 4.9%、肝がん 1.7%、膵がん 1.5%である。
R で計算するスクリプトは以下の通り。
R.pct <- c(6.9,22.0,38.5,4.9,1.7,1.5)
cancer.name <- c("Stomach","Colorectal","Breast","Lung","Liver","Pancreas")
names(R.pct) <- cancer.name
R.pct
R.pctというベクトルに格納した。
> R.pct
Stomach Colorectal Breast Lung Liver Pancreas
6.9 22.0 38.5 4.9 1.7 1.5
5 年生存率から年間死亡率を逆算する。
R <- R.pct/100
r <- 1-R^(1/5)
round(r*100,1)
年間死亡率は以下の通り。
一番低いのは乳がんで17.4%、一番高いのは膵がん 56.8%。
> round(r*100,1)
Stomach Colorectal Breast Lung Liver Pancreas
41.4 26.1 17.4 45.3 55.7 56.8
年間死亡率から、生存期間中央値を逆算する。
t <- log(0.5)/log(1-r)
round(t,2)
年間死亡率が高ければ、生存期間中央値は短くなる。
一番短いのは、年間死亡率が最も高い膵がんで、0.83年。
> round(t,2)
Stomach Colorectal Breast Lung Liver Pancreas
1.30 2.29 3.63 1.15 0.85 0.83
検算してみる。
5年と生存期間中央値で、生存率がどうなるかの計算だ。
(1-r)^5
(1-r)^t
5年生存率は、データとしてウェブサイトの表から抽出した値に戻った。
100倍すればパーセントと同じになる。
また、生存期間中央値のべき乗は、すべて0.5となった。
間違いなく計算出来ている。
> (1-r)^5
Stomach Colorectal Breast Lung Liver Pancreas
0.069 0.220 0.385 0.049 0.017 0.015
> (1-r)^t
Stomach Colorectal Breast Lung Liver Pancreas
0.5 0.5 0.5 0.5 0.5 0.5
生存期間中央値を示したグラフを書いてみる
年間死亡率が計算できたところで、指数関数と考えて、グラフに描いてみる。
時間ゼロから、5年までを100分割する。
x <- 0:500/100
summary(x)
中央値が2.5年であることを確認する。
> summary(x)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 1.25 2.50 2.50 3.75 5.00
六つのがん種、5年間分の座標を格納するデータフレームを用意する。
全部ゼロが割り当てられる。
sr <- data.frame(matrix(rep(numeric(501),6),nc=6))
colnames(sr) <- cancer.name
str(sr)
srの内容は以下の通り。
> str(sr)
'data.frame': 501 obs. of 6 variables:
$ Stomach : num 0 0 0 0 0 0 0 0 0 0 ...
$ Colorectal: num 0 0 0 0 0 0 0 0 0 0 ...
$ Breast : num 0 0 0 0 0 0 0 0 0 0 ...
$ LungAdeno : num 0 0 0 0 0 0 0 0 0 0 ...
$ Liver : num 0 0 0 0 0 0 0 0 0 0 ...
$ Pancreas : num 0 0 0 0 0 0 0 0 0 0 ...
年間死亡率 r と観察時点 x を使って、観察時点の生存率を計算して、sr データフレームに格納していく。
for(i in 1:6){
sr[,i] <- (1-r[i])^x
}
str(sr)
summary(sr)
計算されて格納されたデータは以下の通り。
> str(sr)
'data.frame': 501 obs. of 6 variables:
$ Stomach : num 1 0.995 0.989 0.984 0.979 ...
$ Colorectal: num 1 0.997 0.994 0.991 0.988 ...
$ Breast : num 1 0.998 0.996 0.994 0.992 ...
$ Lung : num 1 0.994 0.988 0.982 0.976 ...
$ Liver : num 1 0.992 0.984 0.976 0.968 ...
$ Pancreas : num 1 0.992 0.983 0.975 0.967 ...
> summary(sr)
Stomach Colorectal Breast Lung
Min. :0.0690 Min. :0.2200 Min. :0.3850 Min. :0.0490
1st Qu.:0.1346 1st Qu.:0.3212 1st Qu.:0.4888 1st Qu.:0.1041
Median :0.2627 Median :0.4690 Median :0.6205 Median :0.2214
Mean :0.3486 Mean :0.5153 Mean :0.6444 Mean :0.3157
3rd Qu.:0.5125 3rd Qu.:0.6849 3rd Qu.:0.7877 3rd Qu.:0.4705
Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
Liver Pancreas
Min. :0.01700 Min. :0.01500
1st Qu.:0.04708 1st Qu.:0.04286
Median :0.13038 Median :0.12247
Mean :0.24179 Mean :0.23509
3rd Qu.:0.36109 3rd Qu.:0.34996
Max. :1.00000 Max. :1.00000
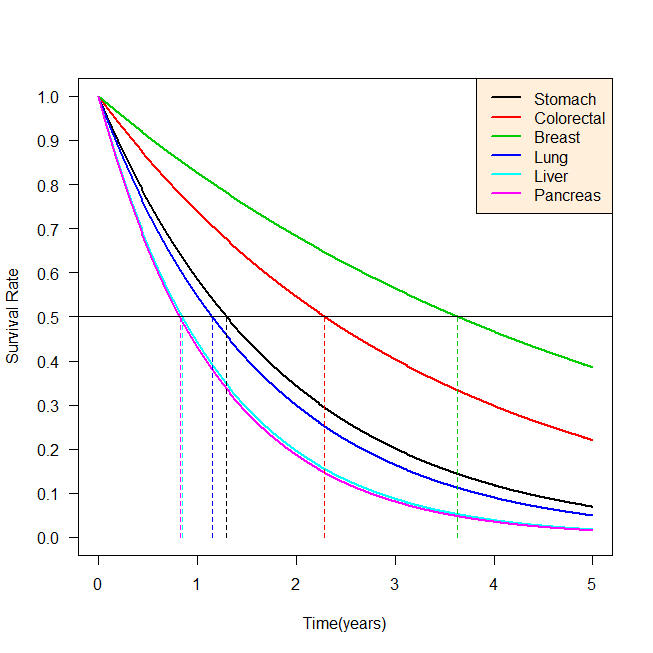
データをグラフに描く。
まず最初のがん種でplot()して、そのほかのがん種は、lines()で描きこむという方法を取っている。
abline()で、Y軸0.5のところに水平線を引いた。
これが生存率中央値である。
それぞれのグラフの線とY軸0.5の水平線が交わる点が、生存期間中央値で、それぞれ垂直線を破線で入れた。
with(sr,plot(x,sr[,1],ylim=c(0,1),las=1,ylab="Survival Rate",xlab="Time(years)",type="l",lwd=2,col=1,yaxp=c(0,1,10)))
for(i in 2:6){
with(sr,lines(x,sr[,i],lwd=2,col=i))
}
abline(h=0.5)
for(i in 1:6){
arrows(t[i],0,t[i],0.5,length=0,lty=2,col=i)
}
op <- par(bg = "antiquewhite1")
legend("topright",cancer.name,col=1:6,lwd=2)
par(op)
出来上がりはこちら。
まとめ
生存期間中央値を5年生存率から逆算で求める方法をまとめた。
がんの臨床試験・臨床研究の論文には通常、生存期間中央値と5年生存率の両方が掲載されていることがほとんであるが、どちらかしかない場合もある。
そういう場合に使える方法だ。
また、観察期間が短く5年まで到達していないこともある。
そんな場合にも応用可能だ。
エクセルで生存期間中央値計算
エクセルで生存期間中央値を計算するプログラムを作成した。
また、生存期間から生存率を計算するプログラムも作成した。
生存期間中央値のデータがあれば、5年生存率を予測することができるということだ。
エクセルファイルのイメージは以下の通り。

黒枠の値を変更すると、黄色ハイライトの数値が変わる。
黄色ハイライトセルの数値が求める数値だ。
もしよろしければ。









コメント