研究論文やデータ分析でよく耳にする「媒介効果」と「調整効果」。どちらも変数間の関係性を深く掘り下げる際に重要な概念であるが、その意味するところは大きく異なる。本記事では、これら二つの効果の違いを明確にし、具体的な例とRでの計算例を交えながら、それぞれの解釈方法までをわかりやすく解説する。自身のデータ分析の精度を一段と高めるために、ぜひ最後まで読んでほしい。
概要:媒介効果と調整効果の違い
- 媒介効果(Mediator Effect)とは、ある独立変数(X)が従属変数(Y)に影響を与える際に、その間に別の変数(M)が介在し、XからYへの影響がMを介して生じる関係性のことである。MはXとYの関係を「媒介する」役割を果たす。つまり、「XがMを引き起こし、MがYを引き起こす」という因果の連鎖を考える。
- 調整効果(Moderator Effect)とは、ある独立変数(X)が従属変数(Y)に与える影響の強さや方向が、別の変数(W)の値によって変化する関係性のことである。WはXとYの関係を「調整する」役割を果たす。つまり、「XとYの関係性はWの値によって異なる」という交互作用を考える。
| 特徴 | 媒介効果(Mediator) | 調整効果(Moderator) |
| 役割 | 独立変数と従属変数の関係を「媒介」する | 独立変数と従属変数の関係を「調整」する |
| 関係性 | X → M → Y (因果の連鎖) | (X → Y)← W (交互作用) |
| 問いかけ | なぜXはYに影響を与えるのか? | いつ(または誰にとって)XはYに影響を与えるのか? |
具体例
媒介効果の例:
- 「学習時間(X)」が「試験成績(Y)」に与える影響は、「理解度(M)」によって媒介される。
- 学習時間が増えるほど理解度が上がり、理解度が上がるほど試験成績が向上するという関係性である。学習時間自体が直接的に試験成績を上げるのではなく、理解度を介して影響を与えると考えられる。
調整効果の例:
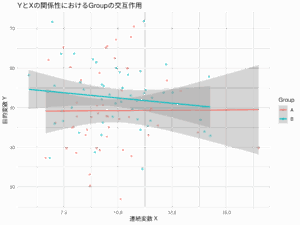
- 「新しい学習方法の導入(X)」が「試験成績(Y)」に与える影響は、「元々の学力レベル(W)」によって調整される。
- 新しい学習方法が、元々の学力が低い生徒には大きな効果をもたらすが、元々の学力が高い生徒にはあまり効果がない、あるいは逆効果になる場合も考えられる。この場合、元々の学力レベルが学習方法と試験成績の関係性を調整している。
R 計算例
ここでは、先ほどの例を参考に、Rを用いた簡略な計算例を示す。実際の分析では、さらに厳密なモデル選択や仮定の確認が必要である。
媒介効果のRでの計算例(lavaanパッケージを使用)
学習時間、理解度、試験成績の架空データを作成する。
R スクリプト例:
# パッケージのインストール(初回のみ)
# install.packages("lavaan")
# 必要なパッケージの読み込み
library(lavaan)
# 架空データの作成
set.seed(123)
data_mediation <- data.frame(
learning_time = round(rnorm(100, 10, 2)), # 学習時間
understanding = round(rnorm(100, 50, 10) + 2 * rnorm(100, 10, 2)), # 理解度(学習時間に影響される)
exam_score = round(rnorm(100, 70, 15) + 0.5 * rnorm(100, 50, 10)) # 試験成績(理解度に影響される)
)
# 媒介モデルの指定
mediation_model <- '
# 回帰パス
understanding ~ a * learning_time
exam_score ~ b * understanding + c * learning_time
# 間接効果(媒介効果)の計算
indirect := a * b
# 全効果の計算
total := c + (a * b)
'
# モデルの実行
fit_mediation <- sem(mediation_model, data = data_mediation)
# 結果の要約
summary(fit_mediation, standardized = TRUE, fit.measures = TRUE)
実行結果:
> summary(fit_mediation, standardized = TRUE, fit.measures = TRUE)
lavaan 0.6-19 ended normally after 1 iteration
Estimator ML
Optimization method NLMINB
Number of model parameters 5
Number of observations 100
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Model Test Baseline Model:
Test statistic 1.494
Degrees of freedom 3
P-value 0.684
User Model versus Baseline Model:
Comparative Fit Index (CFI) 1.000
Tucker-Lewis Index (TLI) 1.000
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -795.795
Loglikelihood unrestricted model (H1) -795.795
Akaike (AIC) 1601.590
Bayesian (BIC) 1614.616
Sample-size adjusted Bayesian (SABIC) 1598.825
Root Mean Square Error of Approximation:
RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.000
P-value H_0: RMSEA <= 0.050 NA
P-value H_0: RMSEA >= 0.080 NA
Standardized Root Mean Square Residual:
SRMR 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
understanding ~
learnng_tm (a) -0.384 0.577 -0.665 0.506 -0.384 -0.066
exam_score ~
undrstndng (b) -0.036 0.155 -0.233 0.816 -0.036 -0.023
learnng_tm (c) -0.909 0.895 -1.015 0.310 -0.909 -0.101
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.understanding 108.204 15.302 7.071 0.000 108.204 0.996
.exam_score 258.821 36.603 7.071 0.000 258.821 0.990
Defined Parameters:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
indirect 0.014 0.063 0.220 0.826 0.014 0.002
total -0.895 0.893 -1.002 0.316 -0.895 -0.100
> 調整効果のRでの計算例(標準的な回帰分析を使用)
新しい学習方法の導入、試験成績、元々の学力レベルの架空データを作成する。
R スクリプト例:
# 架空データの作成
set.seed(456)
data_moderation <- data.frame(
new_method = sample(0:1, 100, replace = TRUE), # 新しい学習方法の導入(0:なし, 1:あり)
initial_ability = round(rnorm(100, 60, 10)) # 元々の学力レベル
)
# 試験成績(新しい学習方法と初期学力の交互作用を考慮)
data_moderation$exam_score <-
round(70 + 5 * data_moderation$new_method + 0.3 * data_moderation$initial_ability +
-0.2 * data_moderation$new_method * data_moderation$initial_ability + rnorm(100, 0, 5))
# 調整効果(交互作用項)を含む回帰モデルの指定
# I()で交互作用項を明示的に指定
moderation_model <- lm(exam_score ~ new_method * initial_ability, data = data_moderation)
# モデルの要約
summary(moderation_model)
実行結果:
> summary(moderation_model)
Call:
lm(formula = exam_score ~ new_method * initial_ability, data = data_moderation)
Residuals:
Min 1Q Median 3Q Max
-11.742 -3.504 0.420 3.554 10.212
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 66.72526 4.63566 14.394 < 2e-16 ***
new_method 8.97447 6.29060 1.427 0.15693
initial_ability 0.36660 0.07679 4.774 6.46e-06 ***
new_method:initial_ability -0.28576 0.10390 -2.750 0.00712 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.922 on 96 degrees of freedom
Multiple R-squared: 0.4874, Adjusted R-squared: 0.4714
F-statistic: 30.43 on 3 and 96 DF, p-value: 6.514e-14
> 結果解釈
媒介効果の解釈:
lavaanパッケージの出力では、以下の点に注目する。
aパス(独立変数 → 媒介変数)の有意性: 学習時間が理解度に有意な影響を与えているか。bパス(媒介変数 → 従属変数)の有意性: 理解度が試験成績に有意な影響を与えているか。cパス(独立変数 → 従属変数)の有意性(直接効果): 理解度を統制した上で、学習時間が試験成績に直接的な影響を与えているか。indirect(間接効果)の有意性: 媒介効果が存在するかどうかを示す。これが有意であれば、学習時間が理解度を介して試験成績に影響を与えていると言える。total(全効果): 媒介効果と直接効果を合わせた独立変数から従属変数への全体の影響である。
もし間接効果が有意で、直接効果が有意でなければ「完全媒介」、直接効果も有意であれば「部分媒介」と解釈される。
調整効果の解釈:
回帰分析の出力では、new_method:initial_abilityと出力されている、交互作用項に注目する。
- 交互作用項の係数とp値: この係数が有意であれば、調整効果が存在すると判断できる。
- 係数が正の場合:
initial_abilityが高いほど、new_methodがexam_scoreに与える正の影響が強まる、または負の影響が弱まる。 - 係数が負の場合:
initial_abilityが高いほど、new_methodがexam_scoreに与える正の影響が弱まる、または負の影響が強まる。
- 係数が正の場合:
この例では、new_methodとinitial_abilityの交互作用項の係数とp値を見ることで、元々の学力レベルが新しい学習方法の試験成績への効果をどのように調整しているかを判断する。例えば、交互作用項が負で有意であれば、「元々の学力レベルが高いほど、新しい学習方法の効果は小さくなる」と解釈できる。
まとめ
媒介効果と調整効果は、変数間の関係性を深く理解するための強力なツールである。媒介効果は「なぜ」ある影響が生じるのかというメカニズムを、調整効果は「いつ」「どのような条件下で」ある影響が生じるのかという状況を明らかにする。これらの概念を適切に使い分けることで、より精緻なデータ分析が可能となり、研究やビジネスにおける意思決定に貢献できるであろう。ぜひ自身のデータでこれらの分析を試してみてほしい。





コメント