統計解析において、欠測データは常に悩ましい問題である。特に、欠測がランダムではない(Missing Not At Random; MNAR)場合、多重代入(Multiple Imputation; MI)のような標準的な対処法を用いても、推定値にバイアスが生じる可能性がある。
本記事では、mice パッケージで多重代入を行ったデータに対して、MNARを仮定した感度分析を行う方法について解説する。見えない欠測が結果に与える影響を評価し、よりロバストな結論を導き出すための実践的なアプローチを探る。
MNARの概要
MNAR(Missing Not At Random)とは、欠測メカニズムの一種で、データが欠測しているかどうか、あるいは欠測値そのものが、欠測している値に依存している状態を指す。例えば、ある質問への回答が「回答しにくい」という理由で欠測している場合などがこれに該当する。MNARの欠測は観測データからそのメカ測ニズムを特定することが困難であり、標準的な多重代入法(Missing At Random; MARを仮定)ではバイアスを完全に除去することはできない。
MNARを仮定したときの感度分析の代表例
MNARを仮定した感度分析は、仮定するMNARメカニズムを変化させながら、分析結果がどのように変化するかを評価する手法である。これにより、MNARの存在が結論に与える影響の大きさを把握できる。代表的な感度分析の例としては、以下のようなものがある。
- 選択バイアスモデル (Selection Bias Model): 欠測メカニズムをモデル化し、そのパラメータを変化させることで感度分析を行う。例えば、プロビットモデルやロジットモデルを用いて、欠測の確率をモデル化する。
- パターン混合モデル (Pattern-Mixture Model): 欠測パターンごとに異なるモデルを仮定し、それぞれのモデルで代入を行う。
- デルタ調整法 (Delta Adjustment Method): 代入時に、観測されている値と欠測値の間の差(デルタ)を仮定し、そのデルタの値を変化させることで感度分析を行う。これは比較的シンプルで直感的な方法である。
具体例
ここでは、デルタ調整法でmiceを用いたMNAR感度分析を具体的に見ていこう。
シナリオ: ある疾患の治療効果を評価する臨床試験において、患者のQOLスコア(Quality of Life score)を測定した。しかし、QOLスコアが高い(改善した)患者ほど、フォローアップ調査への回答率が低い、というMNARの可能性が疑われている。つまり、QOLスコアの欠測は、そのQOLスコア自体に依存しているかもしれない。
目的: このMNARの可能性を考慮し、治療効果の推定値がどの程度ロバストであるかを評価する。
データ:
treatment: 治療群(0: 対照群, 1: 介入群)qol_baseline: ベースラインQOLスコアqol_followup: フォローアップQOLスコア(欠測あり)age: 年齢sex: 性別
ここでは、qol_followup にMNARを仮定する。具体的には、「qol_followup の真の値が高いほど、欠測しやすい」というシナリオを考える。miceパッケージの感度分析では、代入される値にオフセット(デルタ)を加えることで、この仮定を表現する。
具体例のRでの解析
以下のスクリプトではカスタム代入関数を定義して、デルタ調整を行っている。標準の mice.impute.norm をベースに、欠測値(のみ)に delta を加算する関数 mice.impute.my.deltaを作成している。
R 計算例:
if(!require(mice)) install.packages("mice")
if(!require(dplyr)) install.packages("dplyr")
library(mice)
library(dplyr)
# サンプルデータの作成(MNARを模擬)
set.seed(123)
n <- 200
data <- data.frame(
treatment = sample(0:1, n, replace = TRUE),
qol_baseline = round(rnorm(n, 70, 10)),
age = round(rnorm(n, 50, 10)),
sex = sample(c("Male", "Female"), n, replace = TRUE, prob = c(0.4, 0.6))
)
# qol_followup を作成し、意図的にMNARを発生させる
data$qol_followup <- data$qol_baseline + round(rnorm(n, 5, 5))
# QOLが高いほど欠測しやすいように調整
data$missing_prob <- plogis((data$qol_followup - 75) / 10) # QOLが高いほど欠測確率を上げる
data$qol_followup[runif(n) < data$missing_prob] <- NA
# データフレームの確認
summary(data)
str(data)
data$missing_prob <- NULL # 欠測を作成した確率値は削除しておく
# 1. MARを仮定した多重代入 (標準的な MICE)
ini <- mice(data, maxit = 0) # 初期設定
meth_ini <- ini$method
meth_ini["qol_followup"] <- "norm"
# 多重代入の実行 (m=5)
imputed_data_mar <- mice(data, m = 5, method = meth_ini, seed = 123)
# 2. MNARを仮定した感度分析 (デルタ調整)
ini_mnar <- mice(data, maxit = 0)
# 1. カスタム代入関数の定義
# 標準の mice.impute.norm をベースに、欠測値(のみ)に delta を加算する関数
mice.impute.my.delta <- function(y, ry, x, wy = NULL, ...) {
# 通常の正規分布モデル(MAR仮定)で暫定的な代入値を生成
imp <- mice.impute.norm(y, ry, x, wy = wy, ...)
# 生成された代入値に delta (オフセット) を加える
# これにより MNAR (非ランダムな欠測) をシミュレートする
return(imp + delta_val)
}
# 2. シミュレーションの実行 (ご提示のループ部分の修正版)
results_mnar <- list()
deltas <- c(0, 2, 5, 8)
for (d in deltas) {
delta_val <<- d
# メソッドの指定
meth_mnar <- ini_mnar$method
meth_mnar["qol_followup"] <- "my.delta" # 自作関数を指定
# 多重代入の実行
imputed_data_mnar <- mice(
data,
m = 5,
method = meth_mnar,
printFlag = FALSE,
seed = 123
)
# 解析とプーリング
fit_mnar <- with(imputed_data_mnar, lm(qol_followup ~ treatment + qol_baseline + age + sex))
results_mnar[[as.character(d)]] <- pool(fit_mnar)
}
# 結果の表示
for (d in names(results_mnar)) {
cat("\n--- Delta =", d, " (MNAR Adjustment) ---\n")
print(summary(results_mnar[[d]]))
}
# MARの結果と比較
cat("\n--- MAR Result (Delta = 0) ---\n")
fit_mar <- with(imputed_data_mar, lm(qol_followup ~ treatment + qol_baseline + age + sex))
pooled_fit_mar <- pool(fit_mar)
print(summary(pooled_fit_mar))結果解釈
上記のRコードを実行すると、異なる delta 値(0, 2, 5, 8)で分析を行った結果が出力される。
> # 結果の表示
> for (d in names(results_mnar)) {
+ cat("\n--- Delta =", d, " (MNAR Adjustment) ---\n")
+ print(summary(results_mnar[[d]]))
+ }
--- Delta = 0 (MNAR Adjustment) ---
term estimate std.error statistic df p.value
1 (Intercept) 2.63392725 5.44319238 0.4838938 8.168233 6.411680e-01
2 treatment 0.53426485 0.89486417 0.5970346 24.176959 5.560348e-01
3 qol_baseline 1.05741561 0.06524959 16.2057058 7.574072 3.750016e-07
4 age -0.04870436 0.04653048 -1.0467195 17.981612 3.090959e-01
5 sexMale -0.31366516 0.88395565 -0.3548426 35.046615 7.248340e-01
--- Delta = 2 (MNAR Adjustment) ---
term estimate std.error statistic df p.value
1 (Intercept) 0.96596817 5.46990274 0.1765970 8.328498 8.640441e-01
2 treatment 0.56534053 0.90294630 0.6261065 24.933889 5.369352e-01
3 qol_baseline 1.09345289 0.06554641 16.6821173 7.713705 2.495390e-07
4 age -0.04867688 0.04690672 -1.0377378 18.508527 3.127604e-01
5 sexMale -0.29134230 0.89285311 -0.3263049 36.178271 7.460739e-01
--- Delta = 5 (MNAR Adjustment) ---
term estimate std.error statistic df p.value
1 (Intercept) -1.53597045 5.63211769 -0.2727163 9.341514 7.910043e-01
2 treatment 0.61195405 0.95135836 0.6432424 29.723701 5.249987e-01
3 qol_baseline 1.14750882 0.06735125 17.0376759 8.594078 6.373378e-08
4 age -0.04863566 0.04916743 -0.9891844 21.861665 3.333956e-01
5 sexMale -0.25785802 0.94596994 -0.2725859 43.234480 7.864693e-01
--- Delta = 8 (MNAR Adjustment) ---
term estimate std.error statistic df p.value
1 (Intercept) -4.03790908 5.92942436 -0.6809951 11.38449 5.094891e-01
2 treatment 0.65856757 1.03750858 0.6347587 39.23541 5.292701e-01
3 qol_baseline 1.20156476 0.07066824 17.0028957 10.36146 6.630430e-09
4 age -0.04859443 0.05321642 -0.9131473 28.64594 3.687870e-01
5 sexMale -0.22437374 1.03984718 -0.2157757 56.67338 8.299373e-01
> # MARの結果と比較
> cat("\n--- MAR Result (Delta = 0) ---\n")
--- MAR Result (Delta = 0) ---
> fit_mar <- with(imputed_data_mar, lm(qol_followup ~ treatment + qol_baseline + age + sex))
> pooled_fit_mar <- pool(fit_mar)
> print(summary(pooled_fit_mar))
term estimate std.error statistic df p.value
1 (Intercept) 2.63392725 5.44319238 0.4838938 8.168233 6.411680e-01
2 treatment 0.53426485 0.89486417 0.5970346 24.176959 5.560348e-01
3 qol_baseline 1.05741561 0.06524959 16.2057058 7.574072 3.750016e-07
4 age -0.04870436 0.04653048 -1.0467195 17.981612 3.090959e-01
5 sexMale -0.31366516 0.88395565 -0.3548426 35.046615 7.248340e-01delta = 0の結果: これはMARを仮定した場合の結果と同一である。例えば、treatmentの係数(治療効果)が有意であるかどうか、その効果量などを確認する。delta = 2, 5, 8の結果:deltaの値が大きくなるにつれて(つまり、欠測しているQOLがより高いと仮定するにつれて)、treatmentの係数やその有意性がどのように変化するかを観察する。
結果解釈のポイント:
- 係数の変化:
treatmentの係数がdeltaの増加とともに増加しているが、大きな差異はない。 - 標準誤差の変化: 係数だけでなく、標準誤差やp値の変化も重要である。標準誤差が大きくなると、信頼区間が広がり、結論の不確実性が増す。今回の例では、大きな差異はない。
- 結論のロバスト性:
deltaの値が現実的に考えられる範囲で変化しても、主要な結論(例:治療効果の有無、方向性)が変わらない場合、その結論はMNARに対して比較的ロバストであると言える。下記の図でも確認できる。 - 感度が高い場合: 特定の
deltaの仮定で結果が大きく変化する場合、MNARの存在が結論に深刻な影響を与える可能性があることを意味する。この場合、研究者はその不確実性を明確に示し、結果の解釈に慎重になる必要がある。
結果の可視化
上記結果を treatment の偏回帰係数が delta によって異なるのかどうかを示す図を作成する。
# MAR + MNAR visualization
# 1. MARの結果をデータフレーム化
summ_mar <- summary(pooled_fit_mar, conf.int = TRUE)
target_mar <- summ_mar[summ_mar$term == "treatment", ]
mar_plot_data <- data.frame(
type = "MAR (Standard)",
delta = -1, # グラフ上で左側に配置するためのダミー値
estimate = target_mar$estimate,
std.error = target_mar$std.error,
conf.low = target_mar$`2.5 %`,
conf.high = target_mar$`97.5 %`
)
# 2. MNARの結果をデータフレーム化
mnar_plot_data <- data.frame()
for (d in names(results_mnar)) {
summ <- summary(results_mnar[[d]], conf.int = TRUE)
target <- summ[summ$term == "treatment", ]
mnar_plot_data <- rbind(mnar_plot_data, data.frame(
type = "MNAR (Delta-adjusted)",
delta = as.numeric(d),
estimate = target$estimate,
std.error = target$std.error,
conf.low = target$`2.5 %`,
conf.high = target$`97.5 %`
))
}
# 3. データの結合
final_plot_data <- rbind(mar_plot_data, mnar_plot_data)
# 4. 可視化
ggplot(final_plot_data, aes(x = delta, y = estimate, color = type)) +
geom_point(size = 3) +
geom_errorbar(aes(ymin = conf.low, ymax = conf.high), width = 0.3) +
# MNARの点だけを線で結ぶ
geom_line(data = subset(final_plot_data, type == "MNAR (Delta-adjusted)"),
aes(x = delta, y = estimate), size = 1) +
geom_hline(yintercept = 0, linetype = "dashed", color = "black") +
# x軸のラベルを調整(-1 の位置を "MAR" と表示)
scale_x_continuous(breaks = c(-1, 0, 2, 5, 8),
labels = c("MAR", "0", "2", "5", "8")) +
labs(
title = "Comparison of Treatment Effects: MAR vs MNAR",
subtitle = "Sensitivity analysis showing robustness of treatment estimates",
x = "Assumed Delta (MNAR) compared to standard MAR",
y = "Treatment Effect Estimate (95% CI)",
color = "Model Type"
) +
theme_minimal() +
theme(legend.position = "bottom")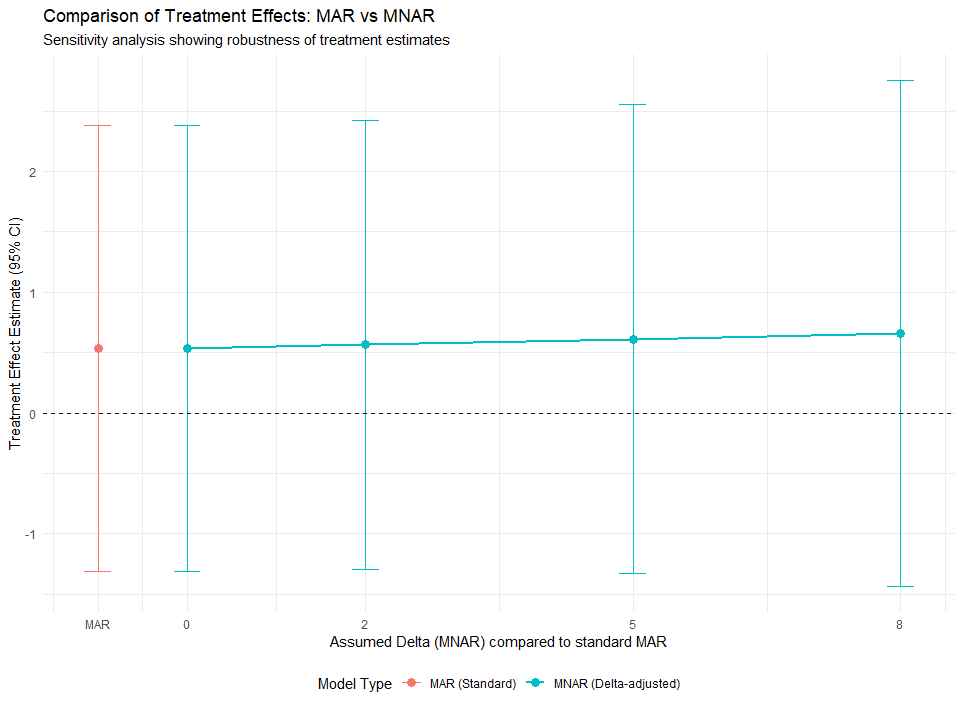
図は、MAR と MNAR delta=0 が同じ偏回帰係数の推定値であることを示しており、delta が 2, 5, 8 と大きくなるにつれ、若干点推定値は大きくなるも、大きな変化はなかったことがわかる。
この結果、MNAR を想定して、qol_followup が大きい症例が脱落しやすかったと仮定した場合でも、結果に大きな違いはなく、結論は、欠測がMARと想定した多重代入であっても問題なかったと言える。
まとめ
miceを用いた多重代入におけるMNAR感度分析は、欠測データがMNARである可能性を考慮し、分析結果のロバスト性を評価するための強力なツールである。特に、上記のように、欠測値と観測値の間に仮定される差(デルタ)を変化させるデルタ調整法は、比較的直感的に感度分析を行うことができる。
この感度分析を通じて、我々は単に「欠測に対処した」というだけでなく、「欠測メカニズムの不確実性が結果にどの程度影響するか」という重要な問いに答えることができる。これにより、より透明性の高い、信頼性の高い研究結果の報告が可能となり、ひいては科学的知見の確実性を高めることに繋がる。欠測データの多い研究においては、積極的にMNAR感度分析を検討することをお勧めする。





コメント