R でノンパラメトリック検定の多重比較を実行する方法

ノンパラメトリックの多重比較をRで実施する方法。

ノンパラメトリックとは何か？

ノンパラメトリックとはパラメトリックではないという意味。

パラメトリックとは、パラメーターを使うという意味だ。

パラメーターとは、日本語では母数（ぼすう）と言われて、母集団を表す数値、例えば母平均、母分散などを指す。

たとえばTukey検定やDunnett検定は、母平均、母分散の前提の下、実施される多重比較検定だ。

また、Welchの方法で二群比較を繰り返して、Bonferroni型のp値調整を行う多重比較も、Welchの方法がパラメトリックなので、パラメトリック検定だ。

母平均、母分散が前提ではない方法が、ノンパラメトリック検定だ。

ノンパラメトリックの多重比較とは？

一般的な方法

二群のノンパラメトリック検定の代表格は、Wilcoxon ウィルコクソン順位和検定だ。

Mann-Whitney マン・ホイットニーのU検定とも言う。

多重比較は二群比較を繰り返し、Bonferroni型のp値調整を行う。

Bonferroni型のp値調整とは？

Rには、pairwise.wilcox.test()という関数が準備されている。

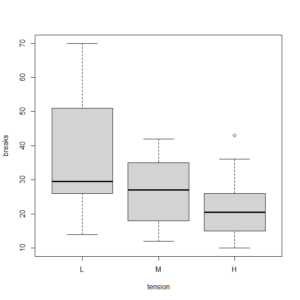
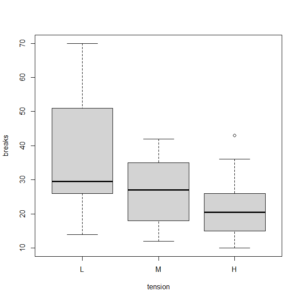
たとえば、warpbreaksというデータを使って、tensionの高さによってbreaksの数に違いがあるか検定をしてみる。

warpbreaksの説明は以下の記事参照（文中に簡単な説明あり）

Wilcoxonの順位和検定を三回繰り返し、Holmの方法でp値を調整している。

結果の最後のエラーが出ている。

同順位があって正確に計算できていないということだ。

同順位がある場合は正確確率法が望ましい。

> with(warpbreaks, (pairwise.wilcox.test(breaks, tension)))
Pairwise comparisons using Wilcoxon rank sum test
data:  breaks and tension
  L      M
M 0.1470 -
H 0.0052 0.1470
P value adjustment method: holm
Warning messages:
1: In wilcox.test.default(xi, xj, paired = paired, ...) :
cannot compute exact p-value with ties
2: In wilcox.test.default(xi, xj, paired = paired, ...) :
cannot compute exact p-value with ties
3: In wilcox.test.default(xi, xj, paired = paired, ...) :
cannot compute exact p-value with ties

正確確率を用いた方法

同順位がある場合の不正確さを乗り越えるために、正確確率検定 Exact Testを用いる。

また、Exact Testは、等分散性を仮定しなくてもいいので適応範囲が広く、その点でもより適切な方法だ。

Wilcoxon Exact Testは、coinパッケージをインストールして、wilcox_test()という関数で実施する。

インストールは最初の一回だけだ。

install.packages("coin")

追加したパッケージは、使う時に呼び出す必要がある。

library(coin)

pairwise.wilcox.test()のように自動で全ペアを計算してくれないので、手動で三回検定を行う必要がある。

warpbreaksから、tensionのH抜き、L抜き、M抜きの三つのデータセットを作り、それぞれwilcox_coin()で検定する。

distribution=”exact”が正確確率検定の指定だ。

結果は、

LとH： p = 0.001147

LとM：p = 0.07194

MとH：p = 0.08857

> warpbreaks.LM <- subset(warpbreaks, warpbreaks$tension!="H")
> warpbreaks.MH <- subset(warpbreaks, warpbreaks$tension!="L")
> warpbreaks.HL <- subset(warpbreaks, warpbreaks$tension!="M")
> wilcox_test(breaks~tension, data=warpbreaks.LM, distribution="exact")
Exact Wilcoxon-Mann-Whitney Test
data:  breaks by tension (L, M)
Z = 1.8056, p-value = 0.07194
alternative hypothesis: true mu is not equal to 0
> wilcox_test(breaks~tension, data=warpbreaks.MH, distribution="exact")
Exact Wilcoxon-Mann-Whitney Test
data:  breaks by tension (M, H)
Z = 1.7117, p-value = 0.08857
alternative hypothesis: true mu is not equal to 0
> wilcox_test(breaks~tension, data=warpbreaks.HL, distribution="exact")
Exact Wilcoxon-Mann-Whitney Test
data:  breaks by tension (L, H)
Z = 3.1507, p-value = 0.001147
alternative hypothesis: true mu is not equal to 0

HolmとHochbergの方法で調整すると？

結論として、LとHだけが統計学的有意に異なるという結果だ。

下表の黄色ハイライトの部分。

Holmの方法

Holmの方法は、三つのp値のうちもっとも小さいp値からチェックしていく。

今回のように三ペアあるなら、もっとも小さいp値を3倍して0.05と比較する。

0.05より小さいので、第一段階突破！

次に大きいLとMのp値のチェックに移る。

LとMのp値は2倍して0.05と比較する。

0.05より大きくいので、ここでチェック終了。

Holmの方法では、LとHペアのみ統計学的有意。

Hochbergの方法

Hochbergの方法は、もっとも大きいp値からチェック開始。

もっとも大きいp値と0.05を比較する。

0.05より大きいので、次に移る。

次に大きいp値を2倍して0.05と比較する。

これも0.05より大きいので、もっとも小さいp値に移る。

もっとも小さいp値を3倍して0.05と比較する。

これは0.05より小さいので、このペアは統計学的有意に異なるといえる。

もし、もっと小さいp値のペアがある場合、もっと小さいp値はチェックなしで統計学的有意になる。

これがHochbergの方法だ。

今回は、結果としてHolmもHochbergも同じだった。

ペア	調整なし	Holm	Hochberg
LとH	0.001147	(1) \begin{array}{lcl} 0.00147 \times 3 \\ = 0.003441 \\ \lt 0.05 \end{array}	(3) \begin{array}{lcl} 0.001147 \times 3 \\ = 0.003441 \\ \lt 0.05 \end{array}
LとM	0.07194	(2) \begin{array}{lcl} 0.07194 \times 2 \\ = 0.14388 \\ \gt 0.05 \end{array}	(2) \begin{array}{lcl} 0.07194 \times 2 \\ = 0.14388 \\ \gt 0.05 \end{array}
MとH	0.08857		(1) \begin{array}{lcl} 0.08857 \times 1 \\ = 0.08857 \\ \gt 0.05 \end{array}

まとめ

測定値のような数値データで、三群以上を多重比較したい場合、データが正規分布しているか不明なら、ノンパラメトリック検定を使うとよい。

適切な方法はWilcoxon Exact Testを繰り返して行い、Bonferroni型のp値調整を行う方法だ。

p値調整法は、HolmかHochbergがおすすめだが、検出力の高いHochbergの方法がよりおすすめだ。