検証試験において、三群以上の平均値を比較したいときに、単純に二群比較を繰り返すと有意水準が甘くなる。
有意水準の調整によって簡単に処理する方法がボンフェローニ (Bonferroni)の方法とその進化版だ。
Rでボンフェローニ型のP値調整で多重比較を行ってみた。
ボンフェローニの方法とは?
ボンフェローニの方法とは、比較のペア数で有意水準を割り、統計学的有意の基準を厳しくする方法。
三群を総当たりで比較すると三ペアできる。
- グループ1とグループ2
- グループ2とグループ3
- グループ3とグループ1
この三つだ。
二群であれば一回の計算で有意水準5%のところ、三回あるので0.05を3で割って0.0167を有意水準にするというのがボンフェローニの方法。
一見理屈が通っているのだけれど、基準が厳しくなりすぎている。
三ペアの比較は完全に独立ではない(少し関係ある)ので、全部のペアの水準を一律ペア数で割るのは厳しすぎる。
そこで考えられたのがボンフェローニの改良版だ。
ボンフェローニの改良版、ホルムの方法、ホックバーグの方法
ホルムの方法とは?
ホルム(Holm) はボンフェローニの厳しすぎる問題点を、だんだんに緩くしていく方法で解決する提案をした。
P値を小さい順にならべて、もっとも小さいp値は最も小さい有意水準と比較する。
だんだんに有意水準は大きくしていって、最終的には0.05と比較する。
例えば、三ペアの比較であれば、もっとも小さいp値を0.05÷3=0.0167と比較し、二番目に小さいp値は0.05÷2=0.025と比較する。最も大きいP値は0.05と比較する。
比較する水準よりも大きいp値になった時点で比較は終了する。
Rでは、例えば三ペアなら、もっとも小さいp値を3倍、次を2倍、最も大きいp値はそのままという風にして、すべてを0.05と比較する形式をとっている。
これがホルムの方法だ。
ホックバーグの方法とは?
ホックバーグ(Hochberg)の方法は、ホルムの方法よりも検出力が高い方法で、統計学的有意な差をよりよく検出してくれる。
ホルムの方法とは逆に、大きいp値から有意水準と比較していく。
たとえば三ペアあったとすると、一番大きいp値を0.05と比較し、二番目に大きいp値を0.05÷2=0.025と比較し、一番小さいp値を0.05÷3=0.0167と比較する。
どこかで有意水準を下回ったら、それ以上は比較しない。
つまり、一番大きいp値が0.05を下回ったら、それ以外はすべて統計学的有意とする。
逆に上回ったら、二番目のP値と0.05÷2と比較する。
二番目で0.025÷2より下回ったら、三番目を見ずして、二番目のペア、三番目のペアはともに有意として終了。
Rでは、大きいP値から1倍、2倍、3倍として、0.05と比較すればいいようになっている。
Rでボンフェローニ型のP値調整を実際にやってみる
Rで実際にやってみる。
warpbreaksというデータを使う。
以下でも使用している。
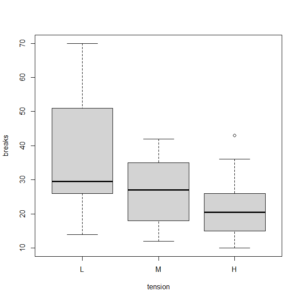
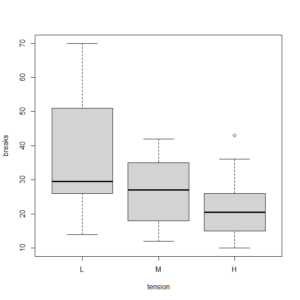
pairwise.t.test()という関数を使う。
等分散かどうかを気にしなくていいように、プールした分散を使わない設定で計算する。
分散をプールするには、分散が大体同じであるという前提が必要だ。
それを考えなくていいようにプールした分散を使わない設定でいく。
Rで二群比較の繰り返しをするとどうなる?
多重比較をする前に、二群比較を繰り返してやってみる。
pariwise.t.test()を使って、p値の調整をなしにすると、二群比較を繰り返した時のp値が計算される。
- LとHはp値 0.0023
- LとMはp値 0.0325
- HとMはp値 0.1146
LとM、LとHはともに有意水準5%で統計学的有意に見える。
> with(warpbreaks, (pairwise.t.test(breaks, tension, pool.sd=F, p.adj="none")))
Pairwise comparisons using t tests with non-pooled SD
data: breaks and tension
L M
M 0.0325 -
H 0.0023 0.1146
P value adjustment method: none
Rでボンフェローニの方法を行うとどうなるか?
すべてのp値が3倍されて出力されている。
LH間だけ有意となる。
- LとHはp値 $ 0.0023 \times 3 = 0.007 $
- LとMはp値 $ 0.0325 \times 3 = 0.098 $
- HとMはp値 $ 0.1146 \times 3 = 0.344 $
> with(warpbreaks, (pairwise.t.test(breaks, tension, pool.sd=F, p.adj="bonferroni")))
Pairwise comparisons using t tests with non-pooled SD
data: breaks and tension
L M
M 0.098 -
H 0.007 0.344
P value adjustment method: bonferroni
Rでホルムの方法を行うとどうなるか?
こちらもLH間だけ有意。
LH間だけが統計学的有意に異なるという結果になる。
LM間は0.05を上回ったので、この時点で有意水準との比較は終了。
しかし、ボンフェローニの方法よりもLM間は惜しい結果になる。
これがボンフェローニの方法ほど厳しくないゆえんだ。
- LとHはp値 3倍 $0.0023 \times 3 =0.007 $
- LとMはp値 2倍 $ 0.0325 \times 2 = 0.065 $
- HとMはp値 1倍 $ 0.1146 \times 1 = 0.1145 $
> with(warpbreaks, (pairwise.t.test(breaks, tension, pool.sd=F)))
Pairwise comparisons using t tests with non-pooled SD
data: breaks and tension
L M
M 0.065 -
H 0.007 0.115
P value adjustment method: holm
Rでホックバーグの方法を行うとどうなる?
HM間は0.05を上回っているので、次に大きいp値のLM間に移り、LM間のp値は2倍されて、0.05より大きいので、最後にLH間に移る。
LH間は3倍されても0.007で、初めて0.05を下回り、LH間だけが統計学的有意な差があるという結果になる。
- HとMはp値 1倍 $ 0.1146 \times 1 = 0.115 $
- LとMはp値 2倍 $ 0.0325 \times 2 = 0.065 $
- LとHはp値 3倍 $ 0.0023 \times 3 = 0.007 $
> with(warpbreaks, (pairwise.t.test(breaks, tension, pool.sd=F, p.adj="hochberg")))
Pairwise comparisons using t tests with non-pooled SD
data: breaks and tension
L M
M 0.065 -
H 0.007 0.115
P value adjustment method: hochberg
もしも三番目のp値が3倍すると0.05を超えてしまっていても、二番目のp値が2倍で0.05を下回っていれば、二番目、三番目のp値ともに統計学的有意になる。
この点がホックバーグの方法が検出力が高いゆえんだ。
まとめ
Rでボンフェローニi調整を行う方法を紹介した。
二群の比較をウェルチの方法で行い、
- 小さいp値にペア数をかけて、だんだん基準を緩めていくのがホルムの方法。
- 大きいp値からだんだん基準をきつくしていくのがホックバーグの方法。
ホルムより検出力が高いホックバーグの方法がおすすめ。
いずれの方法もRなら簡単にできる。
EZRで多重比較【無料統計ソフトEZRで簡単統計】【動画】
EZRなら、Rを簡単に使える。
参考書籍
丹後俊郎著 無作為化比較試験 朝倉書店
7 複数のエンドポイントの評価










コメント
コメント一覧 (5件)
[…] […]
[…] […]
[…] […]
[…] […]
[…] R でボンフェローニを実行する方法 […]