三群以上の平均値を多重比較したい。
でも各群の背景因子がそろっていない。
背景因子を調整しながら三群以上の平均値を多重比較するにはどうすればいいか？
R でのやり方を解説する。
目次
共変量を調整して多重比較する方法
群ごとの背景因子は、群分け変数と一緒に変わる量（変数）なので、共変量（きょうへんりょう）と呼ぶ。
共変量を調整しながら多重比較してみる。
共変量を調整しない多重比較は下記参照。
あわせて読みたい
R でチューキー検定を行う方法
Tukey HSD検定をRで行う方法の解説。 Tukey HSD検定をRで行う方法 aov()とTukeyHSD()という二つの関数を使う。 ダネット検定のときと同じように、例としてwarpbreaksと…
あわせて読みたい
R でダネット検定を行う方法
ダネット検定は、比較対照群といくつかの実験群を多重比較する方法。 Rでダネット検定をするにはどうしたらよいか？ Rでダネット検定をするには？ まずmultcompパッケー…
使用するデータ
今回例に使うのはmultcompパッケージのlitterというデータ。
生まれた仔ラット全体の体重を四つの用量群で比較する。
共変量は、出産までの妊娠日数と生まれた仔ラットの数。
library(multcomp)
summary(litter)
boxplot(weight ~ dose, data=litter, xlab="Dose", ylab="Weight")
summary(aov(weight ~ dose, data=litter))
round(cor(litter[,-1]),3)
summary(aov(gesttime ~ dose, data=litter))
summary(aov(number ~ dose, data=litter))
データの概要：
- 処置用量は0、５、50、500の四群。17例から20例。
- 仔ラット全体の体重の平均は30.33グラム。
- 妊娠期間は、平均22.09日。
- 平均仔ラット数は13.43匹。
下記は処置用量と体重の箱ひげ図。
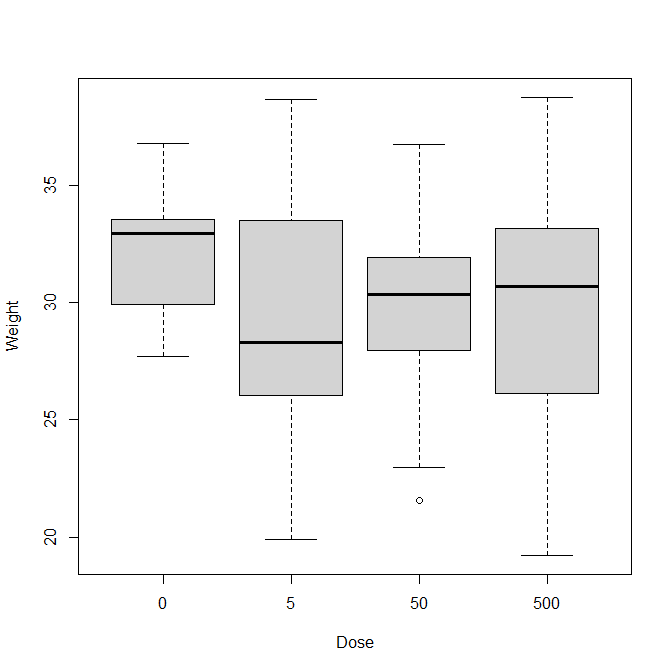
また、ANOVAや相関係数など単変量解析では、どの変数間にも強い関連性は見られないことがわかる。
> library(multcomp)
>
> summary(litter)
dose weight gesttime number
0 :20 Min. :19.22 Min. :21.50 Min. : 5.00
5 :19 1st Qu.:27.77 1st Qu.:21.50 1st Qu.:12.00
50 :18 Median :30.76 Median :22.00 Median :14.00
500:17 Mean :30.33 Mean :22.09 Mean :13.43
3rd Qu.:33.30 3rd Qu.:22.50 3rd Qu.:15.00
Max. :38.75 Max. :23.00 Max. :17.00
>
> summary(aov(weight ~ dose, data=litter))
Df Sum Sq Mean Sq F value Pr(>F)
dose 3 109.9 36.64 1.954 0.129
Residuals 70 1312.8 18.75
>
> round(cor(litter[,-1]),3)
weight gesttime number
weight 1.000 0.307 0.221
gesttime 0.307 1.000 -0.046
number 0.221 -0.046 1.000
>
> summary(aov(gesttime ~ dose, data=litter))
Df Sum Sq Mean Sq F value Pr(>F)
dose 3 1.135 0.3784 2.031 0.117
Residuals 70 13.044 0.1863
> summary(aov(number ~ dose, data=litter))
Df Sum Sq Mean Sq F value Pr(>F)
dose 3 43.3 14.45 2.315 0.0833 .
Residuals 70 436.8 6.24
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
共変量を調整してチューキーの方法で多重比較するには？
妊娠日数と仔ラットの数を調整しながら、仔ラット全体の体重を四用量群で多重比較。
ANOVAの関数aov()と多重比較の関数glht()を使う。
amod <- aov(weight ~ dose + gesttime + number, data = litter)
glht.res.t <- glht(amod, linfct = mcp(dose = "Tukey"))
summary(glht.res.t)
結果は、どの群間にも統計学的有意差なし。
> summary(glht.res.t)
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Tukey Contrasts
Fit: aov(formula = weight ~ dose + gesttime + number, data = litter)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
5 - 0 == 0 -3.3524 1.2908 -2.597 0.0546 .
50 - 0 == 0 -2.2909 1.3384 -1.712 0.3251
500 - 0 == 0 -2.6752 1.3343 -2.005 0.1958
50 - 5 == 0 1.0615 1.3973 0.760 0.8719
500 - 5 == 0 0.6772 1.3394 0.506 0.9574
500 - 50 == 0 -0.3844 1.4510 -0.265 0.9934
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- single-step method)
共変量を調整してダネットの方法で多重比較するには？
ダネットの方法はどうやるか？
dose=”Tukey”のところをdose=”Dunnett”に変える。
amod <- aov(weight ~ dose + gesttime + number, data = litter)
glht.res.d <- glht(amod, linfct = mcp(dose = "Dunnett"))
summary(glht.res.d)
ダネットの方法は、処置用量0群を対照として比較する。
今回は5と0の間が統計学的有意。
どう考えてデザインして、どう解析したいかによって、選ぶ方法が変わり、統計学的有意かどうかも変わってくる。
> summary(glht.res.d)
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Dunnett Contrasts
Fit: aov(formula = weight ~ dose + gesttime + number, data = litter)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
5 - 0 == 0 -3.352 1.291 -2.597 0.0316 *
50 - 0 == 0 -2.291 1.338 -1.712 0.2234
500 - 0 == 0 -2.675 1.334 -2.005 0.1255
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- single-step method)
共変量を調整してホックバーグの方法で多重比較するには？
ホックバーグ Hochbergの方法はBonferroni型のp値調整のひとつ。
あわせて読みたい
R でボンフェローニを実行する方法
検証試験において、三群以上の平均値を比較したいときに、単純に二群比較を繰り返すと有意水準が甘くなる。 有意水準の調整によって簡単に処理する方法がボンフェローニ…
Tukeyと同じ総当たりペアを解析して、p値調整法をHochbergにしたいと思う。
amod <- aov(weight ~ dose + gesttime + number, data = litter)
glht.res.t <- glht(amod, linfct = mcp(dose = "Tukey"))
summary(glht.res.t, test = adjusted("hochberg"))
どの群間も統計学的有意ではない。
控えめな結果だ。
> summary(glht.res.t, test = adjusted("hochberg"))
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Tukey Contrasts
Fit: aov(formula = weight ~ dose + gesttime + number, data = litter)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
5 - 0 == 0 -3.3524 1.2908 -2.597 0.0691 .
50 - 0 == 0 -2.2909 1.3384 -1.712 0.3661
500 - 0 == 0 -2.6752 1.3343 -2.005 0.2448
50 - 5 == 0 1.0615 1.3973 0.760 0.7919
500 - 5 == 0 0.6772 1.3394 0.506 0.7919
500 - 50 == 0 -0.3844 1.4510 -0.265 0.7919
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- hochberg method)
まとめ
統計ソフトRならば、共変量を調整しながら平均値の多重比較ができる。
aov()とglht()を使って、TukeyもDunnettもHochbergも実施できる。
参考になれば。
コメント