EZR で多重代入法を行う方法

EZR で多重代入法を行いたい場合、どのようにしたらよいか

EZR には、多重代入のメニューはないが、R スクリプト枠にスクリプトを書いていく方法で実行できる

はじめに

欠損値（欠測値と同じ）があるデータセットにおいて、推定値にバイアスがかかると言われており、欠損値を補完して解析をしたいという要望は多い

欠損値を補完する方法として、現在主流なのが、多重代入法である

EZR で行う方法を知りたい人は多い

しかし、2024 年 6 月 1 日現在、EZR のメニューで実行はできない

本記事では、EZR の R スクリプト窓に、R スクリプトを書くことで、EZR で多重代入法を行う方法を紹介する

EZR で多重代入法を行う準備

EZR で多重代入法を行うためには、まず準備が必要である

EZR を起動した後、以下の一行を R スクリプト窓に書く（もしくは、以下をコピペする）

install.packages("mice")

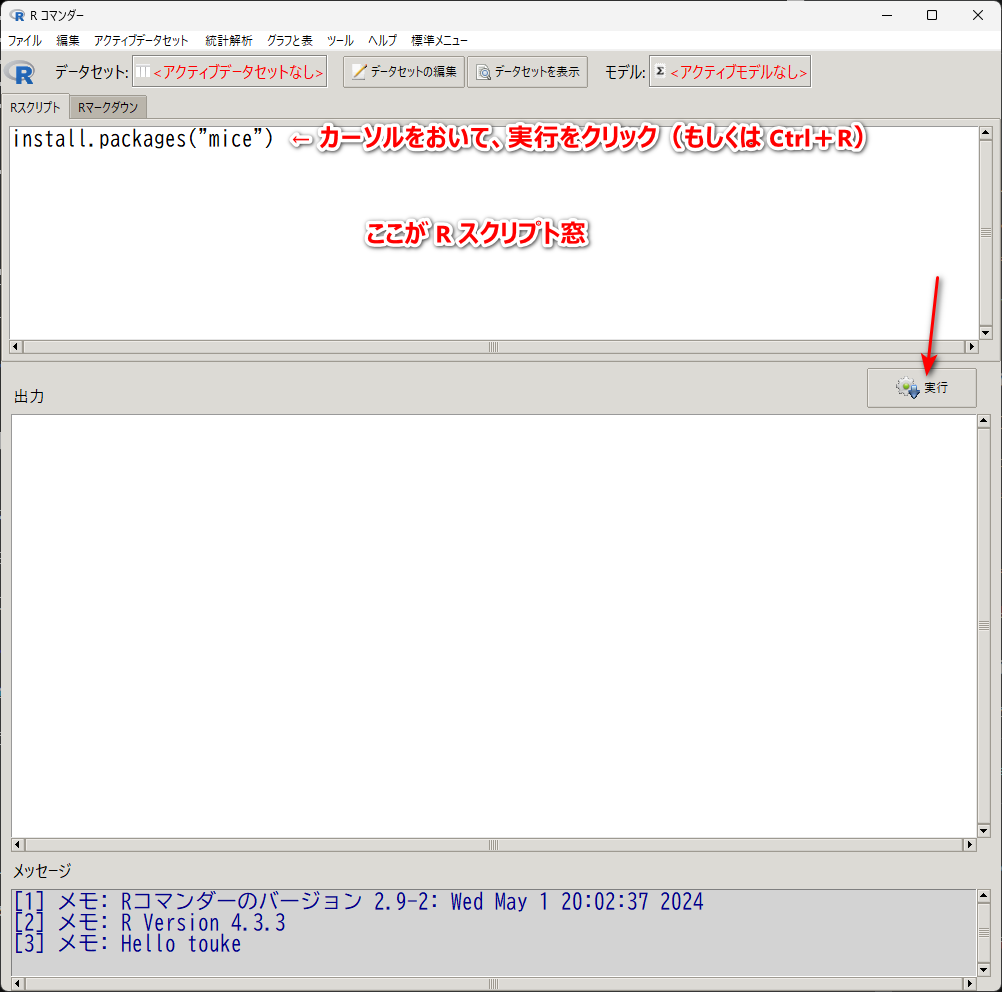
mice というのが、R の多重代入法のパッケージ名である

その mice パッケージのインストールを行わないといけない

これは、1 回だけでよい

この 1 行「install.packages(“mice”)」を書いた後、その行にカーソルをおいたままにして、実行ボタンをクリックする（あるいはキーボードの Ctrl と R を押す）と実行される

すると、以下のような窓が出現する

Japan (Yonezawa) を選択して、OK をクリックする

すると、mice パッケージが PC にインストールされる

これで、インストールが完了する

次に、以下の 1 行を書いて、実行する

library(mice)

これは、mice パッケージを呼び出す指令である

この library は、EZR を起動して mice を使いたいときは毎回、mice を使う前に、1 回だけ実行する

EZR が起動している間は、以後は実行する必要はない、そういう指令である

これで、多重代入法の準備が整った

多重代入で重回帰分析を行う方法

すべての変数が連続データの多変量線形回帰、いわゆる重回帰分析の場合、どのように R スクリプトを書くか紹介する

まず、エクセルなどから、欠損値を含むデータを EZR に取り込む

取り込んだデータセット名が Dataset であるとする

データ型の確認と変更方法

補完の前に、データセット内のデータの型が適切になっていると mice が自動で補完方法を選んでくれる

アクティブデータセット → 変数の操作 → データセット内の変数を一覧するを用いて、データ型を確認する

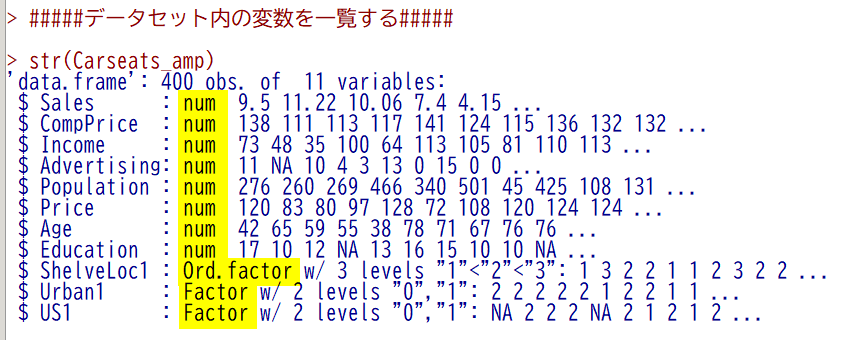
連続データは num、カテゴリカルデータ（順序なし）は Factor、カテゴリカルデータ（順序あり）は Ord.factor になっていれば、それに応じて適切な補完方法が選ばれる

適切なデータ型になっていない場合、アクティブデータセット → 変数の操作の中の

• 因子あるいは文字列として扱われている数値を連続変数に変換する

• 連続変数を因子に変換する

• 因子水準を再順序化する

を用いて、適切なデータ型に変更する

ただし、連続データに自動で適用される pmm（予測平均マッチング）は、カテゴリカルデータにも適用でき、全データに pmm を適用するのがよい

次節で設定方法を示す

補完方法

そこで、R スクリプト窓に以下の一行を書いて、実行する

imp <- mice(Dataset, m=100, maxit=10, method="pmm", seed=1)

ここで、imp は多重代入した後のデータセットの名前、m は多重代入データセット数、maxit は最大反復回数、method は補完方法（pmm は予測平均マッチングを示す）、seed は再現できるように、ランダム変数のシード（種）を指定したもの

データセット数は、m = 100 とした

100 から 1000 のデータセットが欲しいと言われている

多重代入データセットの数については、こちらも参照のこと

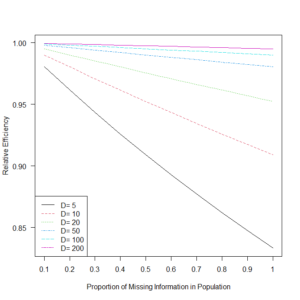
Fraction of Missing Information (FMI) という値の 100 倍を推奨している論文もある

Multiple imputation using chained equations: Issues and guidance for practice

maxit は、最大反復回数の意味だが、10 から 20 回は行うとされる

補完データセット一つにおける代入値を決める計算は、初期値を決めて、計算を繰り返すことで、収束させていくという方法を取るため、反復計算の回数を決める必要がある

ここでは、推奨の最低限の 10 とする（ただし、下記のスクショでは、デフォルトのまま（5 になっている）であるので、その点ご留意を）

method は前節で説明したとおり、連続データのほか、カテゴリカルデータにも適用できる方法で、最適な補完方法である

また、seed は、ここでは、1 としたが、何でもよい

通常は、正の整数にする（例：1, 12, 123, 1234 など）

出力窓に何やらたくさん出てくるが、多重補完されたことを示している変数名の一覧というだけなので、気にしない

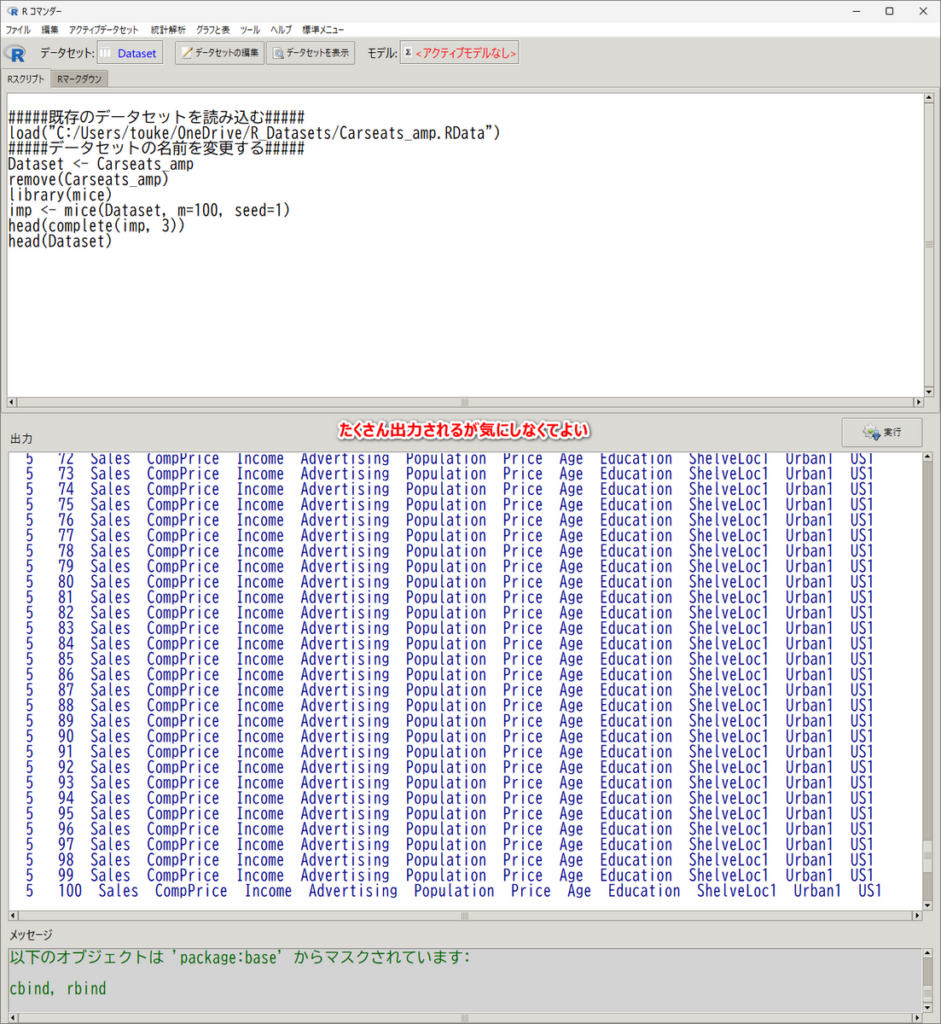
これで、多重補完した 100 のデータセットからなる多重代入データセット imp ができた

例えば、3 番目の補完データセットの先頭部分のみ少し見てみる場合、以下の一行を書くと見られる

head(complete(imp, 3))

ここで、head は先頭の 6 行を表示する指令、complete は、補完したデータを取り出す指令、 3 は、3 番目の補完データセットの指定という意味である

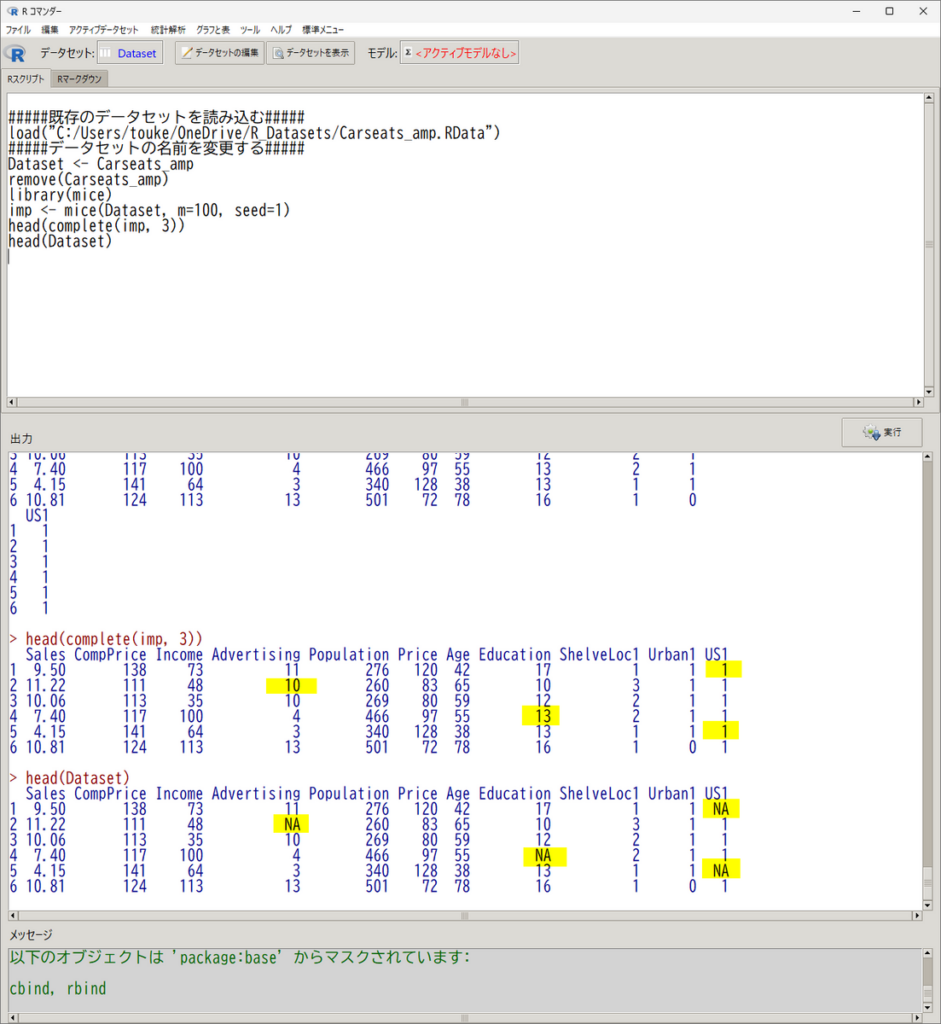
もともと、欠損値があった最初のデータセットと見比べてみると、確かに欠損値が補完されているのがわかる

3 番目ではなく、1 とか、 5 とかの数字にしてみると、ほかの数字で補完されていることがわかるので、見てみてほしい

では、欠損値が補完された 100 個のデータセットを使って、どうやって計算するか

計算方法

計算方法は、以下のように行う

2 行目の最後のカッコまで選択して、実行する

以下の、スクリプトを活用して、変数名を置き換えて活用してほしい

lm_imp <- with(imp, lm(Sales ~ Income + Population + Price + Age + Education))

ここで、

• lm_imp は、計算結果につける名前なので、何でもよい（ただし、半角英字先頭の半角英数のみがおすすめ。文字は _ と . が使える）
• with は 次に書いてある、ここでは imp という名前の多重補完したデータセットを使う関数
• lm は、単回帰、重回帰を行う関数
• Sales 以降は、回帰のモデル式で、~ の左側が目的変数、右側が説明変数で、+ でつなぐ（記号はすべて半角）

である

with と lm という関数名は変更せず、半角カッコや半角カンマの構造はそのままに、変数名は、ご自分の変数名に置き換えて、試してみてほしい

統合方法

計算結果は、100 個の補完データセットで計算された、100 個の結果が格納されている

これを統合して、結果を表示させるには、以下のように書いて実行する

summary(pool(lm_imp))

すると、以下の赤枠のように、統合された一つの計算結果が出てくる

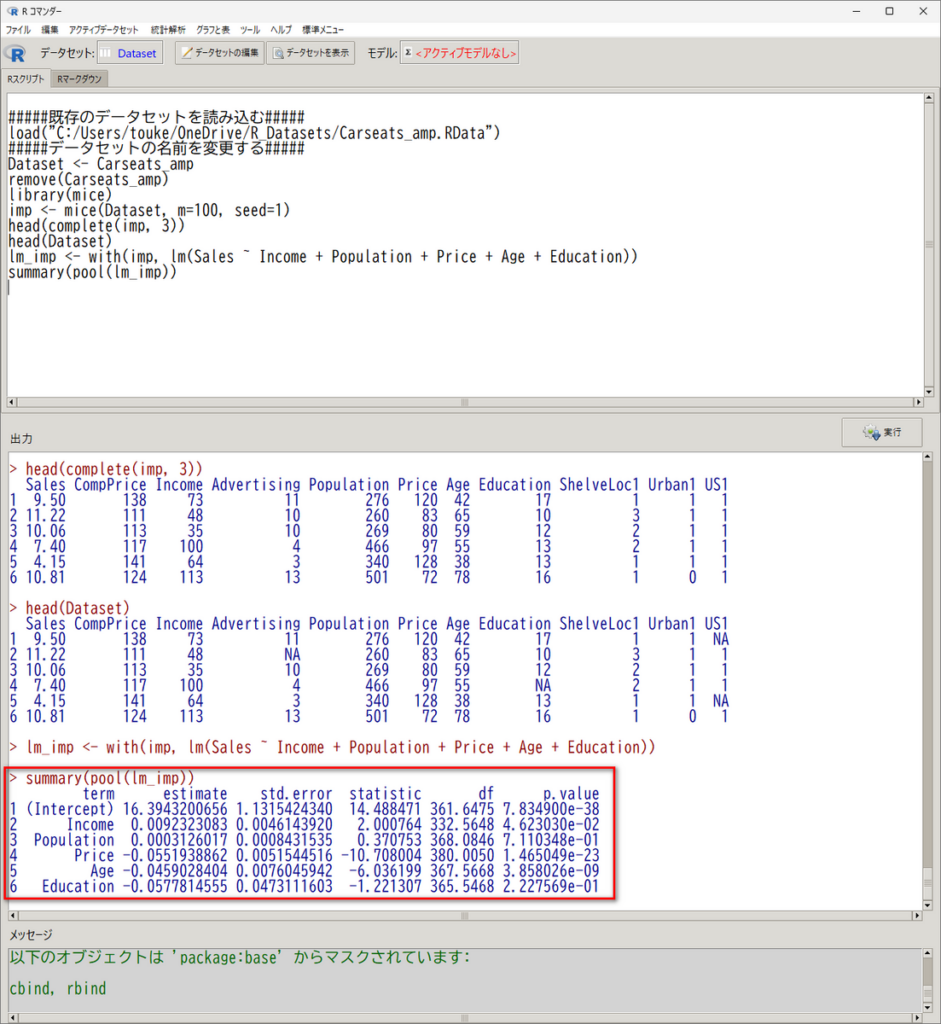
estimate （偏回帰係数）は、term（説明変数）が、1 上昇したときの、目的変数の推定値の変化を示している

右端の p.value が P 値で、これが、 0.05 未満であれば、estimate が 0 という帰無仮説が棄却されて、説明変数が 1 上昇したときの変化がゼロではなく統計学的に意味があると言えることになる

ちなみに、e-01, e-02 というのは、× 10 の －1乗 すなわち 0.1 倍、× 10 の － 2 乗 すなわち 0.01 倍という意味の科学的表現である

この例の場合、Age と Price と Income が 0.05 未満であり、統計学的有意である

Intercept（切片）は、ほかの説明変数が 0 のときの平均値で、この P 値には、出力されているが注目・解釈する必要はない

ちなみに、元のデータの結果と比べると、同様の結果であることが見て取れる

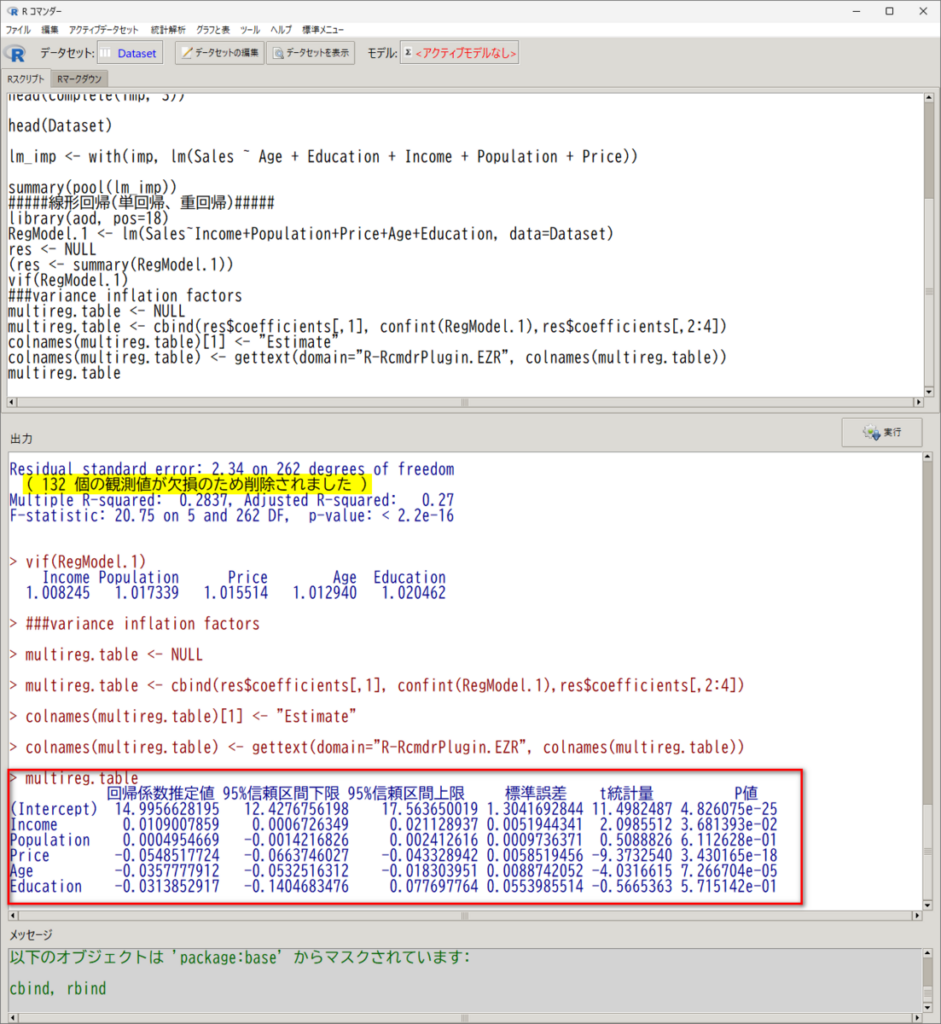
なので、今回の例では、欠損値がある元データの解析をメインにして、多重代入の結果をサブ（感度解析）というふうに示していくのがよいと思う

異なる場合は、多重代入することで、バイアスが取り除かれたと考えて進めるのもよいだろう

なお、95 ％信頼区間が必要な場合は、以下のように conf.int = 0.95 を加筆する

summary(pool(lm_imp), conf.int=0.95)

標準化偏回帰係数の計算方法

プールした後に標準化偏回帰係数を計算する関数はないため、プールする前に計算する必要がある

多重代入重回帰分析を行う前に、代入後に標準化しておくと、標準化偏回帰係数として求まる

それぞれの代入セットで計算された標準化偏回帰係数（標準化した目的変数と説明変数を使用して計算した偏回帰係数）をプールするという戦略をとると、統合標準化偏回帰係数が計算できる

標準化データ作成コードは以下のとおりである

install.packages("dplyr") # インストールは一回だけ
library(dplyr)

z_data <- complete(imp, action = "long", include = TRUE) %>%
  group_by(.imp) %>%  # 各代入セットごとにグループ化
  mutate(across(where(is.numeric), ~ scale(.) %>% as.vector)) %>% # すべての変数を標準化
  ungroup()

代入セットごとに、すべての変数を変数ごとに標準化する（scale という関数が標準化の関数）

いったんロング形式にしたデータセットを mids 形式に戻したあとは、型どおりの、解析、統合、結果出力の順番で進める

# 標準化済みデータをmiceオブジェクトに再変換
imp_z_data <- as.mids(z_data)

lm_imp_z <- with(imp_z_data, lm(Sales ~ Income + Population + Price + Age + Education))
summary(pool(lm_imp_z), conf.int=0.95)

結果は以下のとおりとなる

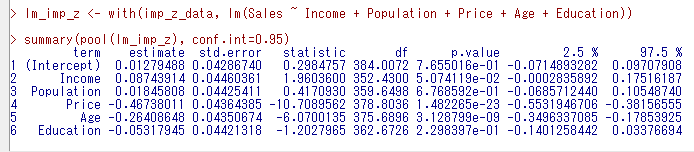
ここでは、estimate だけに着目する

この estimate が統合された標準化偏回帰係数である

絶対値が大きい説明変数が、相対的に影響力が大きい説明変数と言える

P 値は、標準化しない結果を使うようにし、ここで出力されている P 値は気にしない

カテゴリカルデータを説明変数に使っている場合

カテゴリカルデータが説明変数に入っている場合は要注意

二値の場合は、0 と 1 にしておくことで、問題ない

つまり、事前にダミー変数化しておくとよいという意味である

3 カテゴリ以上の場合は、いまのところ、よい解決策が思いつかない

最初から 0, 1 のダミー変数に変換しておけばよさそうだが、多重代入の際、複数のダミー変数の連携が難しい

複数のダミー変数で同じ症例において欠測が生じている状態になっているわけである

そのうちのどれか一つのダミー変数に 1 が代入されたら、ほかのダミー変数には 0 が代入される必要があるが、その制御が思いつかない

多重代入を行い共分散分析を行う場合

群の比較を背景因子で調整した多変量線形回帰、いわゆる共分散分析（カテゴリカルデータをダミー変数にした重回帰分析と同じ）の場合、どのように R スクリプトを書くか紹介する

補完方法までは、上記と同一である

計算方法と統合方法

計算方法は、以下の一行を R スクリプトに書く

変数名は、各自のデータセット内の変数名に変更してほしい

ancova_imp <- with(imp, lm(Sales ~ factor(US1) + Price + Age + Education))

Sales に関して、US1（二値のカテゴリカルデータ）の群間比較を、Price、Age、Education の共変量で調整した共分散分析という式である

統合方法も、上記と同様である

summary(pool(ancova_imp))

そうすると、以下のように計算結果が得られる

factor(US1)[T.1] というのは、US1 の 0 を参照カテゴリとして、1 の推定値が計算されていると読む（US1 が 0 と 1 のカテゴリカルデータの場合）

Price、Age、Education を調整しても、US とそれ以外で Sales の平均値の差は、統計学的有意と解釈できる

なお、95 % 信頼区間が必要であれば、conf.int = 0.95 を加筆する

summary(pool(ancova_imp), conf.int=0.95)

多重代入でロジスティック回帰分析を行う場合

ロジスティック回帰分析を行う場合は、glm 関数を使う

多重代入までは、上記と同じである

例えば、以下のように書いて、実行する

imp <- mice(Dataset, m=100, maxit=10, method="pmm", seed=1)

文字データのカテゴリカルデータは、数値（例えば、0, 1）に置き換えておくほうがスムーズと思う

解析は、例えば、以下のように書いて実行する

glm_imp <- with(imp, glm(event ~ exposure + age + sex, family=binomial))

~ の左側に目的変数、右側に説明変数を置く

family=binomial がロジスティック回帰を指定している

最後に、以下のように書いて実行すると、統合結果が得られる

pooled_glm <- pool(glm_imp)
summary(pooled_glm, exponentiate=TRUE, conf.int=0.95)

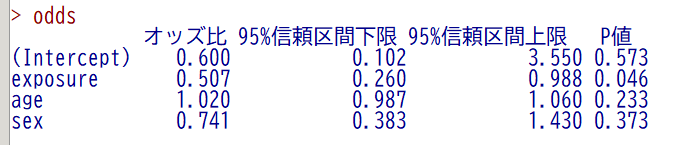
estimate が オッズ比で、2.5 %, 97.5 % が 95 % 信頼区間の下限と上限である

もともとの結果は以下のとおりで、方向性は同じだが、少々違うことがわかる

多重代入を行い Cox 回帰を行う場合

Cox 回帰（Cox の比例ハザードモデルと同じ）の場合も、補完データ作成は同じ

例えば、以下のように R スクリプト窓に書いて、実行する

imp <- mice(Dataset, m=100, maxit=10, method="pmm", seed=1)

次に、with と coxph を使って、解析を実行する

library(survival)
coxph_imp <- with(imp, coxph(Surv(time, status01) ~ age + sex + ph.ecog012 + meal.cal + wt.loss))

最後に、以下のように統合・結果出力を行う

pooled_cox <- pool(coxph_imp)
summary(pooled_cox, exponentiate=TRUE, conf.int=0.95)

オリジナルの欠測があるデータセットの場合は、以下のようになる

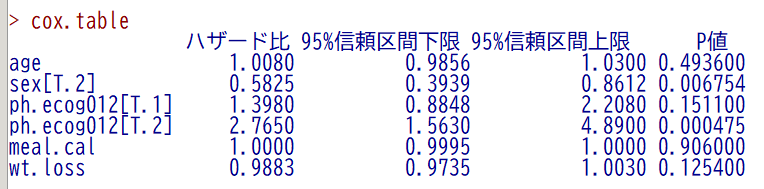
傾向は同じだが、少しだけ数値が異なるのがわかる

t 検定とカイ二乗検定はどうやるか

t 検定やカイ二乗検定と呼ばれている、2 群や 3 群以上の平均値や割合の単変量比較はどのようにすればよいか

といっても、t 検定、カイ二乗検定そのものを統合することはできない

平均値であれば、カテゴリカル変数一つのみを説明変数にした、回帰分析を行えば、t 検定統合の代用になる

割合であれば、カテゴリカル変数一つのみを説明変数にした、ロジスティック回帰分析を行えば、カイ二乗検定統合の代用になる

平均値の単変量解析

例えば、平均値の場合は、以下のようにする

mean_imp <- with(imp, lm(Sales ~ factor(US1)))
summary(pool(mean_imp), conf.int=0.95)

結果が出力されたら、カテゴリカル変数の P 値を確認する

1.389241e-03 となっている

ちなみに、これは、0.001389241 という数値の別の表記法である

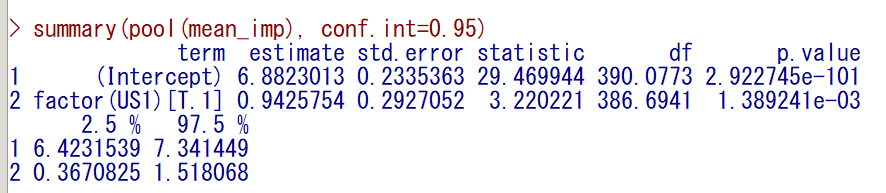
統合した平均値を出力したい場合は、以下のように少しだけスクリプトを変形する

lm のカッコ内の ~ （チルダ）の右側の最後に -1 が足されている

mean_imp1 <- with(imp, lm(Sales ~ factor(US1) -1))
summary(pool(mean_imp1, conf.int=0.95)

estimate の 6.882301 と 7.824877 がそれぞれ、US1=0 と US1=1 のときの統合平均値である

p.value は、統合平均値が 0 かどうかの検定なので、群間の有意差の P 値ではなく、気にしなくてよい

3 カテゴリでも参照カテゴリとの差が検討できる（この例の場合は、ShelveLoc = 1 が参照カテゴリ）

multcomp_imp <- with(imp, lm(Sales ~ factor(ShelveLoc1)))
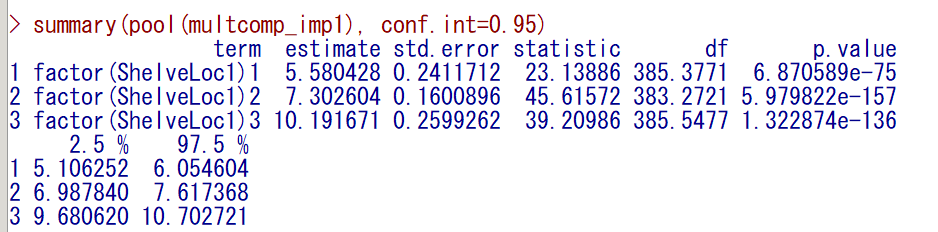
summary(pool(multcomp_imp), conf.int=0.95)

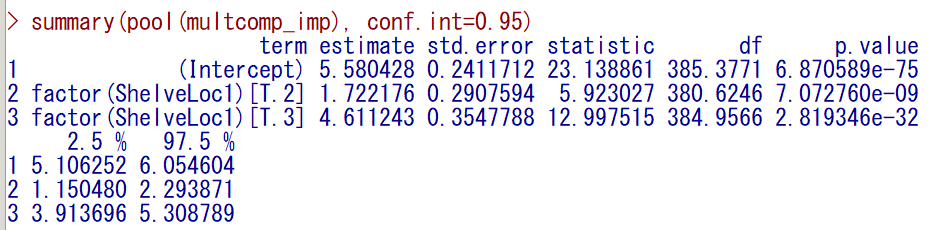
こちらも統合平均値を計算できる

multcomp_imp1 <- with(imp, lm(Sales ~ factor(ShelveLoc1) -1))
summary(pool(multcomp_imp1), conf.int=0.95)

estimate の列の 5.580428, 7.302604, 10.191671 がそれぞれの群の統合平均値である

割合の単変量解析

割合の場合は、以下のように書いて実行する

これは、exposure=0 と exposure=1 の各群の event の割合の比較を、exposure と event のオッズ比という指標を用いて行おうとする方法である

prop_imp <- with(imp, glm(event ~ exposure, family=binomial))
summary(pool(prop_imp), exponentiate=TRUE, conf.int=0.95)

exposure の行の 0.04473540 が統合 P 値である

exposure = 0 と exposure = 1 に有意差ありということになる

exposure = 0 と exposure = 1 のそれぞれの割合をロジスティックモデルの推定値は計算された数値を使って直接計算すると、求めることができる

まず、exponentiate しない結果を出力する

Intercept の estimate （ロジット）を割合に変換したものが、exposure = 0 の割合の統合推定値（約 0.599）である

Intercept と exposure[T.1] の estimate を足し合わせた（今回の場合は exposure = 1 の estimate が負の値なので引き算になっている）ロジットを割合に変換したものが、exposure = 1 の割合の統合推定値（約 0.445）である

これらの割合は、欠測値がある元のデータセットでクロス集計したときの割合と大きくは異ならないことが確認できる（exposure = 0 は、61.0 ％、exposure = 1 は、44.9 %）

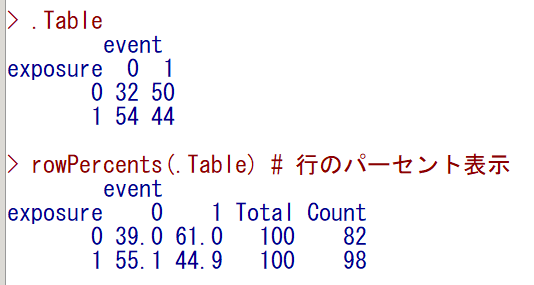
ここでは、2 群で示したが、3 群以上でも同様に解析できると思う

emmeans を使って統合平均や統合割合を計算する方法

emmeans パッケージの emmeans 関数を使うと、統合平均値や統合割合を求めることができる

統合 P 値も求められる

上記の例とは異なるが、まず、t 検定代わりの単変量回帰分析を以下に示す

imp.lm1 <- with(imp, lm(A ~ Treat))
summary(pool(imp.lm1), conf.int=TRUE)
library(emmeans)
emmeans(imp.lm1, specs="Treat")
pairs(emmeans(imp.lm1, specs="Treat"))

多重代入データセット imp を作成するところまでは、一緒である

lm を使って t 検定の代わりにするところも同様である

今回は、A という連続データを Treat あり、なしで比較する t 検定とする

結果出力は以下のようになる

> summary(pool(imp.lm1), conf.int=TRUE)
         term  estimate std.error  statistic       df      p.value     2.5 %    97.5 %
1 (Intercept) 52.748780  1.574748 33.4966539 116.0380 1.729354e-61 49.629805 55.867756
2      Treat1 -1.383945  1.952216 -0.7089098 114.6822 4.798191e-01 -5.251023  2.483133

> library(emmeans)
> emmeans(imp.lm1, specs="Treat")
 Treat emmean   SE  df lower.CL upper.CL
 0       52.7 1.57 116     49.6     55.9
 1       51.4 1.15 112     49.1     53.7

Confidence level used: 0.95 

> pairs(emmeans(imp.lm1, specs="Treat"))
 contrast        estimate   SE  df t.ratio p.value
 Treat0 - Treat1     1.38 1.95 115   0.709  0.4798

emmeans で 統合平均値と95% 信頼区間、pairs で 統合 P 値が得られる

これで、上記の -1 を使う方法と同じ結果が得られる

> imp.lm1_1 <- with(imp, lm(A ~ Treat -1))
> summary(pool(imp.lm1_1), conf.int=TRUE)
    term estimate std.error statistic       df      p.value    2.5 %   97.5 %
1 Treat0 52.74878  1.574748  33.49665 116.0380 1.729354e-61 49.62980 55.86776
2 Treat1 51.36484  1.153827  44.51693 112.0459 4.493632e-73 49.07869 53.65099

次に、統合割合のために、単変量ロジスティック回帰を行う

imp.lm3 <- with(imp, glm(Sex ~ Treat, family=binomial))
summary(pool(imp.lm3), conf.int=TRUE)
emmeans(imp.lm3, specs="Treat")

単変量ロジスティックは行うが、オッズ比を求めることが目的ではないので、exponentiate はしない

emmeans での結果は、対数オッズ比（ロジット）であるので、Intercept の estimate と、Treat = 0 の emmean が同一であることがわかる（約 0.147）

> imp.lm3 <- with(imp, glm(Sex ~ Treat, family=binomial))
> summary(pool(imp.lm3), conf.int=TRUE)
         term   estimate std.error  statistic      df   p.value      2.5 %    97.5 %
1 (Intercept)  0.1466035 0.3131866  0.4681027 116.038 0.6405892 -0.4736999 0.7669068
2      Treat1 -0.3242847 0.3861594 -0.8397689 116.038 0.4027649 -1.0891194 0.4405501

> emmeans(imp.lm3, specs="Treat")
 Treat emmean    SE  df asymp.LCL asymp.UCL
 0      0.147 0.313 Inf    -0.467     0.760
 1     -0.178 0.226 Inf    -0.620     0.265

Results are given on the logit (not the response) scale. 
Confidence level used: 0.95 

emmeans の結果は、上記でも同様に計算したとおり、Intercept と Treat1 の estimate を足した数が、Treat=1 の emmean になっている (-0.178)

この結果から、データを取り出して、plogis という関数を適用すると、対数オッズ比が割合に変換される

# summary()でデータフレーム形式に変換
emmeans_summary <- summary(imp.emmeans3)

# emmean（推定値）を plogis で変換
emmeans_summary$prob <- plogis(emmeans_summary$emmean)

# 信頼区間も変換
emmeans_summary$prob_LCL <- plogis(emmeans_summary$asymp.LCL)
emmeans_summary$prob_UCL <- plogis(emmeans_summary$asymp.UCL)

# 結果を確認
print(emmeans_summary)

結果は、以下のとおりで、出力の右半分の prob, prob_LCL, prob_UCL が割合と95% 信頼区間下限・上限である

> # 結果を確認
> print(emmeans_summary)
 Treat emmean    SE  df asymp.LCL asymp.UCL  prob prob_LCL prob_UCL
 0      0.147 0.313 Inf    -0.467     0.760 0.537    0.385    0.681
 1     -0.178 0.226 Inf    -0.620     0.265 0.456    0.350    0.566

Results are given on the logit (not the response) scale. 
Confidence level used: 0.95 

検定は、pairs で計算できる

pairs(emmeans(imp.lm3, specs="Treat"))

結果は、以下のとおりで、summary(pool)) で出力した P 値とほぼ同様である

> pairs(emmeans(imp.lm3, specs="Treat"))
 contrast        estimate    SE  df z.ratio p.value
 Treat0 - Treat1    0.324 0.386 Inf   0.840  0.4010

Results are given on the log odds ratio (not the response) scale. 

補完値はどうやって生成しているのか

連続データでも、カテゴリカルデータでも、予測平均マッチング（predictive mean matching, PMM）という方法を使うという話をしてきた

PMM は、線形回帰（重回帰）モデルによる代入方法を基礎にしている

線形回帰モデルによる代入方法は、欠損値を除いた完全データで、欠損値を含む連続データを予測する重回帰式を基にして、補完する方法である

PMM は、その線形回帰モデルで計算される「欠測データの予測値候補」と、実際に観測されている「観測データの完全データからの予測値」の差（距離）が近い K 人を選び、その中からランダムに選んだ人の観測データを補完値とする方法である

K は、5 から 10 とか、3 から 10 とか、が良いと言われており、mice は、5 に設定されていて、変更は不要である

詳細は、野間 2017 参照

以下も、よければ参照

Tuning multiple imputation by predictive mean matching and local residual draws

まとめ

多重代入法を EZR で実施する方法を解説した

多重代入法は、欠損値の多重代入・解析・統合の 3 ステップが一つになった方法である

mice パッケージの mice と pool を使って実施する

重回帰、共分散分析（群間の背景を調整することが目的の重回帰）、ロジスティック回帰、Cox 回帰の方法について解説した

カテゴリカルデータを説明変数にした単回帰、ロジスティック回帰を使えば、t 検定やカイ二乗検定の統合の代わりになることも説明した

何らか参考になれば幸い

参考文献

連鎖方程式による多重代入法

mice: Multivariate Imputation by Chained Equations in R | Journal of Statistical Software

Tuning multiple imputation by predictive mean matching and local residual draws

Multiple imputation using chained equations: Issues and guidance for practice