説明変数がいくつかある生存時間データで、いくつかの説明変数に欠損値があり、多重代入して IPTW Cox 回帰分析がしたい場合、R でどのようにすればよいか
IPTW Cox 回帰の場合、ブートストラップ信頼区間がより適切であるが、それはどうやるか
多重代入とは
データセットに、欠損値があり、欠損値処理として多重代入を採用したいときがある
多重代入とは、いくつか適切と思われる数値で、欠損値を補完して、ひとつではなく、いくつかのデータセットを作成する
いくつかのデータセットから計算した結果を統合するという方法である
こちらの記事も参照のこと

IPTW 法とは
比較する群間の交絡因子の調整方法の一つで、傾向スコアの逆数を重みとして、人数をかさましして計算する方法
これによって、測定できている交絡因子に限っては、あたかも群間でそろっている、つまりは、交絡していないような状態を作り出すことができる
ただし、測定できている変数のみであって、未知・未測定の交絡因子は調整できていないため、ランダム化比較試験と同等にはならないことに注意する必要がある
こちらの記事も参照のこと

IPTW Cox 回帰とは
IPTW で重み付けした、Cox 回帰分析のこと
Cox 回帰は、Cox 比例ハザードモデルを用いた回帰分析のこと
こちらの記事も参照のこと

ブートストラップ信頼区間とは
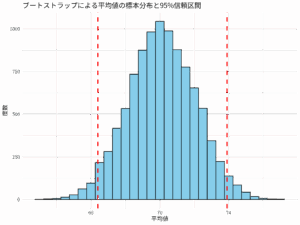
ブートストラップ信頼区間は、今回得られているサンプルを活用して、復元抽出(抽出しては戻すを繰り返すので、同じデータが抽出されることもある)を繰り返し、サンプルと同じ大きさの疑似サンプルを多数作成して、そのデータセット群を分析することで、点推定値の分布から計算された信頼区間のことである
こちらの記事も参照のこと

多重代入 IPTW Cox 回帰 ブートストラップ信頼区間の計算方法
以下に、スクリプトを示す
全体の流れは、以下のようになっている
- 欠損値を含むデータセットを準備する
- mice パッケージの mice 関数で多重代入データを作成する
- MatchThem パッケージの weightthem 関数で IPTW を作成する
- いったん、多重代入データセットを使った暫定的な IPTW Cox 回帰を行う(IPTW に対応したロバスト信頼区間というものが計算される)
- ブートストラップ信頼区間計算のために、ブートストラップデータセットを用いた Cox 回帰の関数を定義する(cox_reg)
- 多重代入データセットのオブジェクト名を準備する(imp1 ~ imp5)
- 多重代入データセット一つ一つに対して、boot パッケージの boot 関数によってブートストラップ法を実行する
- ブートストラップ結果を格納するリストを作成する
- ブートストラップ結果を取り出す
- 推定値と標準誤差を元に統合推定値と統合信頼区間の計算
- ブートストラップ信頼区間を出力
- ロバスト信頼区間とブートストラップ信頼区間を並べて比較
# 欠損値を含むデータセットを準備する
# ph.ecog01, meal.cal, wt.loss:欠損値含む
df0 <- df[,c("time", "status01", "ph.ecog01", "age", "sex",
"meal.cal", "wt.loss")]
# mice パッケージの mice 関数で多重代入データを作成する
# (データセット数 m=5):本当は少なくとも m=100 がよい
library(mice)
df_imputed <- mice(df0, seed=0)
df_imputed
# MatchThem パッケージの weightthem 関数で IPTW を作成する
library(MatchThem)
weighted_imputed <- weightthem(ph.ecog01 ~ age + factor(sex) +
meal.cal + wt.loss, data=df_imputed)
summary(weighted_imputed)
# 多重代入データセットを使った暫定的な IPTW Cox 回帰を行う
#(ロバスト信頼区間)
library(survival)
wi_iptw_cox <- with(weighted_imputed,
coxph(Surv(time, status01) ~
ph.ecog01 + age + factor(sex) +
meal.cal + wt.loss,
weights=weights,
robust=TRUE
))
## 統合
pooled_wi_iptw_cox <- pool(wi_iptw_cox)
summary(pooled_wi_iptw_cox, conf.int=TRUE, exponentiate = TRUE)
# ブートストラップ信頼区間計算のために、
# ブートストラップデータセットを用いた Cox 回帰の関数を定義する
# cox_reg 関数: 特定の完全データセットに対して
# Cox比例ハザードモデルを適用し、回帰係数を返す関数
cox_reg <- function(data, indices)
# ブートストラップ標本の抽出
data <- data[indices,]
# Cox比例ハザードモデルの適用
fit <- with(data,
coxph(Surv(time, status01) ~
ph.ecog01 + age + factor(sex) +
meal.cal + wt.loss, weights=weights,
robust=TRUE
))
# ハザード比の推定値を返す
return(coef(fit))
}
# 多重代入データセットのオブジェクト名を準備する
# imps ベクトル: ブートストラップの各試行で使用する
# 完全データセットの識別子(m=1~5 まで)
imps <- paste0("imp", 1:weighted_imputed$object$m)
# 多重代入データセット一つ一つに対して、
# boot パッケージの boot 関数によってブートストラップ法を実行する
library(boot)
for (imp_name in imps){
# 完全データセットの作成
imp <- complete(weighted_imputed,
action = as.numeric(substr(imp_name, 4, 6)))
result <- cox_reg(data=imp, indices=1:nrow(df0))
set.seed(0)
boot_res <- boot(
data = imp,
statistic = cox_reg,
# サンプリング回数:10000 のほうがよいが取り急ぎ 1000
R = 1000
)
print(boot_res)
# ブートストラップ結果を保存
assign(paste("boot_res_", imp_name, sep=""), boot_res)
}
# ブートストラップの結果を格納するリストを作成する
boot_res_lists <- lapply(paste0("boot_res_imp",
1:weighted_imputed$object$m), get)
# ブートストラップ結果を取り出す
## 推定値と標準誤差のベクトルを初期化
estimates <- c()
variances <- c()
## forループで各ブートストラップの結果を処理
for (i in 1:5) {
m <- mean(boot_res_lists[[i]]$t[, 1])
se <- sd(boot_res_lists[[i]]$t[, 1])
estimates <- c(estimates, m)
variances <- c(variances, se^2)
}
# 推定値と標準誤差を元に統合推定値と信頼区間の計算
pool <- pool.scalar(Q = estimates, U = variances, n = nrow(df0))
## プール標準誤差を計算
## t1* (ph.ecog01) の SE の統合
pooled_se <- sqrt(pool$ubar)
## 統合推定値の取り出し
pooled_m <- pool$qbar
## 95 %信頼区間の計算
LL <- pooled_m - qnorm(0.975)*pooled_se
UL <- pooled_m + qnorm(0.975)*pooled_se
# ブートストラップ信頼区間を出力
output <- c(pooled_m, LL, UL)
names(output) <- c("Estimate", "LowerLimit", "UpperLimit")
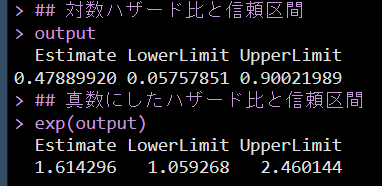
## 対数ハザード比と信頼区間
output
## 真数にしたハザード比と信頼区間
exp(output)
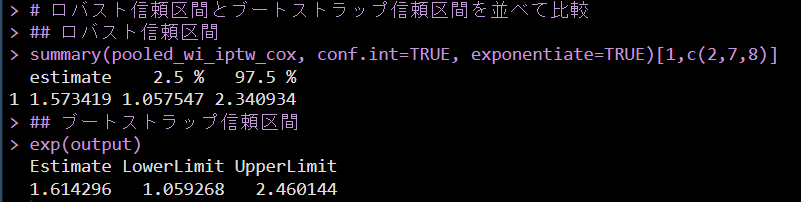
# ロバスト信頼区間とブートストラップ信頼区間を並べて比較
## ロバスト信頼区間
summary(pooled_wi_iptw_cox, conf.int=TRUE,
exponentiate=TRUE)[1,c(2,7,8)]
## ブートストラップ信頼区間
exp(output)結果は、以下のように出力される
暫定的な結果(ロバスト信頼区間)は以下のとおり

ここでは、着目している ph.ecog01 の交絡因子の推定値も表示されている
IPTW を作成するために使用した交絡因子を、再度共変量として投入している
ブートストラップ信頼区間の出力は以下のとおり
ロバスト信頼区間とブートストラップ信頼区間を並べてみると、少し異なるのがわかる
まとめ
この記事では、多重代入 IPTW Cox 回帰 ブートストラップ信頼区間 の一連の計算を R ではどのようなスクリプトを書けば実現できるかの例を挙げた
一つで完結する関数はないので、いくつかの関数を組み合わせて、実行する必要がある
何らか参考になれば




コメント