SPSS で重回帰分析をしたい場合、どのようにすればよいか
やりたいこと別にまとめてみた
説明変数が連続データの場合で、交絡因子調整が目的の場合
目的変数、説明変数ともに連続データで、交絡因子調整が目的の場合は、以下のように解析する
分析 → 回帰 → 線型 を選択
目的変数、説明変数（着目している変数、交絡因子）を投入したら、OK をクリック
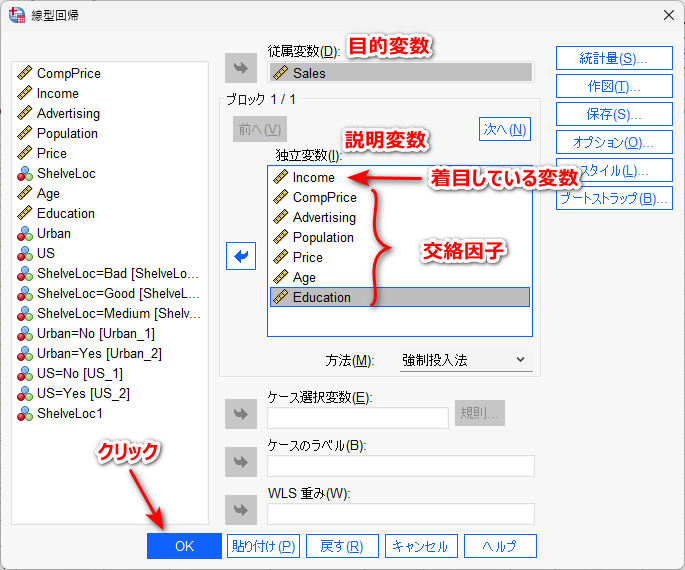
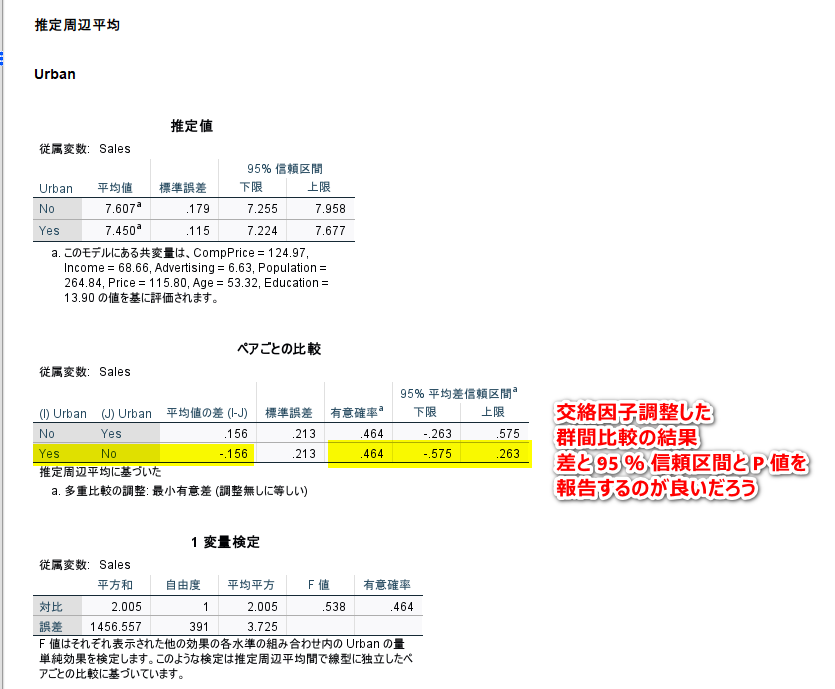
結果は、以下のように確認し、必要な数値を表にまとめて、解釈を加える
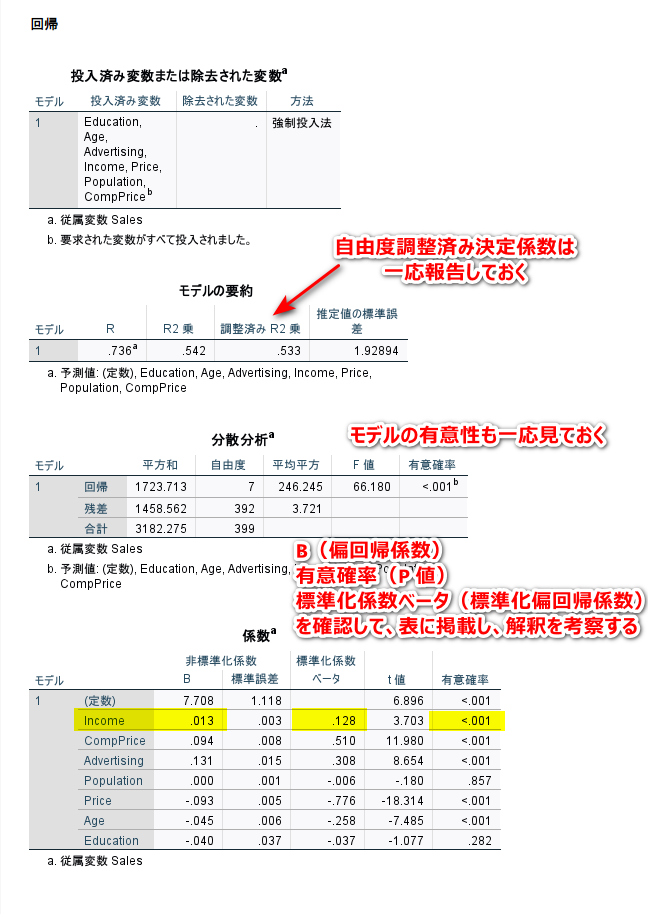
重回帰分析で、どんな数値を報告すべきかは、こちらを参照
説明変数がカテゴリカルデータ（群間比較）の場合で、交絡因子調整が目的の場合
目的変数が連続データ、説明変数がカテゴリカルデータで群間比較を行いたくて、交絡因子調整を目的としている場合は、以下のように解析する
分析 → 一般線型モデル → 1 変量 を選択
目的変数、説明変数（因子）、説明変数（共変量）を投入したら、EM 平均をクリック
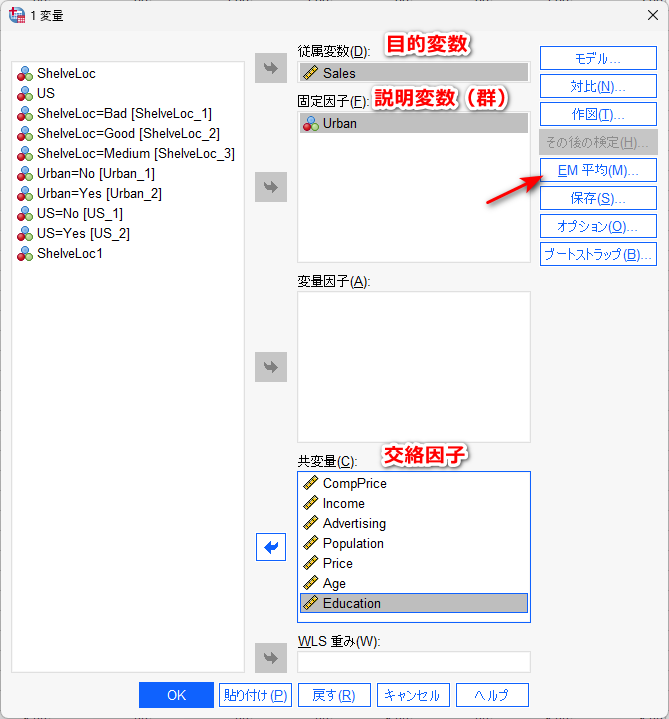
群を投入して、主効果の比較にチェック
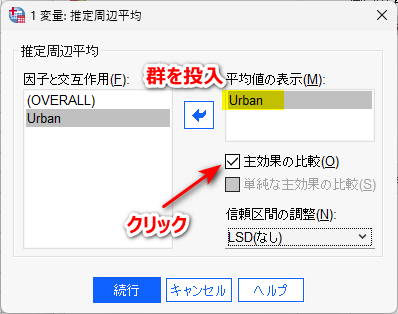
続行で戻り、OK をクリックすると解析される
関連のある因子を統計解析的に探索的に検討してみたい
分析 → 回帰 → 線型を用いる
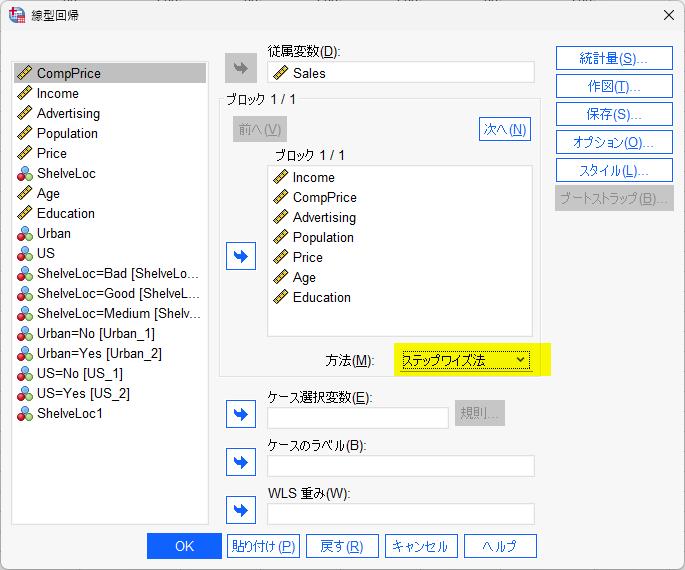
目的変数を投入し、関連を検討したい因子を説明変数として投入したら、方法をステップワイズ法とする
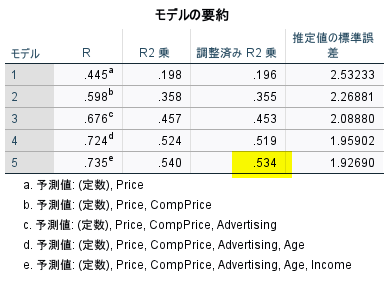
自由度調整済み決定係数が一番大きい数値になったモデルが、計算上もっともよい説明変数セットという意味になる
今回の場合は、全ての説明変数を投入したときがもっともよいセットということになった
この結果は、今回のデータではもっともよい結果であるが、再度サンプリングしたデータでは同じにはならない
なので、この計算上の結果をうのみにして報告するのではなく、あくまで探索的な検討の一環として考えるべきである
関連する因子、交絡因子のセットは、先行研究の知見と理論・理屈が重要であり、統計解析結果は、それを補うものと考えるのがよい
階層的なモデルを作成して、モデルの当てはまりが変化するのを見てみたい
説明変数が、いくつかのグループに分けられる場合、そのグループごとに、階層的に投入することで、自由度調整済み決定係数が変化し、あてはまりが変わっていくさまを観察したい場合
ブロックという機能を使う
例えば、今回の例題の場合、人口学的要因（Age, Education, Income, Population）、外的要因（CompPrice, Advertising, Price）というふうにわけられると考えるとすると、以下のように階層的に投入することが可能である
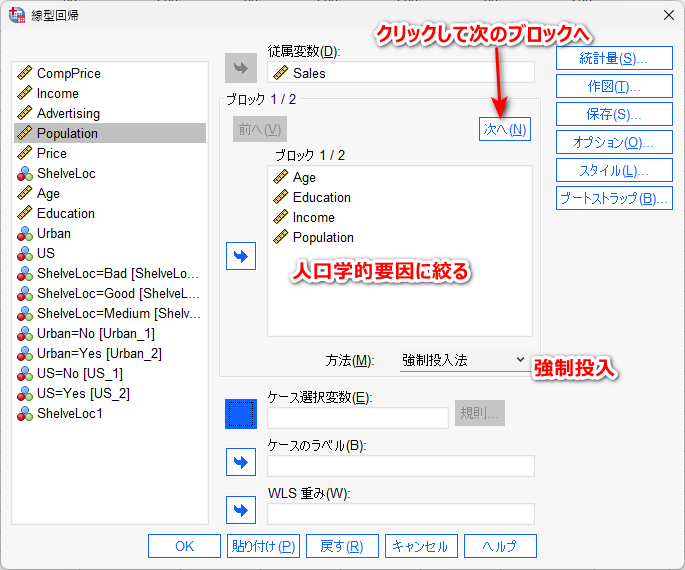
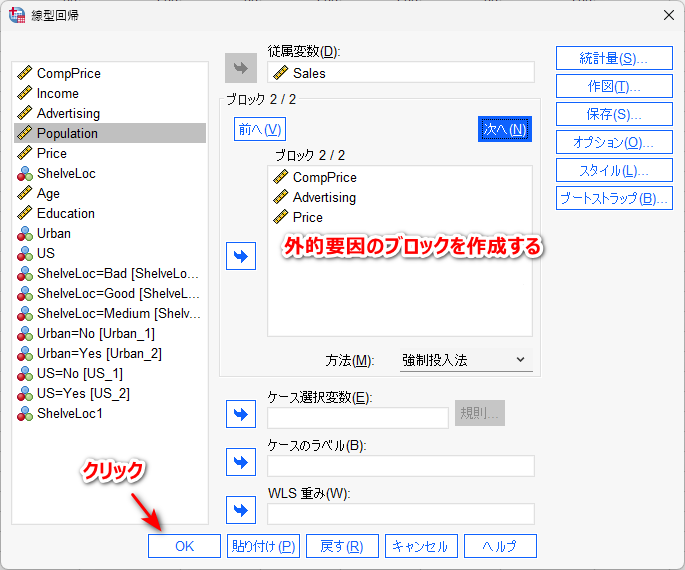
結果は以下のとおりで、外的要因の 3 つの変数を投入すると、自由度調整済み決定係数が顕著に増加し、外的要因変数が目的変数に大きく関連していることが示唆される
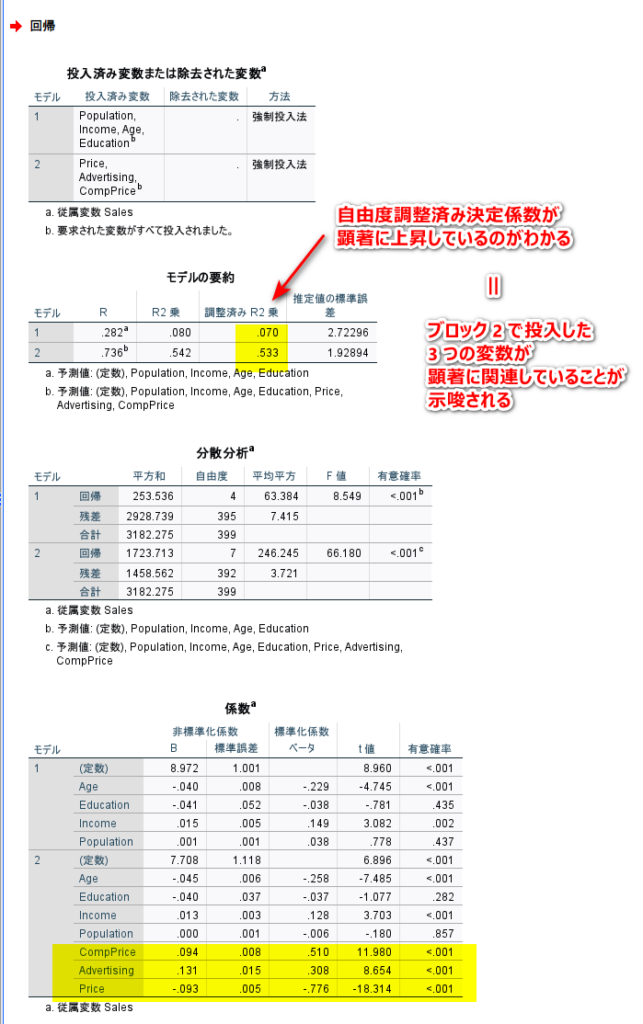
まとめ
重回帰分析を SPSS で行う方法を解説した
やりたいこと別にまとめて、交通整理した
何らか参考になれば幸い
おすすめ書籍
SPSSで学ぶ医療系データ解析 第2版
SPSSで学ぶ医療系多変量データ解析 第2版
コメント