R で重回帰分析を行う具体例 ― ISLR パッケージ Auto データセットを使った重回帰分析

R の ISLR パッケージの Auto データセットを使った分析例。

データの準備

最初の一回だけ、ISLRパッケージをインストール。

install.packages("ISLR")

ISLRパッケージを呼び出して、解析開始。

library(ISLR)

ISLRパッケージのAutoデータセットを用いて解析。

9変数、392例のデータ。

> str(Auto)
'data.frame':   392 obs. of  9 variables:
$ mpg         : num  18 15 18 16 17 15 14 14 14 15 ...
$ cylinders   : num  8 8 8 8 8 8 8 8 8 8 ...
$ displacement: num  307 350 318 304 302 429 454 440 455 390 ...
$ horsepower  : num  130 165 150 150 140 198 220 215 225 190 ...
$ weight      : num  3504 3693 3436 3433 3449 ...
$ acceleration: num  12 11.5 11 12 10.5 10 9 8.5 10 8.5 ...
$ year        : num  70 70 70 70 70 70 70 70 70 70 ...
$ origin      : num  1 1 1 1 1 1 1 1 1 1 ...
$ name        : Factor w/ 304 levels "amc ambassador brougham",..: 49 36 231 14 161 141 54 223 241 2 ...
>

name以外の変数を使う。

Auto1 <- Auto[1:8]

Miles per gallonを予測する因子の相関係数

origin以外の7つの変数で相関係数行列を作成する。

> round(cor(Auto1[1:7]),3)
mpg cylinders displacement horsepower weight acceleration   year
mpg           1.000    -0.778       -0.805     -0.778 -0.832        0.423  0.581
cylinders    -0.778     1.000        0.951      0.843  0.898       -0.505 -0.346
displacement -0.805     0.951        1.000      0.897  0.933       -0.544 -0.370
horsepower   -0.778     0.843        0.897      1.000  0.865       -0.689 -0.416
weight       -0.832     0.898        0.933      0.865  1.000       -0.417 -0.309
acceleration  0.423    -0.505       -0.544     -0.689 -0.417        1.000  0.290
year          0.581    -0.346       -0.370     -0.416 -0.309        0.290  1.000

Miles per gallonを国別に比較

origin別のmpg(miles per gallon=燃費)をANOVAで分析する。

originの内容は以下の通り。

Origin of car (1. American, 2. European, 3. Japanese)

res.origin <- lm(mpg ~ factor(origin), data=Auto1)
summary(res.origin)

アメ車に比べヨーロッパ車は燃費がいいし、日本車はさらにいい。

Estimateがmiles per gallon推定値で、アメ車に＋7.6がヨーロッパ車、＋10.4が日本車。

> summary(res.origin)
Call:
lm(formula = mpg ~ factor(origin), data = Auto1)
Residuals:
Min      1Q  Median      3Q     Max
-12.451  -5.034  -1.034   3.649  18.966
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)      20.0335     0.4086  49.025   <2e-16 ***
factor(origin)2   7.5695     0.8767   8.634   <2e-16 ***
factor(origin)3  10.4172     0.8276  12.588   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.396 on 389 degrees of freedom
Multiple R-squared:  0.3318,    Adjusted R-squared:  0.3284
F-statistic:  96.6 on 2 and 389 DF,  p-value: < 2.2e-16

Miles per gallonを予測する重回帰モデルの作成

全部の変数でmpgを推測するモデルを作成してみる。

res1 <- lm(mpg ~ cylinders + displacement + horsepower + weight + acceleration + year + factor(origin), data=Auto1)
summary(res1)

Adjusted R-squaredが0.8205と高く、この重回帰モデルの説明変数は目的変数をよく説明している。

displacement (排気量), weight, year, originは統計学的有意に関連あり。

例えば、yearが1増加する（1年新しくなる）と、mpgが0.777増加（燃費向上）する。

> summary(res1)
Call:
lm(formula = mpg ~ cylinders + displacement + horsepower + weight +
acceleration + year + factor(origin), data = Auto1)
Residuals:
Min      1Q  Median      3Q     Max
-9.0095 -2.0785 -0.0982  1.9856 13.3608
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)     -1.795e+01  4.677e+00  -3.839 0.000145 ***
cylinders       -4.897e-01  3.212e-01  -1.524 0.128215
displacement     2.398e-02  7.653e-03   3.133 0.001863 **
horsepower      -1.818e-02  1.371e-02  -1.326 0.185488
weight          -6.710e-03  6.551e-04 -10.243  < 2e-16 ***
acceleration     7.910e-02  9.822e-02   0.805 0.421101
year             7.770e-01  5.178e-02  15.005  < 2e-16 ***
factor(origin)2  2.630e+00  5.664e-01   4.643 4.72e-06 ***
factor(origin)3  2.853e+00  5.527e-01   5.162 3.93e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.307 on 383 degrees of freedom
Multiple R-squared:  0.8242,    Adjusted R-squared:  0.8205
F-statistic: 224.5 on 8 and 383 DF,  p-value: < 2.2e-16

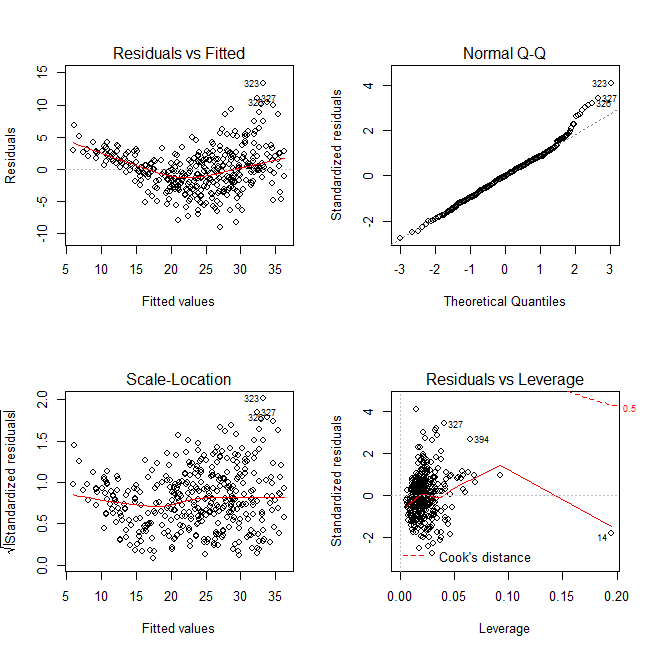
残差プロット。

予測式の性能チェック。

Residuals vs. FittedとScale-Locationは水平な赤い線が理想。

Normal Q-Qはすべての点が斜めの線上であるのが理想。

Residuals vs. Leverageは赤い点線より外側に点がないのが理想。

Residual vs. Fittedは、厳密にいうと、heteroscedasticity（分散不均一性）に見える。

Normal Q-Qは、Quartileが大きいところでずれがある。

Scale-LocationとResiduals vs. Leverageは取り立てて問題点はない。

layout(t(matrix(c(1:4),nr=2)))
plot(res1)

交互作用項を入れた解析

例として、yearとdisplacementの交互作用項を追加して再度解析。

res2 <- lm(mpg ~ cylinders + displacement + horsepower + weight + acceleration + year + year:displacement + factor(origin), data=Auto1)
summary(res2)

displacementとyearの交互作用項を足してみたところ、

displacement:year: p=3.51e-12 ***

という結果を得た。

この項は統計学的有意であった。

> summary(res2)
Call:
lm(formula = mpg ~ cylinders + displacement + horsepower + weight +
acceleration + year + year:displacement + factor(origin),
data = Auto1)
Residuals:
Min      1Q  Median      3Q     Max
-7.5860 -2.0066  0.0133  1.6529 12.1025
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)       -6.451e+01  7.829e+00  -8.241 2.77e-15 ***
cylinders          2.606e-02  3.103e-01   0.084   0.9331
displacement       2.806e-01  3.642e-02   7.704 1.15e-13 ***
horsepower        -3.370e-02  1.306e-02  -2.580   0.0103 *
weight            -6.116e-03  6.212e-04  -9.844  < 2e-16 ***
acceleration       1.048e-01  9.237e-02   1.134   0.2574
year               1.375e+00  9.645e-02  14.261  < 2e-16 ***
factor(origin)2    2.588e+00  5.323e-01   4.861 1.71e-06 ***
factor(origin)3    2.453e+00  5.224e-01   4.695 3.73e-06 ***
displacement:year -3.560e-03  4.953e-04  -7.187 3.51e-12 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.107 on 382 degrees of freedom
Multiple R-squared:  0.8451,    Adjusted R-squared:  0.8415
F-statistic: 231.6 on 9 and 382 DF,  p-value: < 2.2e-16

多重共線性をチェック

多重共線性のチェックのためにVIF（Variance Inflation Factor）を計算。

VIFについてはこちらを参照。

car パッケージの vif() 関数を使う。

library(car) で呼び出せない場合、install.packages(“car”) で一回だけインストールを行う。

> library(car)
要求されたパッケージ carData をロード中です
>  vif(res1)
GVIF Df GVIF^(1/(2*Df))
cylinders      10.737771  1        3.276854
displacement   22.937950  1        4.789358
horsepower      9.957265  1        3.155513
weight         11.074349  1        3.327814
acceleration    2.625906  1        1.620465
year            1.301373  1        1.140777
factor(origin)  2.096060  2        1.203236

GVIFの列を確認する。

慣例として、5以上は多重共線性の可能性あり、10以上は多重共線性の可能性がかなり高いと判断する。

displacementが5に近く多重共線性の可能性を考え、外してみて再解析してみる。

GVIFが5に近いものはなくなった。

> res11 <- lm(mpg ~ cylinders + horsepower + weight + acceleration + year + factor(origin), data=Auto1)
> vif(res11)
GVIF Df GVIF^(1/(2*Df))
cylinders      6.249795  1        2.499959
horsepower     9.096327  1        3.016012
weight         9.260848  1        3.043164
acceleration   2.600476  1        1.612599
year           1.285826  1        1.133943
factor(origin) 1.794849  2        1.157463
> summary(res11)
Call:
lm(formula = mpg ~ cylinders + horsepower + weight + acceleration +
year + factor(origin), data = Auto1)
Residuals:
Min      1Q  Median      3Q     Max
-9.2846 -2.1094  0.0135  1.8127 13.4034
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)     -1.861e+01  4.726e+00  -3.939 9.71e-05 ***
cylinders        1.610e-01  2.479e-01   0.649 0.516474
horsepower      -5.554e-03  1.325e-02  -0.419 0.675378
weight          -5.880e-03  6.059e-04  -9.704  < 2e-16 ***
acceleration     4.882e-02  9.886e-02   0.494 0.621702
year             7.593e-01  5.206e-02  14.585  < 2e-16 ***
factor(origin)2  2.023e+00  5.383e-01   3.758 0.000198 ***
factor(origin)3  2.317e+00  5.316e-01   4.359 1.68e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.344 on 384 degrees of freedom
Multiple R-squared:  0.8197,    Adjusted R-squared:  0.8164
F-statistic: 249.4 on 7 and 384 DF,  p-value: < 2.2e-16

情報量規準でモデル診断

AIC（赤池情報量規準）、BIC（ベイズ情報量規準）の二つでモデル診断。

当てはまりの良さをチェック。

AIC(res1, res11, res2)
BIC(res1, res11, res2)

値が小さいほうが当てはまりがよい。

AICもBICも交互作用項を入れたモデルが最も当てはまりがよい。

> AIC(res1, res11, res2)
df      AIC
res1  10 2060.928
res11  9 2068.848
res2  11 2013.216
> BIC(res1, res11, res2)
df     BIC
res1  10 2100.64
res11  9 2104.59
res2  11 2056.90

まとめ

R の ISLR パッケージにある Auto データで、重回帰分析をやってみた。

順番としては、先行研究や理論をもとにモデルを作成し、残差プロットや情報量規準で当てはまりを診断する。

参考になれば。