EZR で対応のある 2 値カテゴリカルデータを群間比較する方法

対応のある２値データを群間比較したいときどうすればよいのか？

対応のある２値データの群間比較とはどういう状況か？

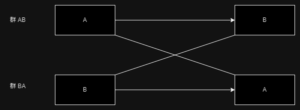
対応のある２値データの群間比較とはどういう状況だろうか。

それは介入前後で、Yes/Noとか、あり・なしとか、そういう２値のデータがあって、さらに介入が異なる群が複数存在する場合どうするかということである。

群間比較がなければマクネマー検定を実施したい状況である。

対応のある２値データを群間比較には一般化線形混合モデルを使う

対応のある２値データを群間比較する一つの方法は、一般化線形混合モデルを用いた方法である。

線形混合モデルは、対応ある連続データを複数回測定した場合のモデルで、それを２値の繰り返し測定にも対応したものが一般化線形混合モデルである。

対応のある２値データの群間比較サンプルデータ

対応ある２値データで群間比較できるサンプルデータを生成してみた。

一様分布のランダム変数を発生させて、50 例 2 群で、ありなし・YesNoなど 2 値の評価を、介入等の事前事後の 2 回繰り返した場合のサンプルデータを作成した。

下記は R のスクリプトだが、GLMM1.csvという名前で書き出し
ている。

書き出すパスは、PCの環境によって異なるので、~~~と書いている。

group <- c(rep(1,50),rep(2,50))
pre <- round(runif(100))
post <- round(runif(100))
dat <- data.frame(group, pre, post)
write.csv(dat, "C:\\Users\\~~~\\GLMM1.csv")

これを縦に積み重ねたデータセットを作成する必要がある。

以下はEZRにCSVファイルを取り込んだ後、縦に積み重ねたデータを作成した際のスクリプトを参考までに貼り付けている。

EZRでは、アクティブデータセット → 変数の操作 → 複数の変数を縦に積み重ねたデータセットを作成する メニューを用いると、縦に積み重ねたデータセットを作成できる。

#####複数の変数を縦に積み重ねたデータセットを作成する#####
TempDF <-  GLMM1
#Convert to long format
n <- length(TempDF[,1])
TempDF2 <- reshape(TempDF, varying=list(c("pre", "post")),
v.names="outcome", timevar="time", direction="long")
RepeatNumber <- c("pre", "post")
TempDF2$time <- RepeatNumber[TempDF2$time]
GLMMvert1 <- TempDF2
#####連続変数を因子に変換する#####
GLMMvert1$group <- as.factor(GLMMvert1$group)

対応のある２値データの群間比較を一般化線形混合モデルで実施する

EZRの標準メニューから、統計量 → モデルへの適合 → 一般化線形混合モデルと進むと解析できる。

最初にlibrary(lme4)で、lme4パッケージを呼び出しておく。

メニューから解析すると以下のスクリプトがRスクリプト窓に出力される。

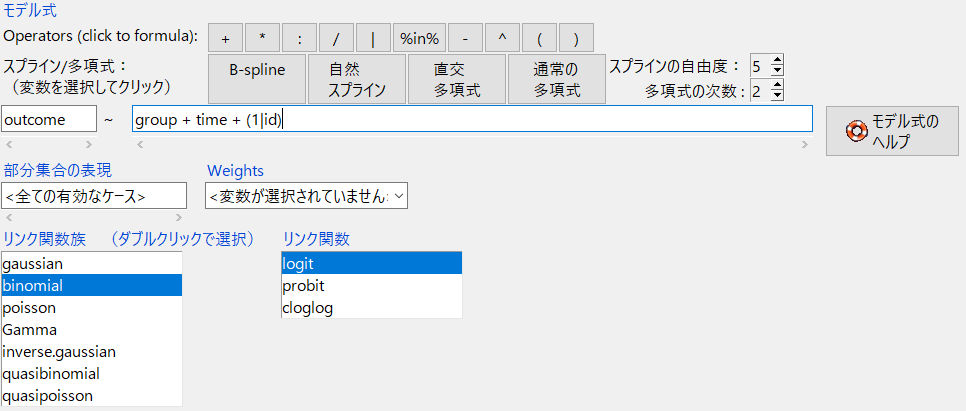
モデルの指定は、従属変数がoutcome, 独立変数側の枠には、group + time + (1|id) と書き入れる。

groupは群の変数、timeが前か後かの時点の変数、idは同一例であることを示す指標で、これが変量効果として投入されている。

library(lme4)
GLMM.2 <- glmer(outcome ~ group + time + (1 | id), family=binomial(logit),
data=GLMMvert1)
summary(GLMM.2)
exp(coef(GLMM.2))  # Exponentiated coefficients ("odds ratios")

結果のキモの部分は以下のとおりである。

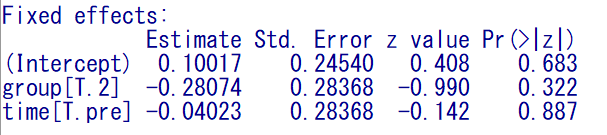
preとpostが逆になってしまっている。

postの推定値が出力されるように、アクティブデータセット → 変数の操作 → 因子水準を再順序化する メニューで変更しておくとよかった。

いずれにしても group の効果の検定と、time の効果の検定が同時に実施されている。

推定値をオッズ比に変更した値も計算される。

95 % 信頼区間は、confint() で計算して、真数変換 exp() で、算出できる（以下、GLMM.1 は上記の GLMM.2 と同じものである）

もしも、この方法で 95 ％ 信頼区間が計算できない場合は、以下のスクリプトを使って手動で計算することができる

se <- sqrt(diag(vcov(GLMM.1)))
upperCI <- exp(coef(GLMM.1) + 1.96*se)
lowerCI <- exp(coef(GLMM.1) - 1.96*se)

vcov は分散・共分散行列を求める関数、diag は行列の対角成分を抜き出す関数で、これで分散が取り出せて、平方根 sqrt を計算すると標準誤差が得られる

標準誤差に 1.96 かけた値を偏回帰係数の点推定値から引くと 95 ％ 信頼区間下限、足すと 95 ％ 信頼区間上限が計算される

計算結果は以下のとおり

上記の confint を使った時と、ほとんど同じ値になる

confint で計算できない場合は、簡易的にこちらの方法でよいと思われる

まとめ

対応のある２値データを群間比較したいとき、一般化線形混合モデルを使う方法がある。

ダミーのサンプルデータを用いて、EZRでのやり方を解説した。

おすすめ書籍

EZR公式マニュアル