相関係数は、相関関係の強さを示す指標。
一方が大きいときにもう一方が大きければ、正の相関関係で、相関係数は1に近い。
一方が大きいときにもう一方が小さい場合は、負の相関関係で相関係数は-1に近い。
では、偏相関係数とは何か?
違いは何か?
偏相関係数とは何か?
偏相関係数も、相関係数の一種である。
相関係数を計算する2つの変数と、ともに関係しているほかの要因の影響を除いた相関関係を見たい場合がある。
この時に、偏相関係数を計算する。
相関係数を計算した2変数とともに関連している別の第3の変数のために、相関関係が見えていたのかもしれない。
その見かけの相関関係を作っていた第3の変数の影響を除いた、真の相関関係を調べるのが、偏相関係数である。
では、どんなふうに計算するか?
偏相関係数を計算するサンプルデータ
Rに組み込みでついている airquality データを使う。
これは、1973年のNew Yorkのオゾン濃度と太陽放射、風速、気温、月、日のデータである。
このうち、オゾン濃度、風速、気温を使うことにする。
air1 <- airquality[,c(1,3,4)]
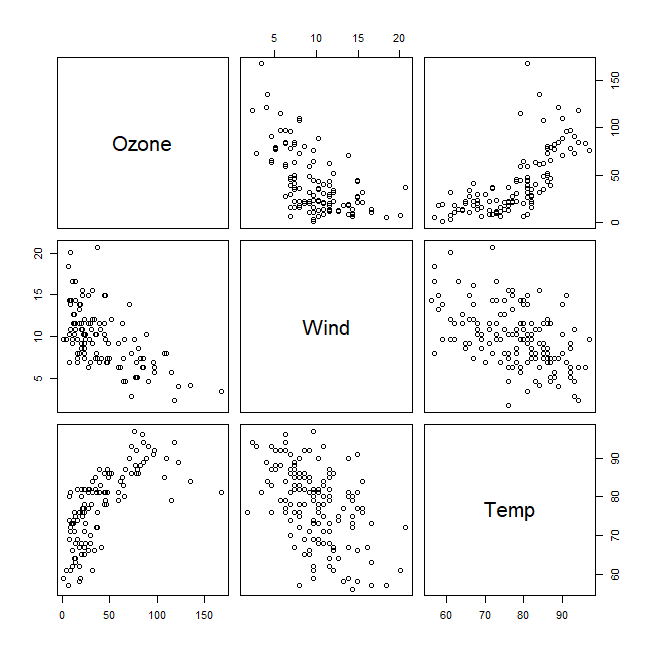
pairs(air1)
pairs()を使うと、いっぺんにたくさんの変数同士の散布図が描ける。
Ozone と Wind, Ozone と Temp、WindとTempの三つの散布図をXとYを変えて、2セット描いている。
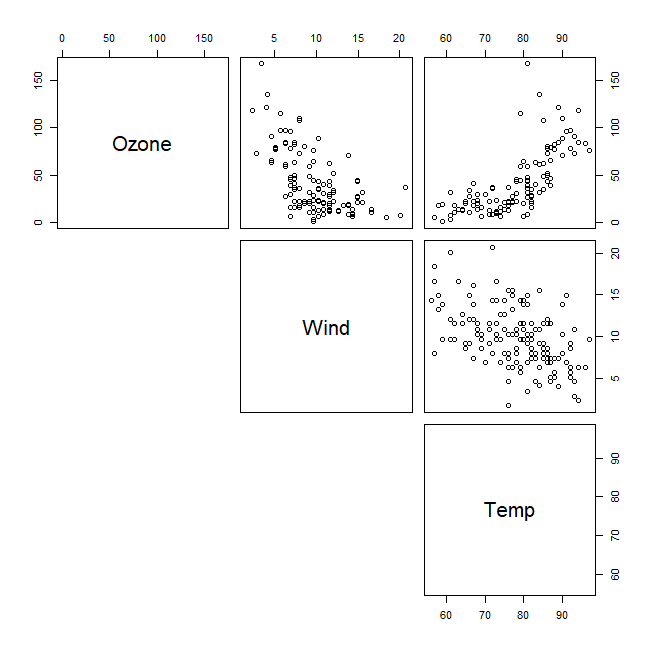
pairs(air1,lower.panel=NULL)
lower.panel=NULL もしくは upper.panel=NULL を使うと、下半分または上半分のグラフを消すことができる。
最初の変数、今回はオゾン濃度、との関係を中心的に見たいので、下半分を消して上半分だけにすると見やすいかもしれない。
相関係数はどうやって計算するか?
Rの関数を使う場合
Rではcor()を使うと、計算できる。
欠損値 NA がある場合は、use=で調整する。
ペアでNAを削除して計算する場合は pairwise.complete.obs を使う。
すべての変数で、NAが一つでもあるデータ行は削除する場合は complete.obs を使う。
cor(air1,use="pairwise.complete.obs")
右上に向かっているプロットの組み合わせはプラスの値が計算されている(OzoneとTempなど)。
右下に向かっているプロットの場合はマイナスの値だ(OzoneとWindなど)
> cor(air1,use="pairwise.complete.obs")
Ozone Wind Temp
Ozone 1.0000000 -0.6015465 0.6983603
Wind -0.6015465 1.0000000 -0.4579879
Temp 0.6983603 -0.4579879 1.0000000相関係数をStep by stepで計算してみる
相関係数は、二つの変数XとYの共変動をXとYの変動の平方根で割ると計算できる。
変動は平均との差を二乗したものの合計。
共変動はXの平均との差とYの平均との差を二乗せずに掛け合わせたものの合計。
Xの変動とYの変動がまったく同じなら、共変動も同一になり、割ると1になる。
XとYが真逆なら、共変動は符号が逆になり、-1となる。
通常は、-1と1の中間になる。これが相関係数だ。
airquality データの Wind と Temp の相関係数を関数を使わずに求めてみる。
Wind <- air1$Wind
Temp <- air1$Temp
m.Wind <- mean(air1$Wind)
m.Temp <- mean(air1$Temp)
sum((Wind-m.Wind)*(Temp-m.Temp))/(sqrt(sum((Wind-m.Wind)^2))*sqrt(sum((Temp-m.Temp)^2)))
cor()を使った時の結果行列における、WindとTempの交点の値と同じことがわかる。
> sum((Wind-m.Wind)*(Temp-m.Temp))/(sqrt(sum((Wind-m.Wind)^2))*sqrt(sum((Temp-m.Temp)^2)))
[1] -0.4579879
偏相関係数はどうやって計算するか?
Rの関数を使う場合
ppcor パッケージを使う。ppcor パッケージは最初の一回だけインストールして使う。
install.packages("ppcor")
library()で呼び出してから使用する。
偏相関係数は、三つの変数すべて欠損値がないデータ行だけに限って計算する。
欠損値があると計算ができない。
library(ppcor)
air2 <- subset(air1, complete.cases(air1))
cor(air2)
欠損値がないデータにすると、pairwise.complete.obs のときと若干値が変わった。
大きな違いはない。
> cor(air2)
Ozone Wind Temp
Ozone 1.0000000 -0.6015465 0.6983603
Wind -0.6015465 1.0000000 -0.5110750
Temp 0.6983603 -0.5110750 1.0000000pcor()で偏相関係数を計算する。
pcor(air2)
結果は、以下の通り。
OzoneとWind、WindとTempの相関係数($estimateの行列を見る)の絶対値が相対的に小さくなっているのがわかる。
> pcor(air2)
$estimate
Ozone Wind Temp
Ozone 1.0000000 -0.3976400 0.5693387
Wind -0.3976400 1.0000000 -0.1591191
Temp 0.5693387 -0.1591191 1.0000000
$p.value
Ozone Wind Temp
Ozone 0.000000e+00 1.080046e-05 3.149109e-11
Wind 1.080046e-05 0.000000e+00 8.940196e-02
Temp 3.149109e-11 8.940196e-02 0.000000e+00
$statistic
Ozone Wind Temp
Ozone 0.000000 -4.606844 7.361793
Wind -4.606844 0.000000 -1.713287
Temp 7.361793 -1.713287 0.000000
$n
[1] 116
$gp
[1] 1
$method
[1] "pearson"
偏相関係数を Step by stepで計算してみる
Tempで説明できる部分を除いたOzoneと、Tempで説明できる部分を除いたWindとの相関係数を計算すると、Tempの影響を除いたOzoneとWindの偏相関係数になる。
Temp2 <- air2$Temp
Ozone2 <- air2$Ozone
Wind2 <- air2$Wind
rho.yz <- cor(Ozone2,Wind2)
rho.xy <- cor(Temp2,Ozone2)
rho.xz <- cor(Temp2,Wind2)
(rho.yz - rho.xy*rho.xz)/(sqrt(1-rho.xy^2)*sqrt(1-rho.xz^2))
WindとOzoneの相関係数はもともとー0.602だった。
WindもOzoneもTempと相関があった。
WindとTempの相関係数はー0.511、OzoneとTempは0.698だった。
Tempの影響を除いたWindとOzoneの偏相関係数は、-0.398になり、絶対値で考えれば小さくなり関連が弱くなった。
最初のー0.602は見かけの分が含まれていて、Tempとの相関分が上乗せされていたと言える。
> (rho.yz - rho.xy*rho.xz)/(sqrt(1-rho.xy^2)*sqrt(1-rho.xz^2))
[1] -0.39764
結局OzoneとTempがもっとも強い相関関係で、Windの影響を除いたTempとOzoneの偏相関係数は0.569であった。
順位相関係数はどんなときに使うか?
通常、相関係数と言った場合、Pearson(ピアソン)の積率相関係数を言っている。連続量をそのまま連続量として扱う相関係数だ。
散布図を描いてみた時に、直線の関係ではなく、曲線の関係に見えるときがある。
今回のOzoneとWind、OzoneとTempの場合も、曲線関係に見える。
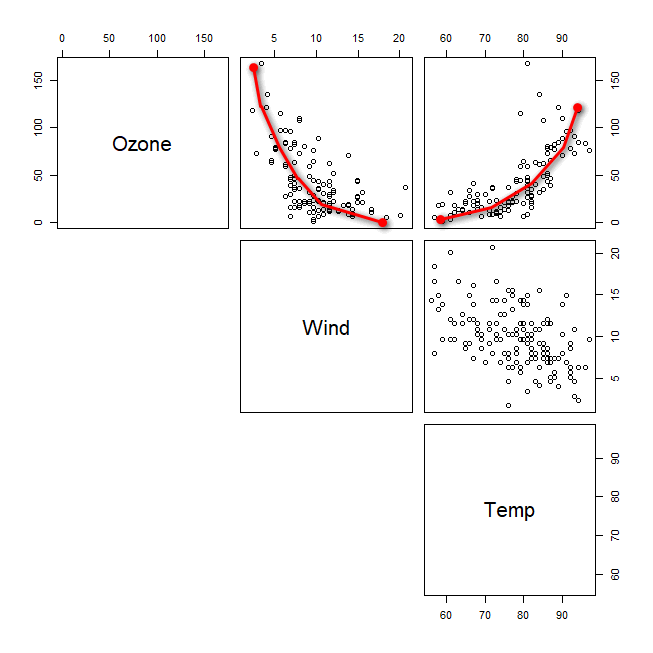
相関関係が直線ではない場合に、いい方法がある。
数値を順序(順位)に置き換えて相関係数を計算する方法だ。
順位であると、直線的な関係かどうかは気にしなくてよい。
Spearman(スピアマン)の順位相関係数と言う。
順位相関係数を使いたい場合はどうすればいいか?
Rの関数を使う方法
順位相関係数は、先ほどと同じcor()を使える。cor()に、method=”spearman”を追加する。
cor(air2,method="spearman")
OzoneとTempの順位相関係数は、上記の積率相関係数に比べて高い値(0.774)だ。
順位相関係数のほうがより適切なのかもしれない。
> cor(air2,method="spearman")
Ozone Wind Temp
Ozone 1.0000000 -0.5901551 0.7740430
Wind -0.5901551 1.0000000 -0.5178411
Temp 0.7740430 -0.5178411 1.0000000偏相関係数も計算してみる。
pcor()に、method=”spearman”を追加する。
pcor(air2, method="spearman")
やはり、OzoneとTempの偏相関係数は、積率相関係数よりも、順位相関係数のほうが高い(0.678)。
これはますます順位相関係数のほうが適切なのかもと思えてきた。
> pcor(air2, method="spearman")
$estimate
Ozone Wind Temp
Ozone 1.0000000 -0.3495442 0.6782860
Wind -0.3495442 1.0000000 -0.1194151
Temp 0.6782860 -0.1194151 1.0000000
$p.value
Ozone Wind Temp
Ozone 0.000000e+00 0.0001286614 8.235308e-17
Wind 1.286614e-04 0.0000000000 2.036758e-01
Temp 8.235308e-17 0.2036757725 0.000000e+00
$statistic
Ozone Wind Temp
Ozone 0.000000 -3.965874 9.812601
Wind -3.965874 0.000000 -1.278549
Temp 9.812601 -1.278549 0.000000
$n
[1] 116
$gp
[1] 1
$method
[1] "spearman"順序相関係数を Step by stepで計算する方法
それぞれの値を順位に置き換えるためrank()を使う。そして、それぞれの平均値を計算しておく。
r.Ozone <- rank(air2$Ozone)
r.Wind <- rank(air2$Wind)
r.Temp <- rank(air2$Temp)
m.r.Ozone <- mean(r.Ozone)
m.r.Wind <- mean(r.Wind)
m.r.Temp <- mean(r.Temp)
OzoneとTempの順位相関係数を計算する。
sum((r.Ozone-m.r.Ozone)*(r.Temp-m.r.Temp))/(sqrt(sum((r.Ozone-m.r.Ozone)^2))*sqrt(sum((r.Temp-m.r.Temp)^2)))
計算結果はcor()にmethod=”spearman”を使った結果と同じだ。
> sum((r.Ozone-m.r.Ozone)*(r.Temp-m.r.Temp))/(sqrt(sum((r.Ozone-m.r.Ozone)^2))*sqrt(sum((r.Temp-m.r.Temp)^2)))
[1] 0.774043
三つの変数それぞれ同士の順位相関係数を計算した後、偏相関係数を計算する。
(rho.r.WO <- cor(r.Wind,r.Ozone))
(rho.r.WT <- cor(r.Wind,r.Temp))
(rho.r.OT <- cor(r.Ozone,r.Temp))
順位に変換してcor()で相関係数を計算すると、cor()にmethod=”spearman”を使った結果と同じになる。
> (rho.r.WO <- cor(r.Wind,r.Ozone))
[1] -0.5901551
> (rho.r.WT <- cor(r.Wind,r.Temp))
[1] -0.5178411
> (rho.r.OT <- cor(r.Ozone,r.Temp))
[1] 0.774043
今回はOzoneとTempの偏相関係数を求めてみる。
(rho.r.OT-rho.r.WO*rho.r.WT)/(sqrt(1-rho.r.WO^2)*sqrt(1-rho.r.WT^2))
pcor()にmethod=”spearman”を使った結果と同じになった。
> (rho.r.OT-rho.r.WO*rho.r.WT)/(sqrt(1-rho.r.WO^2)*sqrt(1-rho.r.WT^2))
[1] 0.678286
まとめ
相関係数と偏相関係数の違いについて説明した。
また、Rで計算してみた。
cor()とpcor()があり、簡単に計算できる。
簡単に計算できる関数を使わずに、Step by stepで計算も可能だ。
また、散布図を描いた時に直線的でない相関関係に見えた場合は、順位相関係数を考慮する。
method=”spearman”を指定すれば、簡単に計算できる。
偏相関係数も計算できる。








コメント
コメント一覧 (1件)
[…] […]