R で薬剤経済分析を行う方法

薬剤経済学は、薬剤の持つ効力を、経済で測って吟味する学問。

新薬につけた薬価が、本当にその薬価に見合った効果を発揮しているかを吟味し、政策に生かそうとする学問。

薬剤経済学の書籍にそって実践してみる

ネタ元は、坂巻弘之 著　やさしく学ぶ薬剤経済学

本稿は、ネタ本の内容を写経したに過ぎないので、詳細についてはネタ本を確認されたい。

判断分析モデル Decision analysis model その1（Exercise 5）

参考文献：

Evans KW, et al: Pharmacoeconomics 1997;12(5):567-577.

条件設定したのちに、

1. “有効-完全消失”
2. “有効-再発-消失”
3. “無効-放置-消失”
4. “無効-緊急入院-自然消失”
5. “無効-緊急入院-加療-消失”

という5つのシナリオについて、効用値とコストを見積もり、費用対効果を計算する。

そして、C/F群とA群との比較を行う。

# C/F群
CF.eff <- 0.38 #有効率
CF.rec <- 0.30 #再発率
CF.ineff <- 1-0.38 #無効率
CF.ineff.ER <- 0.08 #無効時緊急入院率
CF.ineff.ER.eff <- 0.998 #無効時緊急入院後自然消失率
# 初期治療 有効率
p1.CF <- 0.38
p1.AA <- 0.56
# 初期治療 無効率
q1.CF <- 0.62
q1.AA <- 0.44
# 再発率 再発なく完全消失の割合
p2.CF <- 0.70
p2.AA <- 0.60
# 再発率 再発 同治療後消失の割合
q2.CF <- 0.30
q2.AA <- 0.40
# 無効時 緊急入院率
p3.CF <- 0.08
p3.AA <- 0.08
# 無効時 放置 自然消失の割合
q3.CF <- 0.92
q3.AA <- 0.92
# 入院後経過 自然消失の割合
p4.CF <- 0.998
p4.AA <- 0.998
# 入院後経過 入院加療で消失する割合
q4.CF <- 0.002
q4.AA <- 0.002
# 初期治療の費用
C1.CF <- 1.32
C1.AA <- 16.10
# 再発治療（同治療）の費用
C2.CF <- 1.32
C2.AA <- 16.10
# 緊急入院の費用
C3.CF <- 63.13
C3.AA <- 63.13
# 入院加療の費用
C4.CF <- 1093.00
C4.AA <- 1093.00
scenari <- c(
"有効-完全消失",
"有効-再発-消失",
"無効-放置-消失",
"無効-緊急入院-自然消失",
"無効-緊急入院-加療-消失")
utility <- c(1.0, 0.9, -0.3, 0.1, -0.3) #効用値の割り当て

まずC/F群の計算。

prob.CF <- c(
  p1.CF*p2.CF,
  p1.CF*q2.CF,
  q1.CF*q3.CF,
  q1.CF*p3.CF*p4.CF,
  q1.CF*p3.CF*q4.CF)
cost.CF <- c(
  C1.CF,
  C1.CF+C2.CF,
  C1.CF,
  C1.CF+C3.CF,
  C1.CF+C4.CF)
data.frame(scenari, utility, prob.CF, cost.CF)

データセットを表示。

> data.frame(scenari, utility, prob.CF, cost.CF)
scenari utility   prob.CF cost.CF
1           有効-完全消失     1.0 0.2660000    1.32
2          有効-再発-消失     0.9 0.1140000    2.64
3          無効-放置-消失    -0.3 0.5704000    1.32
4  無効-緊急入院-自然消失     0.1 0.0495008   64.45
5 無効-緊急入院-加療-消失    -0.3 0.0000992 1094.32

効用の期待値を計算する。

est.util.CF <- prob.CF*utility
sum(est.util.CF)

効用の期待値の合計は約0.20と計算される。

> sum(est.util.CF)
[1] 0.2024003

費用の期待値を計算する。

est.cost.CF <- prob.CF*cost.CF
sum(est.cost.CF)

費用の期待値の合計は約4.7と計算される。

> sum(est.cost.CF)
[1] 4.703891

費用の期待値の合計と効用の期待値の合計の比を平均費用/効用比と言う。

> sum(est.cost.CF)/sum(est.util.CF)
[1] 23.24053

次にA群の計算。

prob.AA <- c(
  p1.AA*p2.AA,
  p1.AA*q2.AA,
  q1.AA*q3.AA,
  q1.AA*p3.AA*p4.AA,
  q1.AA*p3.AA*q4.AA)
cost.AA <- c(
  C1.AA,
  C1.AA+C2.AA,
  C1.AA,
  C1.AA+C3.AA,
  C1.AA+C4.AA)
data.frame(scenari, utility, prob.AA, cost.AA)

データセットを表示する。

> data.frame(scenari, utility, prob.AA, cost.AA)
scenari utility   prob.AA cost.AA
1           有効-完全消失     1.0 0.3360000   16.10
2          有効-再発-消失     0.9 0.2240000   32.20
3          無効-放置-消失    -0.3 0.4048000   16.10
4  無効-緊急入院-自然消失     0.1 0.0351296   79.23
5 無効-緊急入院-加療-消失    -0.3 0.0000704 1109.10

効用の期待値合計、費用の期待値合計を計算し、費用対効用の比を取る。

# 効用の期待値
est.util.AA <- prob.AA*utility
# 費用の期待値
est.cost.AA <- prob.AA*cost.AA
# 平均費用/効用比
sum(est.cost.AA)/sum(est.util.AA)

費用と効用の期待値合計同士の比は、平均費用/効用比と呼ぶ。

> sum(est.cost.AA)/sum(est.util.AA)
[1] 52.42698

C/F群は、23.24053だったのに対し、A群は、52.42698と倍以上の費用対効用比。

よって、C/F群のほうが、費用対効用比が低く抑えられていると言える。

判断分析モデル Decision analysis model その2（Exercise 6）

新薬を使った場合と従来薬を使った場合の費用と効果の増分を、副作用あり・なしともに含めてのシナリオ全体で計算する。

まず、共通の条件設定。下痢や肝機能障害の副作用の条件。

treat.day <- 84
dia.admit <- 0.70
dia.cost.o <- 150
dia.cost.a <- 20000
liv.cost.a <- 30000

A（新薬を使った場合）、B（従来の場合） 2つの条件。

副作用が起きる可能性やコストのパターン。

survival <- c(0.35,0.20)
diarrhea <- c(0.02,0.10)
liverdys <- c(0.15,0.01)
can.cost <- c(2875,2500)
livertes <- c(1500,1000)

4つのシナリオ。

1. 副作用なし
2. 下痢の副作用あり外来で治療
3. 下痢の副作用あり入院して元の治療は中止
4. 肝機能障害発生

の4つ。

それぞれに合わせてコストの算出。

scenario <- c("副作用なし","下痢外来加療","下痢入院加療治療中止","肝機能障害")
total.cost <- rbind(
  (can.cost+livertes)*treat.day,
  (can.cost+livertes+dia.cost.o)*treat.day,
  (can.cost+livertes)*14+(dia.cost.o+dia.cost.a)*14,
  (can.cost+livertes)*treat.day+liv.cost.a*28
)
colnames(total.cost) <- c("A","B")
rownames(total.cost) <- scenario
total.cost

コストの合計額を表示するとこうなる。

> total.cost
                           A       B
副作用なし            367500  294000
下痢外来加療          380100  306600
下痢入院加療治療中止  343350  331100
肝機能障害           1207500 1134000

4つのシナリオそれぞれが起きる確率を計算。

probabilit <- rbind(
  1-diarrhea-liverdys,
  diarrhea*(1-dia.admit),
  diarrhea*dia.admit,
  liverdys
)
colnames(probabilit) <- c("A","B")
rownames(probabilit) <- scenario
probabilit

4つのシナリオが起きる確率は以下の通り。

> probabilit
                         A    B
副作用なし           0.830 0.89
下痢外来加療         0.006 0.03
下痢入院加療治療中止 0.014 0.07
肝機能障害           0.150 0.01

コストと生じうる確率をかけると、期待費用が算出できる。

> total.cost * probabilit
                            A      B
副作用なし           305025.0 261660
下痢外来加療           2280.6   9198
下痢入院加療治療中止   4806.9  23177
肝機能障害           181125.0  11340

縦方向に合計すると、患者一人当たりの期待費用が計算できる。

list("患者1人当たり期待費用"=colSums(total.cost * probabilit))

Aだと50万近く、Bだと30万ちょっとになる。

> list("患者1人当たり期待費用"=colSums(total.cost * probabilit))
$患者1人当たり期待費用
       A        B 
493237.5 305375.0 

費用/効果比は、患者一人当たりの期待費用を生存割合で割る。

> list("費用/効果比"=colSums(total.cost * probabilit)/survival)
$`費用/効果比`
      A       B 
1409250 1526875 

従来の治療から新しい治療になって、どれだけ費用対効果が増したかを計算する。

患者一人当たりの期待費用を差分を、生存割合の差分で割り算すると、増分費用/効果比が計算される。

inc.cost <- colSums(total.cost * probabilit)
inc.rati <- (inc.cost[1]-inc.cost[2])/(survival[1]-survival[2])
names(inc.rati) <- "増分費用/効果比"
inc.rati

増分費用/効果比がどれだけなら、意味合いがあるとするかが、新薬の意味合いにかかってくる。

例題では、125万超。

> inc.rati
増分費用/効果比 
        1252417 

マルコフモデル Markov model その1（Exercise 8）

マルコフモデルとは、現在の状態からのみ次の状態が発生するという考えのもと、時間とともに変化する確率モデルのことである。

ある病前状態があり、次の中等度の疾病にかかり、その次のもっと重篤な疾病にかかり、最終的に死を迎えるような生活習慣病の考え方にあてはめやすいモデルといえる。

ここでは、高脂血症の患者さんが、狭心症にかかり、心筋梗塞にかかり、死を迎えるシミュレーションを行う。

S1 <- c(0.90,0.00,0.00,0.00)
S2 <- c(0.06,0.83,0.88,0.00)
S3 <- c(0.04,0.12,0.05,0.00)
S4 <- c(0.00,0.05,0.07,1.00)

上記条件で、マルコフ連鎖計算をする。

my.markov <- function(n){
  nu <- c(100,0,0,0)
  dat.nu <- nu
  S <- matrix(c(S1,S2,S3,S4),nr=4)
  for (i in 1:n){
    nu <- nu%*%S
    dat.nu <- rbind(dat.nu,nu)
  }
  dat.nu
}

マルコフ連鎖を20回計算してみる。

dat <- my.markov(20)
colnames(dat) <- c("高脂血症","狭心症","心筋梗塞","死")
dat

どの状態がどのように増えていくのかのシミュレーション。

> dat
        高脂血症   狭心症 心筋梗塞        死
dat.nu 100.00000  0.00000 0.000000  0.000000
        90.00000  6.00000 4.000000  0.000000
        81.00000 13.90000 4.520000  0.580000
        72.90000 20.37460 5.134000  1.591400
        65.61000 25.80284 5.617652  2.969510
        59.04900 30.29649 6.001623  4.652888
        53.14410 33.97045 6.297620  6.587826
        47.82969 36.92603 6.517100  8.727182
        43.04672 39.25343 6.670166 11.029680
        38.74205 41.03290 6.765789 13.459263
        34.86784 42.33572 6.811919 15.984514
        31.38106 43.22521 6.815597 18.578134
        28.24295 43.75751 6.783047 21.216486
        25.41866 43.98239 6.719772 23.879175
        22.87679 43.94391 6.630622 26.548679
        20.58911 43.68100 6.519872 29.210018
        18.53020 43.22806 6.391278 31.850459
        16.67718 42.61543 6.248139 34.459251
        15.00946 41.86980 6.093346 37.027392
        13.50852 41.01464 5.929422 39.547417
        12.15767 40.07056 5.758569 42.013208

図にしてみるとこうなる。

matplot(dat)

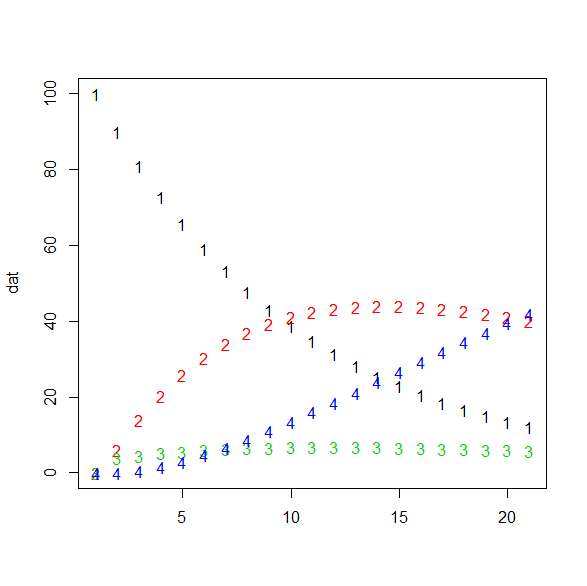
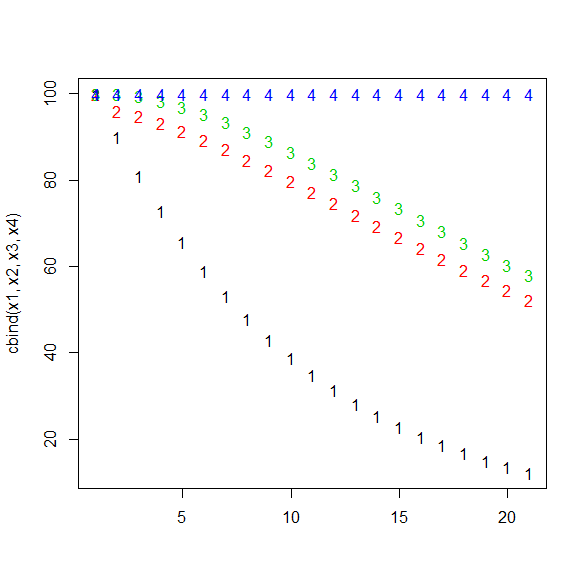
積み上げ計算をしたグラフにすると、

x1 <- dat[,1]
x2 <- x1+dat[,2]
x3 <- x2+dat[,3]
x4 <- x3+dat[,4]
matplot(cbind(x1,x2,x3,x4))

こうなる。

マルコフモデル Markov model その2（Exercise 9）

条件が2つあった場合の比較を行ってみる。SaとSbの2つの条件があったとする。

Sa1 <- c(0.90,0.00,0.00,0.00)
Sa2 <- c(0.06,0.83,0.88,0.00)
Sa3 <- c(0.04,0.12,0.05,0.00)
Sa4 <- c(0.00,0.05,0.07,1.00)
Sb1 <- c(0.93,0.00,0.00,0.00)
Sb2 <- c(0.05,0.85,0.90,0.00)
Sb3 <- c(0.02,0.10,0.03,0.00)
Sb4 <- c(0.00,0.05,0.07,1.00)

2 つのマルコフ連鎖モデルの計算スクリプトを作成する。

my.markovA <- function(n){
  nu <- c(100,0,0,0)
  dat.nu <- nu
  S <- matrix(c(Sa1,Sa2,Sa3,Sa4),nr=4)
  for (i in 1:n){
    nu <- nu%*%S
    dat.nu <- rbind(dat.nu,nu)
  }
  dat.nu
}

my.markovB <- function(n){
  nu <- c(100,0,0,0)
  dat.nu <- nu
  S <- matrix(c(Sb1,Sb2,Sb3,Sb4),nr=4)
  for (i in 1:n){
    nu <- nu%*%S
    dat.nu <- rbind(dat.nu,nu)
  }
  dat.nu
}

2つの条件のマルコフ連鎖解析を行う。

新たな死亡だけをデータセットに残す。

datA <- my.markovA(20)
colnames(datA) <- c("高脂血症","狭心症","心筋梗塞","死")
last.yr.deathA <- c(0,datA[1:20,4])
datB <- my.markovB(20)
colnames(datB) <- c("高脂血症","狭心症","心筋梗塞","死")
last.yr.deathB <- c(0,datB[1:20,4])
datA1 <- data.frame(datA,last.yr.deathA)
datA1$新たな死 <- datA1$死 - datA1$last.yr.deathA
datB1 <- data.frame(datB,last.yr.deathB)
datB1$新たな死 <- datB1$死 - datB1$last.yr.deathB
datA1 <- datA1[,c(1,2,3,6)]
datB1 <- datB1[,c(1,2,3,6)]

A群のデータは以下のように算出された。

> datA1
        高脂血症   狭心症 心筋梗塞 新たな死
dat.nu 100.00000  0.00000 0.000000 0.000000
X       90.00000  6.00000 4.000000 0.000000
X.1     81.00000 13.90000 4.520000 0.580000
X.2     72.90000 20.37460 5.134000 1.011400
X.3     65.61000 25.80284 5.617652 1.378110
X.4     59.04900 30.29649 6.001623 1.683378
X.5     53.14410 33.97045 6.297620 1.934938
X.6     47.82969 36.92603 6.517100 2.139356
X.7     43.04672 39.25343 6.670166 2.302498
X.8     38.74205 41.03290 6.765789 2.429583
X.9     34.86784 42.33572 6.811919 2.525250
X.10    31.38106 43.22521 6.815597 2.593621
X.11    28.24295 43.75751 6.783047 2.638352
X.12    25.41866 43.98239 6.719772 2.662689
X.13    22.87679 43.94391 6.630622 2.669504
X.14    20.58911 43.68100 6.519872 2.661339
X.15    18.53020 43.22806 6.391278 2.640441
X.16    16.67718 42.61543 6.248139 2.608793
X.17    15.00946 41.86980 6.093346 2.568141
X.18    13.50852 41.01464 5.929422 2.520024
X.19    12.15767 40.07056 5.758569 2.465792

B群は以下の通り。

> datB1
        高脂血症   狭心症 心筋梗塞 新たな死
dat.nu 100.00000  0.00000 0.000000 0.000000
X       93.00000  5.00000 2.000000 0.000000
X.1     86.49000 10.70000 2.420000 0.390000
X.2     80.43570 15.59750 2.872400 0.704400
X.3     74.80520 19.86482 3.254636 0.980943
X.4     69.56884 23.55453 3.580225 1.221066
X.5     64.69902 26.72199 3.854236 1.428342
X.6     60.17009 29.41746 4.081807 1.605896
X.7     55.95818 31.68697 4.267602 1.756599
X.8     52.04111 33.57268 4.415889 1.883081
X.9     48.39823 35.11313 4.530566 1.987746
X.10    45.01035 36.34358 4.615195 2.072796
X.11    41.85963 37.29624 4.673021 2.140243
X.12    38.92946 38.00050 4.707007 2.191923
X.13    36.20439 38.48321 4.719850 2.229516
X.14    33.67009 38.76881 4.714004 2.254550
X.15    31.31318 38.87960 4.691703 2.268421
X.16    29.12126 38.83585 4.654974 2.272399
X.17    27.08277 38.65601 4.605659 2.267641
X.18    25.18698 38.35684 4.545426 2.255197
X.19    23.42389 37.95355 4.475786 2.236022

コストを定義する。

cost <- c(100,300,750,2500)
names(cost) <- c("高脂血症","狭心症","心筋梗塞","死亡")

それぞれの病態にコストを掛け合わせる。

datA2 <- cbind("高脂血症"=datA1[,1]*cost[1],
               "狭心症"=datA1[,2]*cost[2],
               "心筋梗塞"=datA1[,3]*cost[3],
               "新たな死亡"=datA1[,4]*cost[4])
datB2 <- cbind("高脂血症"=datB1[,1]*cost[1],
               "狭心症"=datB1[,2]*cost[2],
               "心筋梗塞"=datB1[,3]*cost[3],
               "新たな死亡"=datB1[,4]*cost[4])

A群とB群、それぞれのコストを計算する。

> datA2
       高脂血症    狭心症 心筋梗塞 新たな死亡
 [1,] 10000.000     0.000    0.000      0.000
 [2,]  9000.000  1800.000 3000.000      0.000
 [3,]  8100.000  4170.000 3390.000   1450.000
 [4,]  7290.000  6112.380 3850.500   2528.500
 [5,]  6561.000  7740.851 4213.239   3445.275
 [6,]  5904.900  9088.947 4501.217   4208.444
 [7,]  5314.410 10191.136 4723.215   4837.345
 [8,]  4782.969 11077.809 4887.825   5348.390
 [9,]  4304.672 11776.030 5002.625   5756.246
[10,]  3874.205 12309.870 5074.342   6073.958
[11,]  3486.784 12700.717 5108.939   6313.125
[12,]  3138.106 12967.563 5111.697   6484.051
[13,]  2824.295 13127.254 5087.286   6595.881
[14,]  2541.866 13194.718 5039.829   6656.722
[15,]  2287.679 13183.172 4972.967   6673.759
[16,]  2058.911 13104.299 4889.904   6653.347
[17,]  1853.020 12968.418 4793.458   6601.102
[18,]  1667.718 12784.628 4686.105   6521.981
[19,]  1500.946 12560.940 4570.009   6420.353
[20,]  1350.852 12304.393 4447.066   6300.060
[21,]  1215.767 12021.167 4318.927   6164.479

年あたりの合計コストと、20年間のトータルコストを計算する。

sum.year.costA <- matrix(c(datA1[,1],datA1[,2],datA1[,3],datA1[,4]),nc=4)%*%matrix(cost,nr=4)
sum.tota.costA <- sum(sum.year.costA)
sum.year.costB <- matrix(c(datB1[,1],datB1[,2],datB1[,3],datB1[,4]),nc=4)%*%matrix(cost,nr=4)
sum.tota.costB <- sum(sum.year.costB)

コストはBのほうがAよりも59000ほど安くなる。

> sum.tota.costA
[1] 500944.6
> sum.tota.costB
[1] 442204.8
> sum.tota.costA - sum.tota.costB
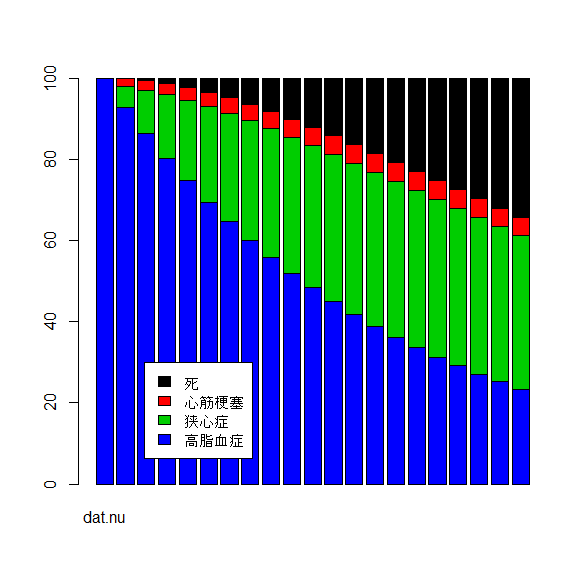
[1] 58739.81

マルコフモデルで予測したA群とB群を積み上げグラフで描画してみると、以下のとおりのグラフになる。

B群のほうが高脂血症でとどまる人が多い。

barplot(t(datA),col=c(4:1))
legend(3,30,c("死","心筋梗塞","狭心症","高脂血症"),bg="white",fill=c(1:4))
barplot(t(datB),col=c(4:1))
legend(3,30,c("死","心筋梗塞","狭心症","高脂血症"),bg="white",fill=c(1:4))

• GroupA

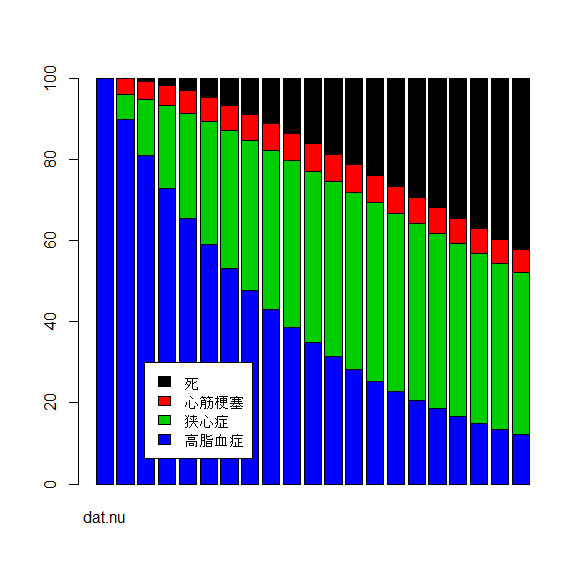
• GroupB

コストの積み上げグラフはこちら。

barplot(t(datA2),col=c(4:1))
legend(3,7000,c("新しい死亡","心筋梗塞","狭心症","高脂血症"),bg="white",fill=c(1:4))
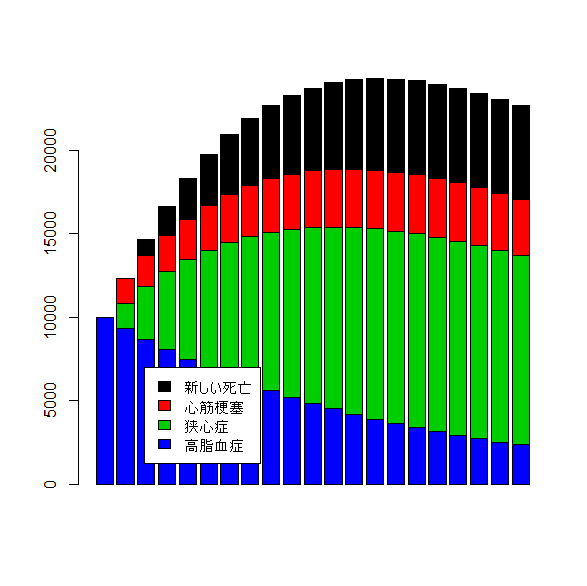
barplot(t(datB2),col=c(4:1))
legend(3,7000,c("新しい死亡","心筋梗塞","狭心症","高脂血症"),bg="white",fill=c(1:4))

• Cost of GroupA

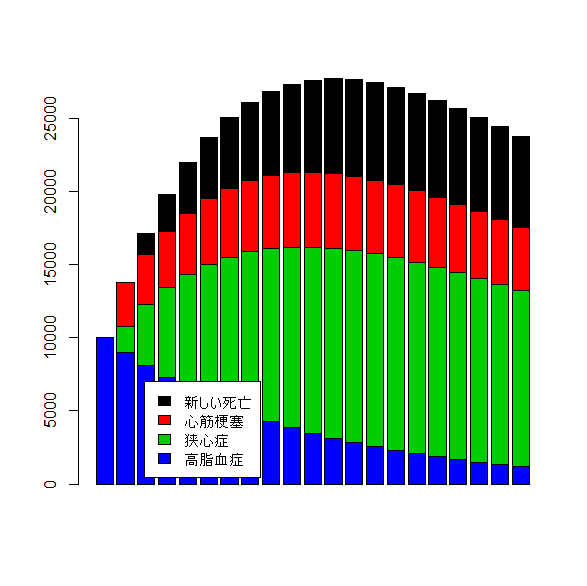
• Cost of GroupB

まとめ

統計ソフトRを使って、判断分析2例とマルコフモデル2例を、ネタ本の通りに提示した。

政策判断のエビデンスを作る方法論の基礎的な内容と言える。

ネタ本の内容を写経したに過ぎないので、詳細についてはネタ本を確認されたい。

参考書籍

やさしく学ぶ薬剤経済学