偏相関係数について。
順位相関係数は偏相関係数が計算できるか。
目次
偏相関係数が計算したい場面
新規の検査値Aと既存の検査値Bの関連性を検討したい。
nは40例程度。
解析するに当たり、患者背景が問題になると思っている。
既存の検査値 Bと身長が関連することが知られており(相関係数0.7)、AとBの関連性を検討するためには、身長で補正する必要があると思う。
新規の検査値 Aと身長は有意な相関がある(相関係数0.4)。
データはすべて連続変数のため、二変量の相関をピアソンの相関係数で検討したい。
偏相関で制御変数に身長を入れればよいのか?
また、既存の検査値 B が正規分布していないと思われるのだが、このような場合、ピアソンではなくスピアマンの順位相関係数で検討すべきだろうか?
その際、Spearmanの順位相関係数は、偏相関係数を計算できるか?
偏相関係数を計算するにあたり注意事項
偏相関で制御変数に身長を入れる方法は、解析方法の一つとして適切と思う。
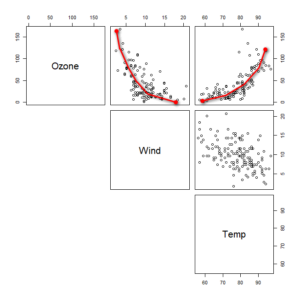
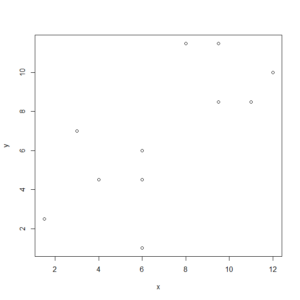
ピアソンかスピアマンかを選択する前に、まず散布図を眺めるのがよいだろう。
散布図を眺めて、直線的な関係が想定できれば、ピアソンの積率相関係数が適切だろう。
直線的な関係ではなさそうであれば、スピアマンの順位相関係数のほうがよいだろう。
スピアマンの順位相関係数でも、偏相関係数を計算できる。
こちらの記事を参照のこと。
あわせて読みたい

R で相関係数と偏相関係数の違いについて ピアソンとスピアマンの両方について
相関係数は、相関関係の強さを示す指標。 一方が大きいときにもう一方が大きければ、正の相関関係で、相関係数は1に近い。 一方が大きいときにもう一方が小さい場合は、…
まとめ
相関係数を計算したい場面で、背景因子の調整をしたい場合は、偏相関係数を計算するのがよい。
その際、ピアソンかスピアマンかは、散布図を見て決める。
ピアソンでもスピアマンでも偏相関係数は計算できる。
参考になれば。





コメント