ポアソン回帰を EZR で行う方法の解説
ポアソン回帰・ポアソン分布とは
ポアソン回帰とは、まれにしか起こらない現象を数えたカウントデータを目的変数にした回帰分析のこと
カウントデータがポアソン分布に従うと仮定している
平均 $ \lambda $ 回起こる事象が、$ X $ 回起こる確率分布がポアソン分布である
そのときに、ある事象が $ k $ 回起こる確率 $ P(X = k) $ は以下のように書ける
$$ \displaystyle P(X = k) = \frac{e^{-\lambda} \lambda^k}{k!} $$
例えば、$ \lambda = 3 $, $ k = 0, 1, 2, \cdots, 10 $ のときのグラフは以下のようになる
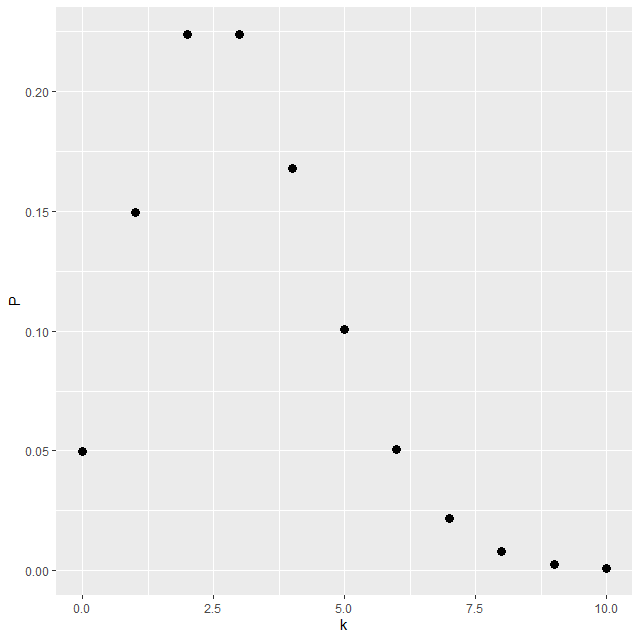
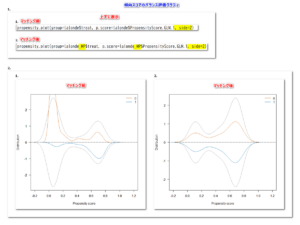
上記グラフの R スクリプトは以下のとおり
### Graph of Poisson Distribution
lambda <- 3
k <- 0:10
P <- exp(-lambda)*lambda^k / factorial(k)
plot(k, P, type='h')
library(ggplot2)
ggplot(data=data.frame(k,P), aes(x=k, y=P))+
geom_point(size=3)
サンプルデータの読み込み
以下のサイトから、data3a.csv をダウンロードする
生態学データ解析 – 本/データ解析のための統計モデリング入門
CSV を読み込むメニューを使って、読み込み
data3a というデータセット名にして、読み込む
カウントデータのアウトカム y と、連続データの x、カテゴリカルデータの f の 3 つのデータ含まれることがわかる

f が、chr(文字型)で認識されているので、因子型に変更しておく
すべての文字変数を因子に変換 メニューを使って、変換する
Factor という表記に変わった

カテゴリカルデータは、この因子型でないと、統計解析に使えないので注意
データの図示
グラフと表の散布図メニューを使って、f の群別の散布図を書いてみる
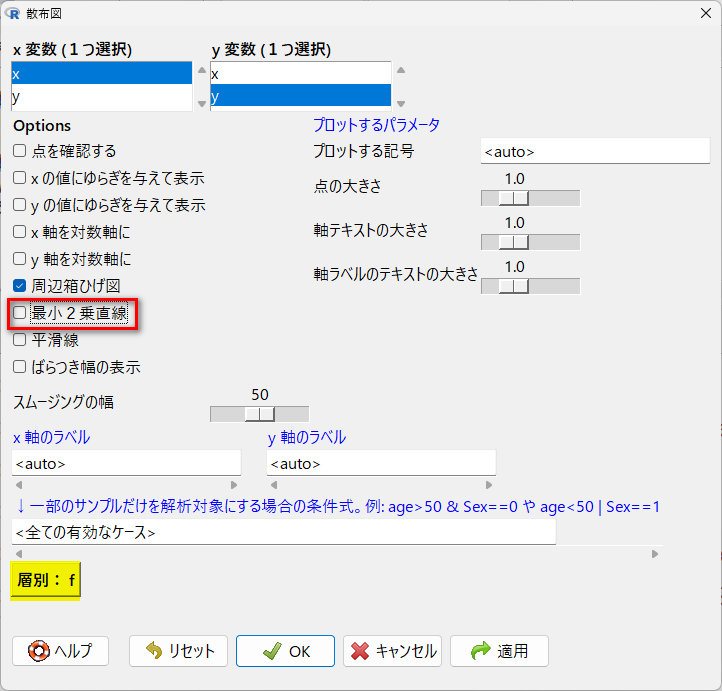
今回は、線形回帰分析ではないので、回帰直線に目を奪われないために、最小 2 乗直線(回帰直線)のオプションは外しておくほうがよい
散布図は以下のとおりだ
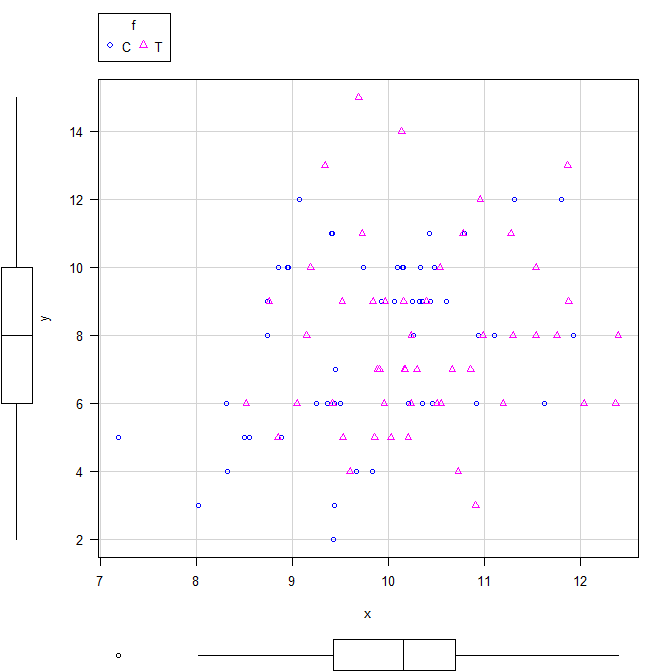
ポアソン回帰のあてはめ(連続データ)
このデータにポアソン回帰をあてはめてみる
まずは、x で y を予測(説明)できるかという計算
標準メニュー → 統計量 → モデルへの適合 → 一般化線型モデル を選択
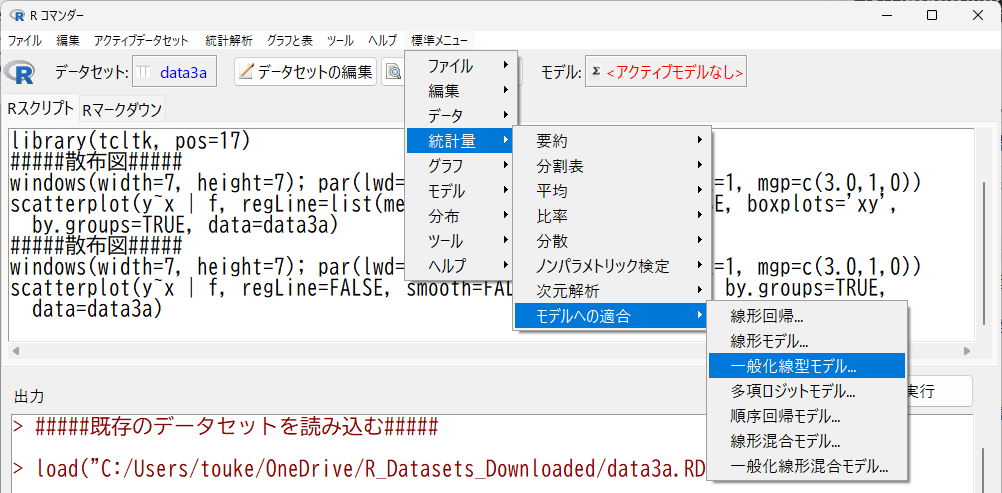
目的変数に y、説明変数に x、リンク関数族は、poisson(ポアソン)をダブルクリックして選択、リンク関数は自動で log が選ばれた状態になるのでそのまま
このように設定する
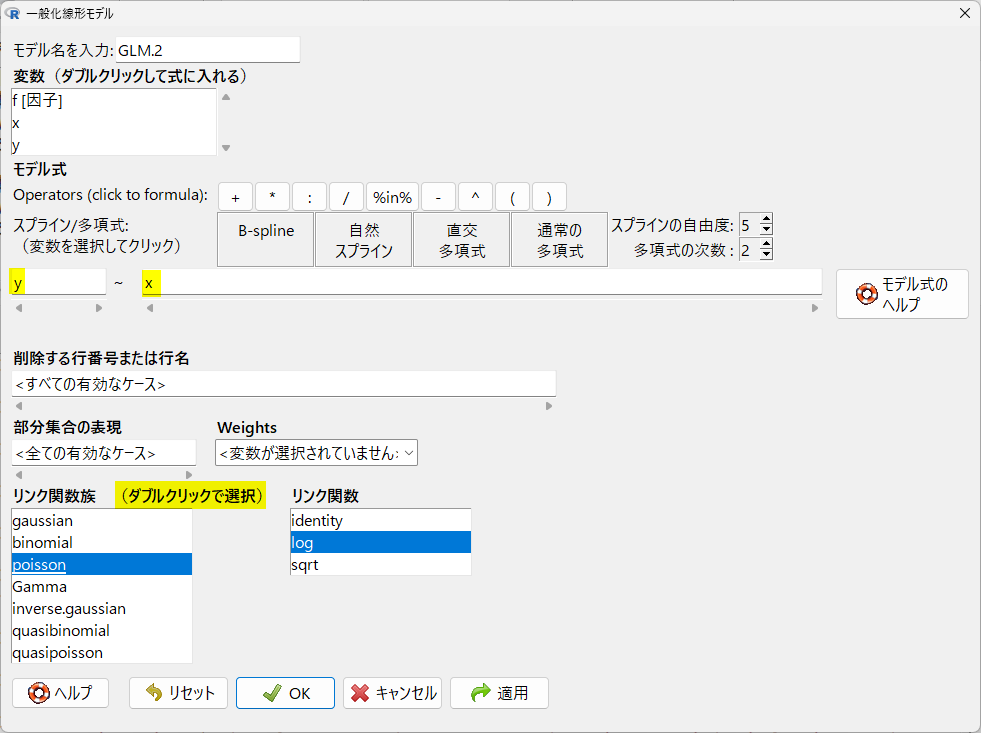
OK をクリックすると計算される
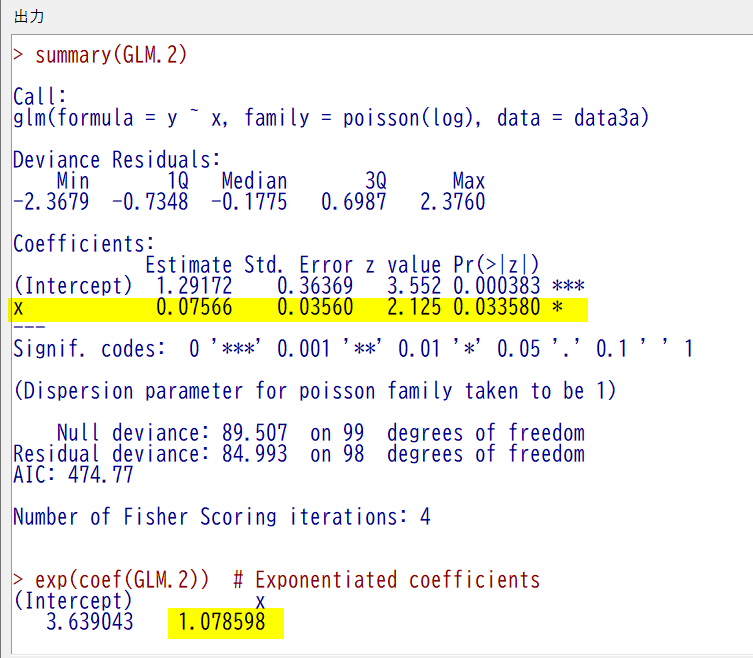
x が 1 上昇するごとに、対数カウントが、0.07566 上昇するという計算結果で、統計学的有意(検定の名前は Wald 検定)
対数カウント上昇を真数カウントに直すと、x が 1 上昇するごとに約 1.08 倍のべき乗($ e^{1.08 x} $)になるという計算になる
ポアソン回帰のあてはめ(カテゴリカルデータ)
変数 f (カテゴリカルデータ)を説明変数にするとどうなるか
メニュー内の設定は以下のとおり
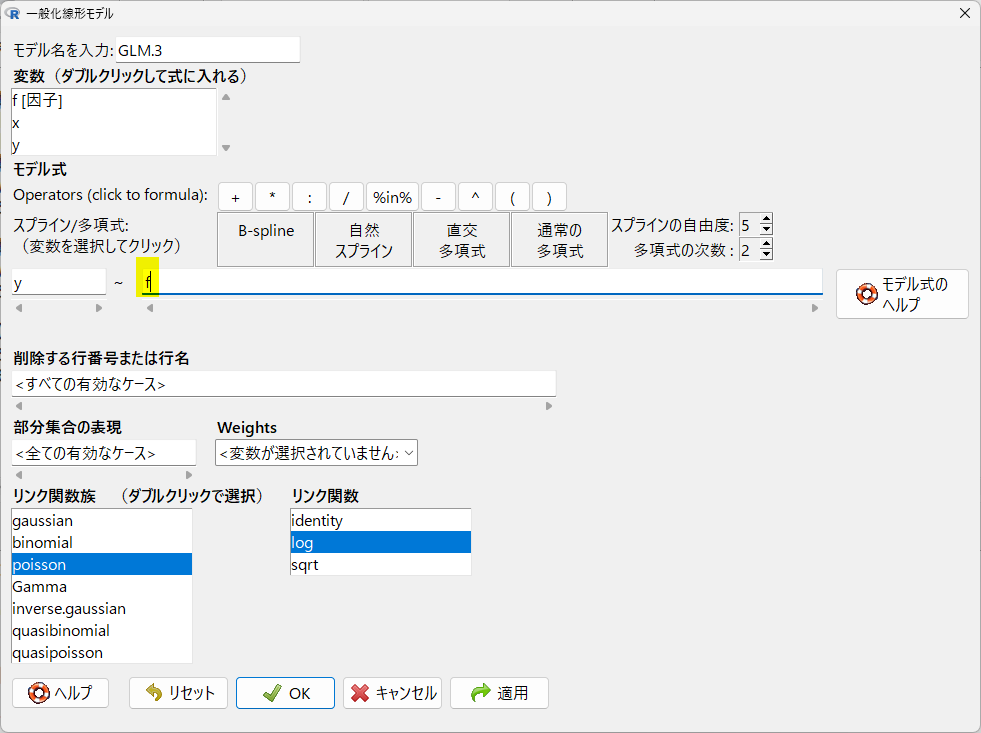
説明変数の部分だけ、x から f に変えた
結果は、以下のとおり
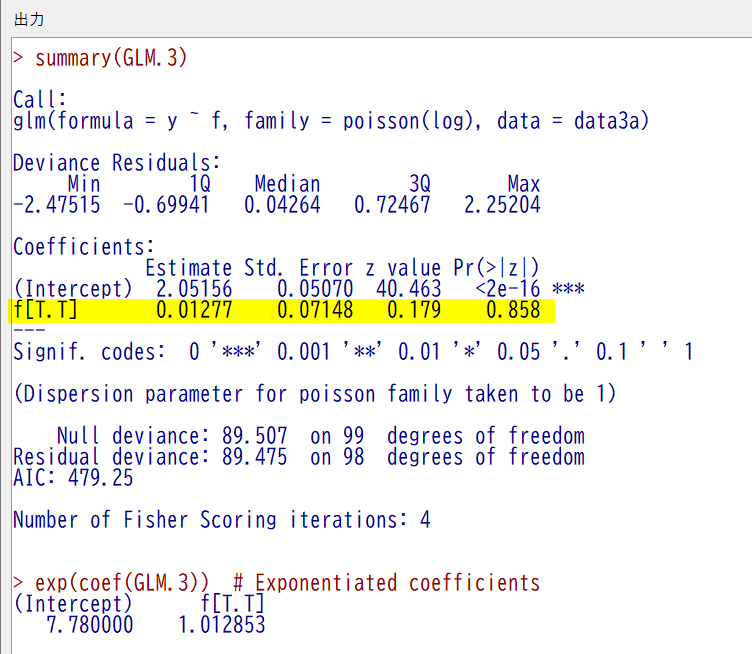
f の C と比較して、T の係数推定値 0.01277 が計算されている
統計学的有意ではない
ポアソン回帰のあてはめ(連続データ+カテゴリカルデータ)
では、変数 x と f をともに説明変数としたらどうだろうか
f の C と T の差を見たいときに、x が交絡因子で、調整しないといけないという状況と考えて計算してみる
ちなみに、C と T では、x の値が異なっており、交絡因子
- y の予後因子、かつ、
- f と関連あり、かつ、
- f と y の中間因子ではない
とみなせる変数である

説明変数の設定は以下のとおり、x と f を + でつなぐ
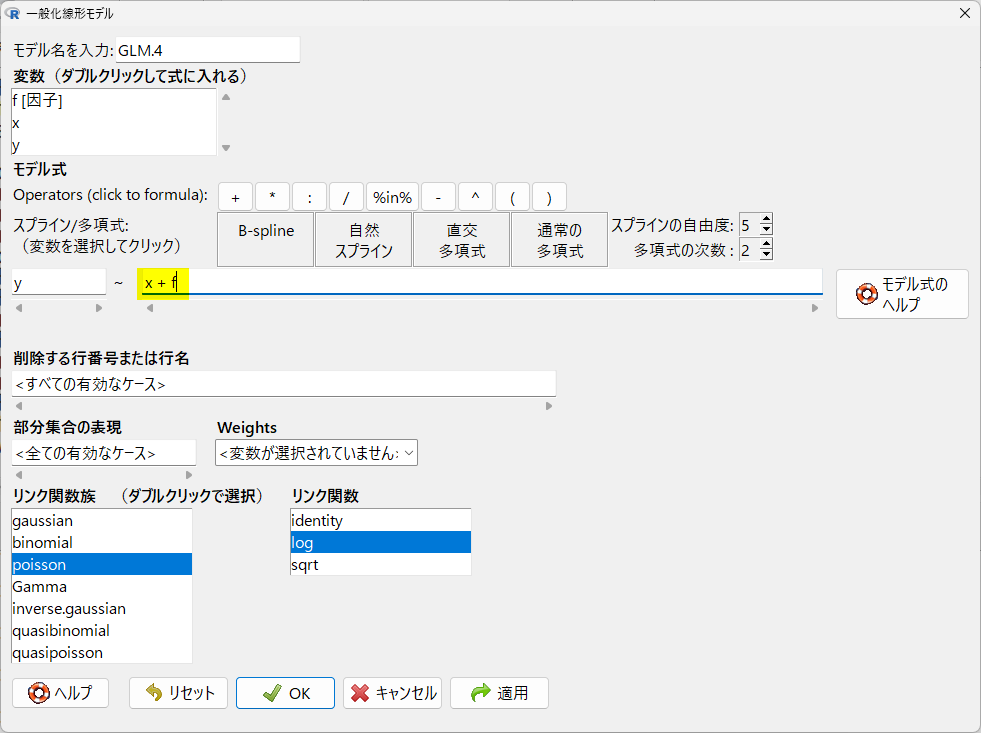
結果は以下のとおり
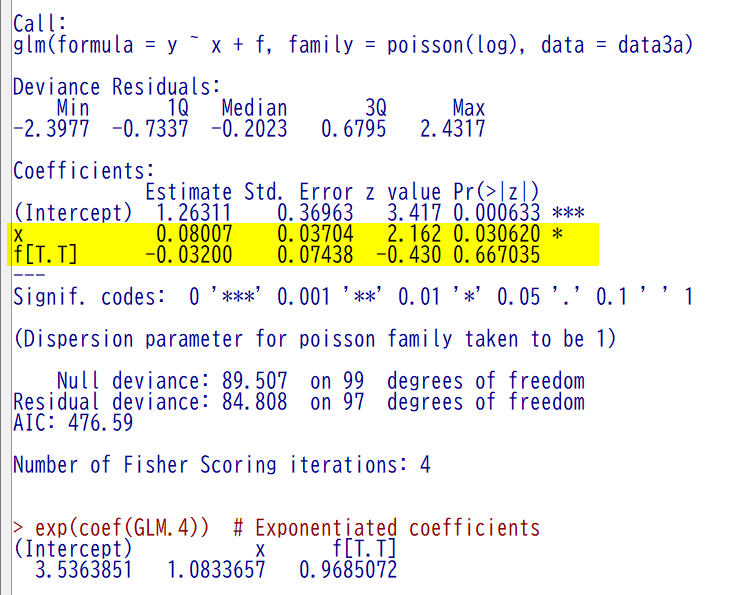
やはり T は統計学的有意ではなかった
なので、C と T の群間差は、明確ではなかったと言える
最初のほうで書いたグラフでも、C と T の差は明瞭ではなかったので、図の印象と符合している
まとめ
ポアソン回帰・ポアソン分布について簡単に解説して、EZR での解析方法を解説した
参考になれば







コメント
コメント一覧 (1件)
[…] EZR でポアソン回帰分析を行う方法 ポアソン回帰を EZR で行う方法の解説 ポアソン回帰・ポアソン分布とは […]