R と EZR で学ぶ主成分分析の計算方法

主成分分析は、多変量情報の縮約と言われるが、実際にはどんな計算をしているのか？

数学的に少し詳しくわかりたい人向け。

主成分分析の計算上の目標は合成変数の作成と分散の最大化

主成分分析の数学的な計算の目的は、合成変数の作成と、その合成変数の分散が最大となるパラメータ（係数）を求めることである。

どんな計算をするのか、一つ一つ順を追って見ていこう。

主成分分析の計算の始まり

主成分分析の計算の始まりは、分散共分散行列もしくは相関行列である。

通常は、単位が違う測定値も同列に扱えるように標準化した値を使った分散共分散行列、つまり相関行列を使った計算を行うため、相関行列での説明に絞ってシンプルに紹介する。

標準化すると、平均がゼロ、分散＝標準偏差＝１となって、計算が楽になるという利点がある。

標準化がいつもの場合も最適かどうかは目的によることを、以下の動画で簡単に触れているので、参考まで。

該当箇所から始まるので注意。

– YouTube

主成分分析の計算を２つの変数での計算で見ていく

２つの変数で作られる合成変数を z とすると、合成変数は以下のように表せる。

\begin{equation}
z = b_1 x_1 + b_2 x_2
\end{equation}

z の分散は以下のように書けるが、z の平均 $ \bar{z} $ は、変数 $ x_1 $, $ x_2 $ とも平均ゼロに標準化されているので、ゼロとなる。

\begin{align}
V_z &= \frac{1}{n} \sum (z – \bar{z})^2 \\
&= \frac{1}{n} \sum z^2 \\
&= \frac{1}{n} \sum (b_1x_1+b_2x_2)^2
\end{align}

式展開して、変数 $ x_1 $, $ x_2$ とも標準化され、分散が１であることから、サンプルサイズ分の和（平方和）を計算すると n になるという性質を利用して、シンプルにしていく。

\begin{equation}
\frac{1}{n} \left( b_1^2 \sum x_1^2 + 2 b_1b_2 \sum x_1x_2 + b_2^2 \sum x_2^2 \right) \\
= b_1^2 + b_2^2 + 2 r_{x_1x_2} b_1b_2
\end{equation}

また、$ x_1 $, $ x_2 $ の積和は、標準化した変数の共分散（でかつ分母は１）の相関係数のサンプルサイズ分の和、つまり相関係数 $ r_{x_1 x_2} $ の n 倍である。

主成分分析の計算の山場　固有値の登場

ここで、係数の２乗和を１とする、制約条件を導入する。

主成分 $ z = b_1 x_1 + b_2 x_2 $ は、$ b_1 : b_2 $ を保っていれば、どのような値をとっても良い状況なのである。

そこで、わかりやすさ重視のため、$ b_1^2 + b_2^2 = 1 $ という制約を加えることにする。

こうすると、主成分の長さ $ \sqrt{b_1^2 + b_2^2} $ が１ということになり、わかりやすい。

標準化をした値を使って、平均ゼロ分散１の変数を使うと、上記で計算がシンプルになったのと同じような理屈である。

最大化したい主成分の分散 $ V_z = b_1^2 + b_2^2 + 2 r_{x_1 x_2} b_1 b_2 $ と、制約条件 $ b_1^2 + b_2^2 = 1 $ がそろったところで、ラグランジュ関数を考える。

ラグランジュ関数は、ラグランジュの未定乗数法を適用した関数である。

ラグランジュの未定乗数法は、制約条件があるときに関数の極値（この場合主成分の分散を最大化する係数）を求める際に、未定の定数をかける方法である。

未定乗数として $ \lambda $ を制約条件にかけて関数に導入する。

この $ \lambda $ が主成分の固有値になる。

\begin{equation}
L (b_1, b_2, \lambda) = b_1 ^2 + b_2 ^2 + 2 r_{x_1x_2} b_1 b_2 – \lambda (b_1 ^2 + b_2 ^2 – 1)
\end{equation}

ここで、$ b_1 $, $ b_2 $, $\lambda$ でそれぞれ偏微分してゼロとおく。

\begin{align}
\frac{\partial L}{\partial b_1} &= 2b_1 + 2r_{x_1x_2} b_2 – 2\lambda b_1 = 0 \\
\frac{\partial L}{\partial b_2} &= 2b_2 + 2r_{x_1x_2} b_1 – 2\lambda b_2 = 0 \\
\frac{\partial L}{\partial \lambda} &= – (b_1 ^2 + b_2 ^2 – 1) = 0
\end{align}

$ b_1 $と$ b_2 $ の偏微分の式は、連立方程式になっていて、

\begin{align}
b_1 + r_{x_1x_2} b_2 &= \lambda b_1 \\
r_{x_1 x_2} b_1 + b_2 &= \lambda b_2
\end{align}

以下のように行列の計算式ととらえることができる。

$$
\begin{pmatrix}
1 & r_{x_1 x_2} \\
r_{x_1 x_2} & 1
\end{pmatrix}
\begin{pmatrix}
b_1 \\
b_2
\end{pmatrix}
=
\lambda
\begin{pmatrix}
b_1 \\
b_2
\end{pmatrix}
$$

ここで、

\begin{pmatrix} b_1 \\ b_2 \end{pmatrix}

が、固有ベクトルである。

両辺に、この固有ベクトルの転置行列を乗ずると、主成分 z の分散が固有値 $ \lambda $ であることが確認できる。

$$
\begin{pmatrix}
b_1 & b_2
\end{pmatrix}
\begin{pmatrix}
1 & r_{x_1 x_2} \\
r_{x_1 x_2} & 1
\end{pmatrix}
\begin{pmatrix}
b_1 \\
b_2
\end{pmatrix}
=
\lambda
\begin{pmatrix}
b_1 & b_2
\end{pmatrix}
\begin{pmatrix}
b_1 \\
b_2
\end{pmatrix}
$$

\begin{align}
b_1 ^2 + b_2 ^2 + 2 r_{x_1x_2} b_1 b_2 &= \lambda (b_1 ^2 + b_2 ^2) \\
V_z &= \lambda
\end{align}

分散（ばらついていること）が情報量と考えると、主成分が持つ情報量は、相関行列の固有値であると言えるわけである。

主成分分析の固有値の求め方

固有値と固有ベクトルの組み合わせは、一つの相関行列から、変数の数だけ計算される。

ここでは計算方法は追わずに、Rであればどのような関数を使えば計算できるか紹介する。

Rの場合

固有値は、Rの eigen() という関数を使うと簡単に計算できる。

固有値は英語で eigenvalue というので、その先頭部分が関数に使われている。

計算方法は、データセットに cor() 関数を適用して、相関行列を計算する。

相関行列に eigen() 関数を適用すれば、固有値と固有ベクトルが計算される。

values が固有値、vectors が固有ベクトルを列方向に並べたものである。

この例では８つの変数を用いているので、８つの固有値と、８列の固有ベクトルが計算されている。

EZRの場合

EZRの標準メニューを使って、標準メニュー→統計量→次元解析→主成分分析を実施すると、以下のような出力になり、Component variancesが固有値、Component loadingsが固有ベクトルと一致していることがわかる。

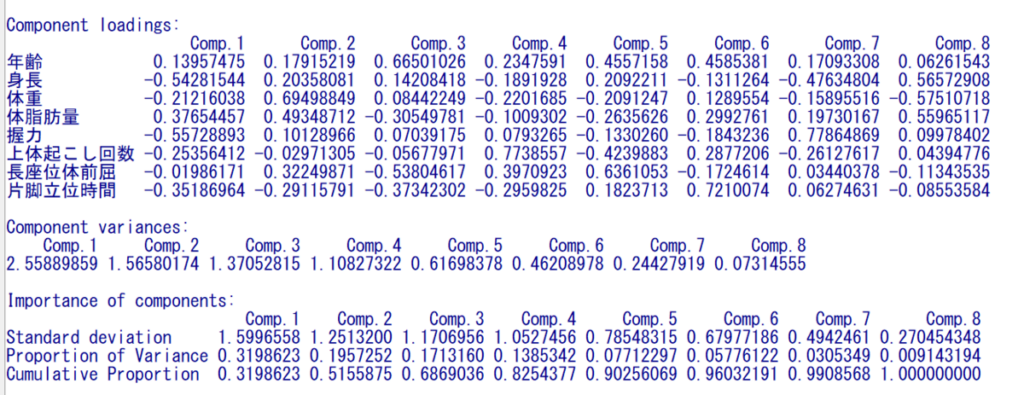
主成分分析の固有値は主成分の重要度の指標

最初に求めた主成分（合成変数 z）が第１主成分、第１主成分に無相関な合成変数が第２主成分となる。

固有値は、第１主成分が最も大きく、だんだん小さくなっていく。

固有値が１以上までの主成分を採用するという慣例がある。

上記の例では、Comp.4までが採用する主成分である。

固有値が大きいほうが、重要な主成分と言える。

主成分分析の寄与率とは？

主成分分析における寄与率とは、ある主成分の固有値を、全主成分の固有値の合計で割った割合である。

第１主成分から次々に足し合わせていった寄与率が累積寄与率である。

第１主成分から足していき、累積寄与率が80%となるまでの主成分を採用するという慣例もある。

上記の例では、Cumulative Proportionとある行で、0.80を超えるComp.4までを採用する主成分とするという意味である。

主成分分析の主成分負荷量とは？

主成分分析における主成分負荷量とは、各変数が持つ各主成分に対する関連の強さを表すものである。

固有ベクトルに固有値の平方根をかけたものである。

下記の例であると、固有ベクトルがL、固有値がlambdaというオブジェクトとすると、aが主成分負荷量である。

左端の赤枠で囲ったところが、第１主成分の主成分負荷量である。

これは第１主成分から計算した合成変数と各変数との相関係数を意味する。

実際に合成変数と各変数の相関係数を計算すると、一致していることがわかる。

右端の赤枠部分である。

この主成分負荷量であると、どの変数が第１主成分と強い関連性があるのかが、相関係数の絶対値判断と同様に理解でき、わかりやすい。

ある変数の主成分負荷量が、絶対値で0.7以上、最低でも0.4以上あれば、その主成分に属すると考える慣例がある。

主成分の意味付けにおいて、ある主成分に強く寄与している変数を見つけることが重要なため、主成分負荷量に意味がある。

固有ベクトルでもある程度関連の度合いはわかるが、主成分負荷量のほうがより鮮明に関連性がわかる指標である。

相関係数と同様に解釈すればよい数値ということで、理解しやすい。

また、主成分負荷量は、標準化していない分散共分散行列から計算を始めた主成分分析で、変数ごとの比較に便利とも説明されるが、上記の通り、標準化した分散共分散行列すなわち相関行列から計算を始めた主成分であっても、主成分における関連性（相関）がわかりやすい点で、主成分負荷量に利がある。

まとめ

主成分分析はどんな計算をしているのか、特に固有値、固有ベクトル、主成分負荷量について、順を追って確認してみた。

主成分分析の理解が進むのに役立ったならば幸い。

参考書籍

SPSSで学ぶ医療系多変量データ解析 第2版

参考サイト

主成分分析と因子分析

https://wiki.cis.iwate-u.ac.jp/~suzuki/biostat/slide/14.pdf

主成分の求め方

16.2 主成分分析結果の解釈

統計学入門−第16章

主成分分析 | 統計科学研究所

https://statistics.co.jp/reference/software_R/statR_9_principal.pdf

固有ベクトル・固有値とは何か？図と具体例から分かるその意味と使い道｜アタリマエ！