主成分回帰と部分的最小二乗回帰を R で実行する方法の解説
部分的最小二乗回帰とは
部分的最小二乗回帰の前に、主成分回帰を説明する。
主成分回帰(Principal Component Regression, PCR)は、主成分分析と回帰分析の融合。
主成分分析で情報の集約をして、変数を減らしてから回帰分析を行う方法。
多重共線性が心配な変数が含まれていても、主成分得点に集約されるため問題がなくなる。
部分的最小二乗回帰(Partial Least Squares Regression, PLS Regression)は、主成分回帰の発展版。
独立変数は主成分回帰と同じ。
PLSは独立変数だけでなく、従属変数にも新たな得点を想定する。
独立変数も従属変数も違う世界に投射して潜在的な関係を見る。
部分的最小二乗回帰の分析例のためにデータとパッケージの準備
データは、ISLRパッケージのCollegeデータを用いる。
米国の777大学の出願者や学生数、書籍購入にかかるコストなどという18個のプロファイルデータ。
解析パッケージはplsパッケージ。
主成分回帰(PCR)も部分最小二乗回帰(PLS)もできる。
最初の一回だけインストールする。
install.packages("ISLR")
install.packages("pls")
使うときはlibrary()で呼び出す。
library(ISLR)
library(pls)
例題は、登録する学生数(Enroll)を予測するモデルを作ること。
まず、説明変数同士の相関係数を見てみる。
Apps(出願者数)とAccept(出願者受付人数)のように0.9を超える相関係数も見られる。
> round(cor(College[,c(-1,-4)]),2)
Apps Accept Top10perc Top25perc F.Undergrad P.Undergrad Outstate Room.Board Books Personal PhD Terminal S.F.Ratio perc.alumni Expend Grad.Rate
Apps 1.00 0.94 0.34 0.35 0.81 0.40 0.05 0.16 0.13 0.18 0.39 0.37 0.10 -0.09 0.26 0.15
Accept 0.94 1.00 0.19 0.25 0.87 0.44 -0.03 0.09 0.11 0.20 0.36 0.34 0.18 -0.16 0.12 0.07
Top10perc 0.34 0.19 1.00 0.89 0.14 -0.11 0.56 0.37 0.12 -0.09 0.53 0.49 -0.38 0.46 0.66 0.49
Top25perc 0.35 0.25 0.89 1.00 0.20 -0.05 0.49 0.33 0.12 -0.08 0.55 0.52 -0.29 0.42 0.53 0.48
F.Undergrad 0.81 0.87 0.14 0.20 1.00 0.57 -0.22 -0.07 0.12 0.32 0.32 0.30 0.28 -0.23 0.02 -0.08
P.Undergrad 0.40 0.44 -0.11 -0.05 0.57 1.00 -0.25 -0.06 0.08 0.32 0.15 0.14 0.23 -0.28 -0.08 -0.26
Outstate 0.05 -0.03 0.56 0.49 -0.22 -0.25 1.00 0.65 0.04 -0.30 0.38 0.41 -0.55 0.57 0.67 0.57
Room.Board 0.16 0.09 0.37 0.33 -0.07 -0.06 0.65 1.00 0.13 -0.20 0.33 0.37 -0.36 0.27 0.50 0.42
Books 0.13 0.11 0.12 0.12 0.12 0.08 0.04 0.13 1.00 0.18 0.03 0.10 -0.03 -0.04 0.11 0.00
Personal 0.18 0.20 -0.09 -0.08 0.32 0.32 -0.30 -0.20 0.18 1.00 -0.01 -0.03 0.14 -0.29 -0.10 -0.27
PhD 0.39 0.36 0.53 0.55 0.32 0.15 0.38 0.33 0.03 -0.01 1.00 0.85 -0.13 0.25 0.43 0.31
Terminal 0.37 0.34 0.49 0.52 0.30 0.14 0.41 0.37 0.10 -0.03 0.85 1.00 -0.16 0.27 0.44 0.29
S.F.Ratio 0.10 0.18 -0.38 -0.29 0.28 0.23 -0.55 -0.36 -0.03 0.14 -0.13 -0.16 1.00 -0.40 -0.58 -0.31
perc.alumni -0.09 -0.16 0.46 0.42 -0.23 -0.28 0.57 0.27 -0.04 -0.29 0.25 0.27 -0.40 1.00 0.42 0.49
Expend 0.26 0.12 0.66 0.53 0.02 -0.08 0.67 0.50 0.11 -0.10 0.43 0.44 -0.58 0.42 1.00 0.39
Grad.Rate 0.15 0.07 0.49 0.48 -0.08 -0.26 0.57 0.42 0.00 -0.27 0.31 0.29 -0.31 0.49 0.39 1.00
Enrollを他のすべての変数で予測する重回帰モデルにあてはめてみて、VIFを計算してみる。
VIFについては以下を参照。

最初の変数 (Privateという変数) を削除して、Enrollを目的変数に、その他の変数を説明変数にして重回帰分析を行い、car パッケージの vif() 関数でVIFを計算させた。
その結果、AppsとAcceptが10を超える数値となり、相関係数0.94を考慮すると、これらが多重共線性を生じていると言える。
> College1 <- College[, -1]
> lm.res1 <- lm(Enroll ~ ., data=College1)
> libarary(car)
> round(vif(lm.res1),1)
Apps Accept Top10perc Top25perc F.Undergrad P.Undergrad Outstate Room.Board Books Personal PhD Terminal S.F.Ratio perc.alumni Expend Grad.Rate
13.5 17.2 7.5 5.6 6.7 1.7 3.9 2.0 1.1 1.3 4.1 4.0 1.9 1.8 3.1 1.8
主成分回帰分析に入る前に、学習データとテストデータに分ける。
5分の4を学習データ、5分の1をテストデータにする。
set.seed(20180924)
sub <- sample(1:777, round(777*4/5))
部分的最小二乗回帰の前に 主成分回帰の分析例
主成分回帰を R で実行してみる。
plsパッケージのpcr()を使う。
クロスバリデーションを行いながらモデルを作るために、validation=”CV”を指定する。
学習データで、モデルを作る。
pcr.res.cv <- pcr(Enroll ~ ., data=College[sub,], validation="CV")
結果のサマリーを確認。
Enrollを除き全部で17変数なので、17の合成変数が作成される。
> summary(pcr.res.cv)
Data: X dimension: 622 17
Y dimension: 622 1
Fit method: svdpc
Number of components considered: 17
VALIDATION: RMSEP
Cross-validated using 10 random segments.
(Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps 8 comps
CV 868.6 791.8 217.1 207.8 207.5 191.5 192.6 192.9 188.5
adjCV 868.6 806.7 216.9 207.6 207.3 191.2 192.2 192.6 188.0
9 comps 10 comps 11 comps 12 comps 13 comps 14 comps 15 comps 16 comps
CV 188.7 188.9 187.9 188.4 186.4 186.5 187.1 187.6
adjCV 188.1 188.3 187.3 187.8 185.8 185.9 186.4 186.9
17 comps
CV 188.0
adjCV 187.3
TRAINING: % variance explained
1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps 8 comps 9 comps
X 47.34 87.44 94.47 96.84 98.42 99.15 99.62 99.97 100.00
Enroll 20.93 93.90 94.39 94.50 95.40 95.43 95.43 95.76 95.76
10 comps 11 comps 12 comps 13 comps 14 comps 15 comps 16 comps 17 comps
X 100.00 100.00 100.00 100.00 100.00 100.00 100.00 100.00
Enroll 95.76 95.81 95.82 95.89 95.89 95.91 95.91 95.91
主成分数ごとのMean Squared Error of Prediction (MSEP)を確認。
plot(MSEP(pcr.res.cv), legendpos="topright")
第二主成分でMSEPは激減してそれ以降は大きくは変わらない。
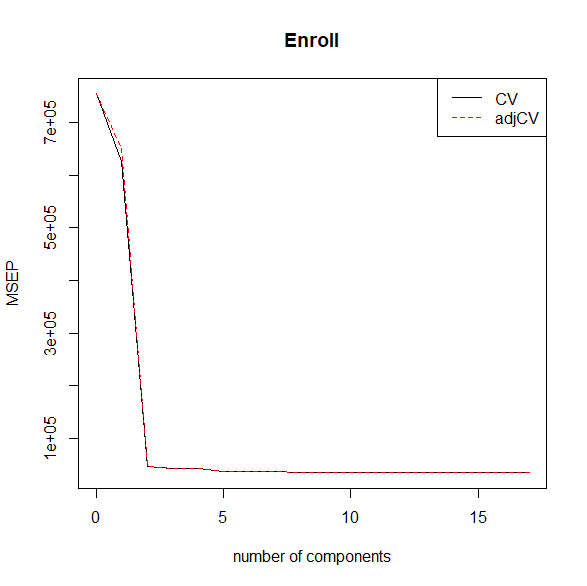
計算上の最適な主成分の数を確認。
答えは5。
selectNcomp(pcr.res.cv, method="onesigma", plot=T)
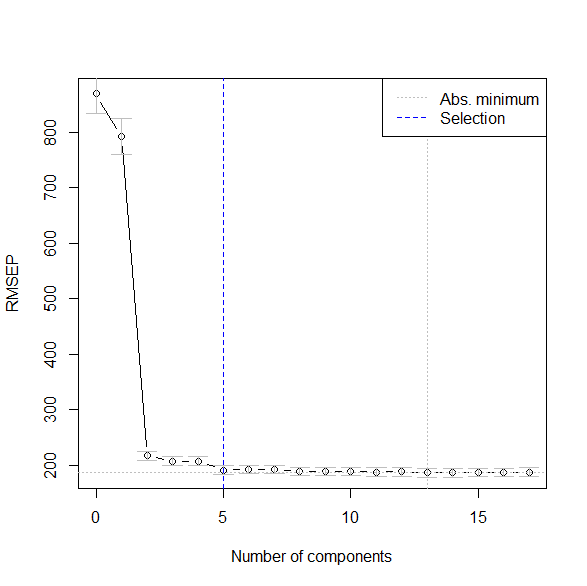
主成分が5の時のMSEPを計算する。
主成分が2の時のMSEPも計算してみる。
MSEP(pcr.res.cv, ncomp=5)
MSEP(pcr.res.cv, ncomp=2)
5のほうがMSEPが小さいことは小さい。
> MSEP(pcr.res.cv, ncomp=5)
(Intercept) 5 comps
CV 754513 36689
adjCV 754513 36571
> MSEP(pcr.res.cv, ncomp=2)
(Intercept) 2 comps
CV 754513 47134
adjCV 754513 47046
テストデータに適用して、MSEPを計算する。
MSEPは学習データに比べてだいぶ大きくなった。
予測性能は高くない。
> MSEP(pcr.res.cv, ncomp=5, newdata=College[-sub,])
(Intercept) 5 comps
1317758 95394
部分的最小二乗回帰の分析例
部分的最小二乗回帰(Partial Least Squares)は、同じ頭文字語になる、Projection to Latent Structureとも呼ばれる。
Projection to Latent Structure(潜在的構造への投射)のほうが、計算方法を反映した名前だ。
使う関数はplsr()で、書き方はpcr()と同じ。
plsr.res.cv <- plsr(Enroll ~ ., data=College[sub,], validation="CV")
summary(plsr.res.cv)
主成分回帰と比較して、第一主成分から Enroll の %Variance が高い。
当てはまりがいいことが期待される。
> summary(plsr.res.cv)
Data: X dimension: 622 17
Y dimension: 622 1
Fit method: kernelpls
Number of components considered: 17
VALIDATION: RMSEP
Cross-validated using 10 random segments.
(Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps 8 comps
CV 868.6 227.6 216.8 203.8 196.6 198.2 195.9 195.0 195.4
adjCV 868.6 227.1 216.3 203.3 195.9 197.2 194.9 194.1 194.5
9 comps 10 comps 11 comps 12 comps 13 comps 14 comps 15 comps 16 comps
CV 195.3 195.1 193.8 194.4 195.1 195.3 195.5 195.6
adjCV 194.4 194.0 192.8 193.4 194.0 194.2 194.4 194.5
17 comps
CV 196.3
adjCV 195.2
TRAINING: % variance explained
1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps 8 comps 9 comps
X 42.16 86.69 93.55 96.13 97.72 98.80 99.49 99.85 100.00
Enroll 93.65 94.32 95.05 95.57 95.68 95.76 95.76 95.76 95.76
10 comps 11 comps 12 comps 13 comps 14 comps 15 comps 16 comps 17 comps
X 100.00 100.00 100.0 100.00 100.00 100.00 100.00 100.00
Enroll 95.87 95.89 95.9 95.91 95.91 95.91 95.91 95.91
第一主成分だけでMSEPはガクンと減少する。
そのあとはなだらかに減少。
plot(MSEP(plsr.res.cv), legendpos="topright")
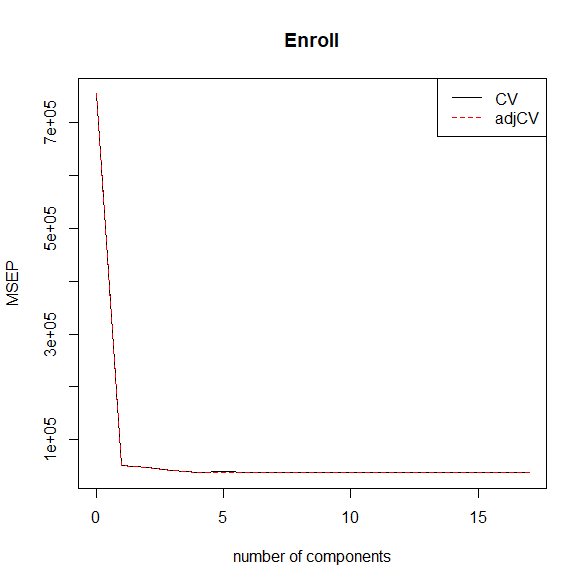
最適な主成分数は4と示された。
selectNcomp(plsr.res.cv, method="onesigma", plot=T)
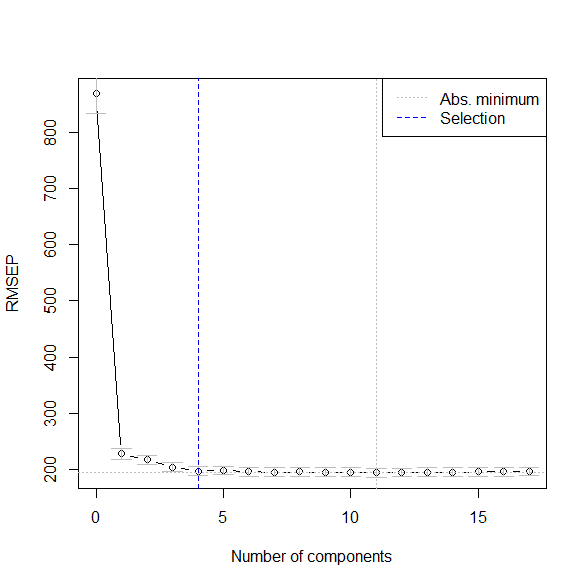
主成分数4のときのMSEPを計算する。
テストデータのMSEPと比較する。
MSEP(plsr.res.cv, ncomp=4)
MSEP(plsr.res.cv, ncomp=4, newdata=College[-sub,])
テストデータのMSEPはぐんと増えてしまって当てはまりはよくなかった。
> MSEP(plsr.res.cv, ncomp=4)
(Intercept) 4 comps
CV 754513 38670
adjCV 754513 38384
> MSEP(plsr.res.cv, ncomp=4, newdata=College[-sub,])
(Intercept) 4 comps
1317758 89507
まとめ
独立変数に多重共線性が疑われるときに有利な主成分回帰と部分的最小二乗回帰。
今回はたまたまテストデータへの当てはまりが悪かっただけと思う。
普通の最小二乗法ならどちらかをやめなければならないような、とても相関が強くて、多重共線性が疑われる変数を同時に扱いたい場合は、どちらの変数もやめなくていい主成分回帰や部分的最小二乗回帰をお試しあれ。







コメント