制限付き 3 次スプライン曲線は、データの非線形関係をとらえるために書いてみるグラフのこと
二値のアウトカムの場合、R でどのように書くか紹介
制限付き 3 次スプライン曲線とは
制限付き 3 次スプライン曲線は、データの非線形関係をとらえるために用いられる曲線グラフのこと
ノット（knots）を設定し、その間で 3 次関数を適用する
ただし、末端部分、つまり、最小値と最大値付近では、線形とするように制限を付けることで、過剰適合（オーバーフィッティング）を防いでいる
ノットの間に 3 次関数を適用することと、末端部分で線形に制限することから、制限付き 3 次スプラインと呼ばれる
他のスプラインとの違いと使い分け
スプラインには、ほかに、B スプライン、罰則付きスプライン（penalized spline）があるが、それらとの違いと使い分けについてまとめてみる
| 制限付き 3 次スプライン | B スプライン | 罰則付きスプライン | |
| 概要 | 両端を線形に制約し、適度に柔軟性を持たせる | 関数の中に局所的な関数（基底関数）を用いたスムージング | B スプラインを使いつつ、過剰適合を抑制する罰則（ペナルティ）を導入 |
| 特徴 | ノット数が少なく、解釈しやすい | 過剰適合を抑えるため、ノット数の調整が必要 | 過剰適合を抑えながらスムーズな曲線が得られる |
| 使い分け | 疫学・医療分野でよく使われる | 高次元データの非線形モデリング | 高次元データの非線形モデリング、時系列データ |
LOESS との違いと使い分け
LOESS (Locally weighted polynomial regression curve)（ロゥエスみたいに発音する）もスプライン曲線に似ている
どちらもデータのスムージング（平滑化）手法の一種で、区間ごとに多項式をフィットさせることで、曲線を作るのは共通
違いをまとめると以下のとおり
| 項目 | スプライン | LOESS |
| アプローチ | グローバル（全体的） | ローカル（局所的） |
| モデル構築方法 | 結節点（ノット knots）を設定し、区間ごとに多項式をつなぐ | 局所的に移動窓を取り、回帰モデルを適用する |
| 関数・滑らかさの制約 | 全体としてスムーズな関数を作るよう制約（e.g., 連続性、微分可能性） | 局所的に回帰を繰り返すので、特定の滑らかさ制約はなし |
| 計算コスト | 比較的低い（行列計算ベース） | 高い（局所回帰を繰り返し計算） |
| おすすめ場面（使い分け） | 全体のトレンドをスムーズに捉えたいとき | 局所的なデータの変動を捉えたいとき |
二値アウトカムの場合 R で制限付き 3 次スプラインを書く方法
二値アウトカムなので、ロジスティック回帰で、制限付き 3 次スプライン曲線を書く
rms パッケージを用いる
まずは、rms パッケージをインストールする
# R コンソールに以下を書いてエンター
install.packages("rms")Japan Yonezawa サーバーからダウンロードしてインストールする
今回サンプルとして使用するのは、EZR の公式マニュアルに付属している Imatinib_Stop というデータセット
イマチニブの中止にかかわる要因の臨床研究データである
EZR の公式マニュアルはこちら → EZRでやさしく学ぶ統計学 改訂3版 〜EBMの実践から臨床研究まで〜
以下のようなスクリプトで、制限付き 3 次スプライン曲線が書ける
# rms パッケージを呼び出す
library(rms)
# データセット名を df とする（これは任意）
df <- Imatinib_Stop
# lrm 関数で計算する； X 軸にしたい連続データに対して、rcs 項を使用する
lrm2 <- lrm(Stop400 ~ rcs(Age) + Sex, data=df)
print(lrm2)
# グラフ描画の準備（rms パッケージを使ってグラフを書く場合のお決り）
ddist <- datadist(df)
options(datadist="ddist")
# グラフを描画する（Y 軸を対数オッズ比にするか、オッズ比にするか、割合にするかは用途による
plot(Predict(lrm2, Age), ylab="log Odds Ratio") # 対数オッズ比
plot(Predict(lrm2, Age, fun=exp), ylab="Odds Ratio" ) # オッズ比
plot(Predict(lrm2, Age, fun=plogis), ylab="Probability") # 割合rms パッケージのロジスティック回帰関数は、lrm 関数である
X 軸にしたい連続データの説明変数に rcs 項を適用する
rcs は Restricted Cubic Spline（制限付き 3 次スプライン）の頭文字である
Y 軸を割合にした場合のグラフを以下に示す
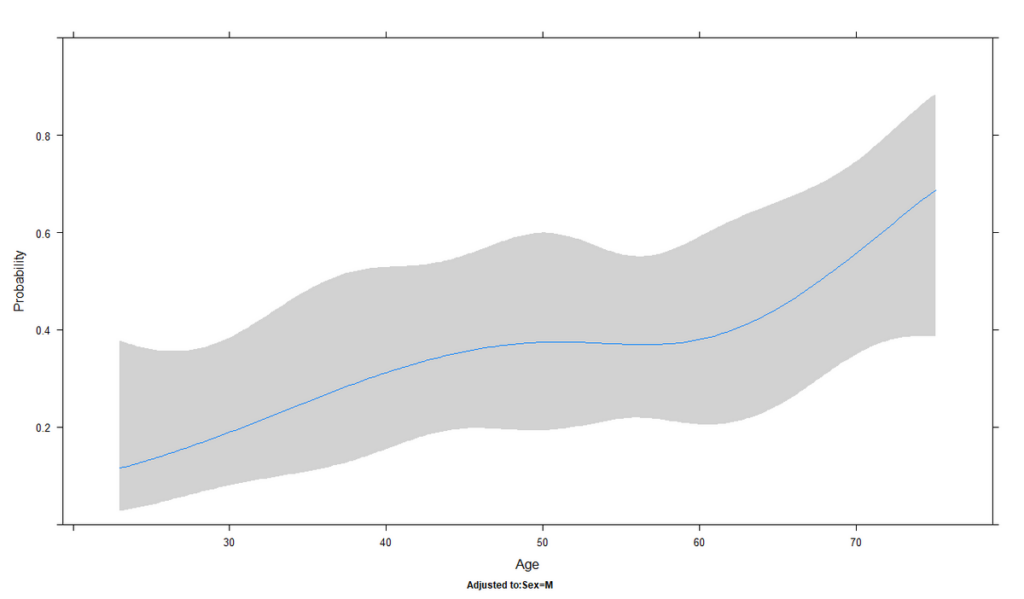
Y 軸が二値アウトカムの推定発生割合、X 軸が年齢とした、制限付き 3 次スプライン曲線である
青線が推定値で、灰色の影が 95 ％ 信頼区間である
別の計算例であるが、Y 軸をオッズ比にした場合の例を以下に挙げる
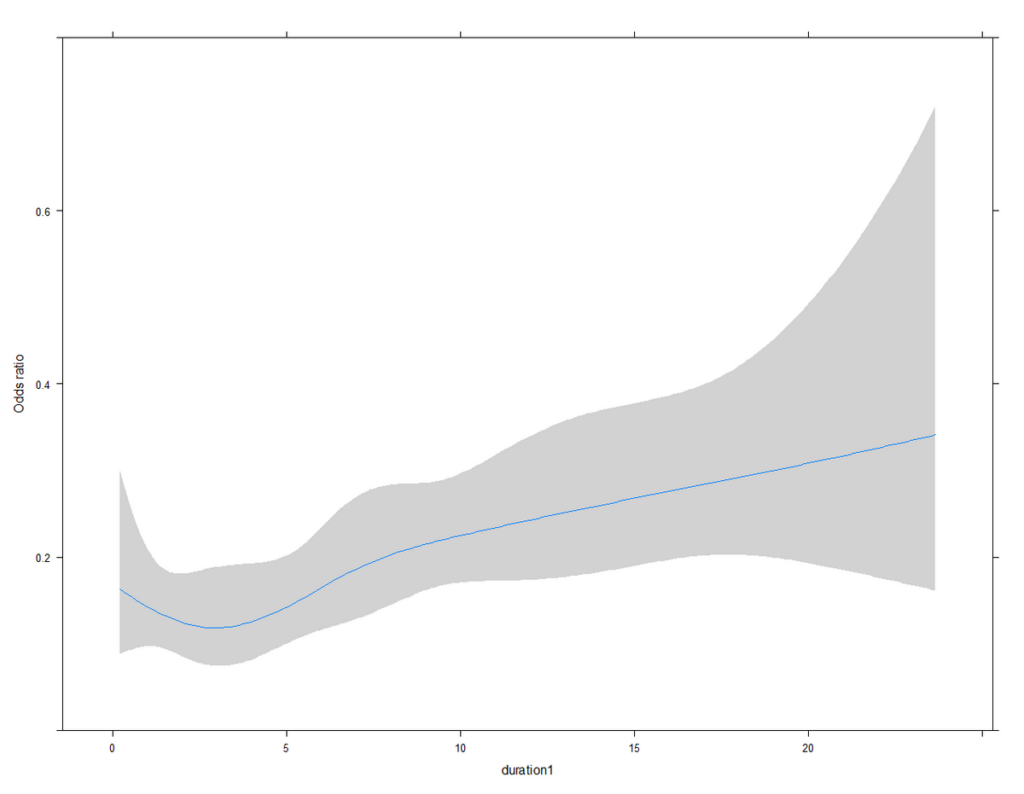
オッズ比の場合、Y 軸を対数表記にしないと、上下の幅が異なって見える
対数オッズ比の場合は、上下の幅が同じになる
割合かオッズ比か
割合のグラフにするかオッズ比のグラフにするかは、目的に応じて異なる
| 項目 | 割合 | オッズ比 |
| メリット | 直感的に理解しやすい | 個人の発生リスクが把握できる |
| デメリット | 個人レベルのリスクを直接的に示せない | 有病割合が高い疾患は過大評価になる |
| おすすめ場面 | 全体の傾向を示す必要がある場合 | 個別リスクを示す必要がある場合 |
| 適用場面 | 公衆衛生、疫学、集団レベル傾向の把握 | 臨床場面、リスク因子の特定 |
まとめ
R で 制限付き 3 次スプライン曲線の書き方について解説した
制限付き 3 次スプラインは、末端部分を線形に制限して、ノット数も抑えて、解釈しやすくしているモデルで、疫学・医療分野で多く使われている
参考になれば
参考記事
BMI, hypertension in Palau, restricted cubic spline method
コメント