カウントデータの散布図に、ポアソン回帰の回帰直線と予測値の 95 % 信頼区間を書き入れたグラフの書き方
ポアソン回帰
まれな事象が起きることを表現したポアソン分布を示すカウントデータ(発生数の数を数えたデータ)を予測する回帰モデル
こちらも参照のこと
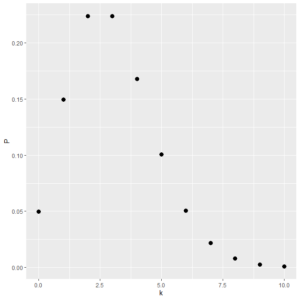
ポアソン回帰のサンプルデータ
サンプルデータは、植物の体サイズ x 、種子数 y のデータである
data3a.csv というデータで、data3a という名前を付けて読み込む
data3a <- read.csv("data3a.csv")
head(data3a)
データセットの先頭部分を示す
今回グループ変数の f は使わない
> head(data3a)
y x f
1 6 8.31 C
2 6 9.44 C
3 6 9.50 C
4 12 9.07 C
5 10 10.16 C
6 4 8.32 C
散布図を見てみる
### Scattergram
library(ggplot2)
ggplot(data=data3a, aes(x=x, y=y))+
geom_point(size=3)+
theme_classic()
散布図は以下のとおり
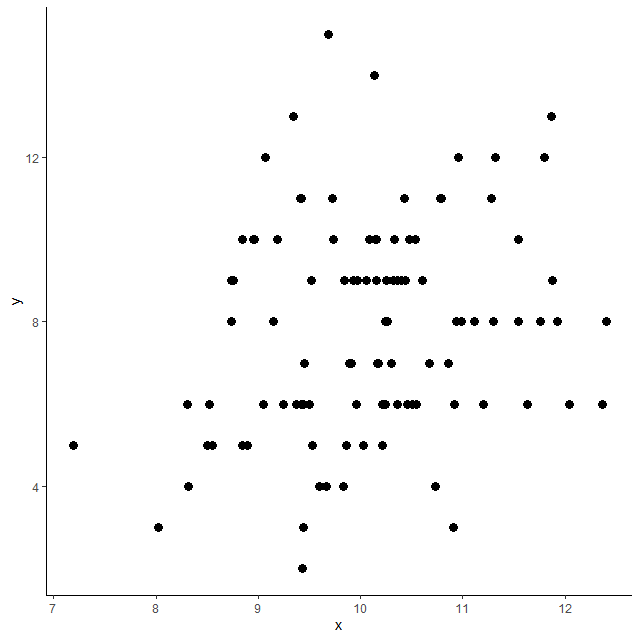
なんとなく右肩上がりの分布のような、そうでもないような・・・
ポアソン回帰:偏回帰係数推定と予測値計算
ポアソン回帰を実際に行ってみる
R では、glm() を使う
family=poisson(link='log')この指定が重要である
スクリプトは以下のとおり
glm.fit1 <- glm(y~x, family=poisson(link='log'), data=data3a)
summary(glm.fit1)
結果は以下のように出力される
> summary(glm.fit1)
Call:
glm(formula = y ~ x, family = poisson(link = "log"), data = data3a)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.3679 -0.7348 -0.1775 0.6987 2.3760
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.29172 0.36369 3.552 0.000383 ***
x 0.07566 0.03560 2.125 0.033580 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 89.507 on 99 degrees of freedom
Residual deviance: 84.993 on 98 degrees of freedom
AIC: 474.77
Number of Fisher Scoring iterations: 4x が 1 大きくなると、y は、0.07566 大きくなる
真数に戻すと個数になる
$ e^{0.07566} = 1.078596 $ なので、約 1 個増えるということだ
予測値の計算
予測式を用いて、予測値の計算を行う
予測式は、$ y = e^{(1.29172 + 0.07566 \times x)} $
予測値は以下のように計算する
予測値を計算するためには、x = new_data を準備しておく必要がある
### Fitted values
new_data <- data.frame(x=seq(min(data3a$x), max(data3a$x),
length=100))
pred.glm.fit1 <- predict(glm.fit1, new_data, type='link',
se.fit=TRUE)
### 95% confidence interval limits
alpha <- 0.05
ci.upper <- exp(pred.glm.fit1$fit +
(qnorm(1-alpha/2)*pred.glm.fit1$se.fit))
ci.lower <- exp(pred.glm.fit1$fit -
(qnorm(1-alpha/2)*pred.glm.fit1$se.fit))ci.upper, ci.lower は予測値の 95 % 信頼区間の上限と下限だ
式で書いてみると以下のようになる
$$ \displaystyle e^{(log(\hat{y}) \pm Z_{\alpha/2} \times SE)} $$
散布図と回帰直線
先ほどの散布図にポアソン回帰で得た回帰直線を書き入れてみる
# 1つ目の散布図
graph1 <- ggplot(data = data3a, aes(x = x, y = y)) +
geom_point(size = 3) +
theme_classic()
# 回帰曲線を重ねる
graph1 +
geom_line(data=data.frame(x=new_data, y=exp(pred.glm.fit1$fit)),
aes(x = x, y = y), linewidth = 2)+
geom_line(data = data.frame(x = new_data, y = ci.upper),
aes(x=x, y=y), linewidth=1, linetype=2)+
geom_line(data=data.frame(x=new_data, y=ci.lower),
aes(x=x, y=y), linewidth=1, linetype=2)
最初の ggplot() で散布図を書き、graph1 + geom_line() で、回帰直線と信頼区間を書き入れる
できあがりの図は以下のとおり
実線が予測値で、破線が信頼区間の上限と下限である
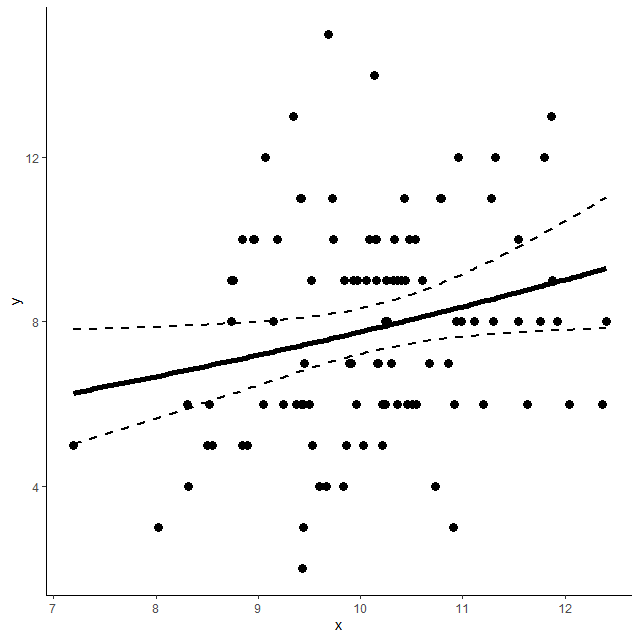
今回のデータを直線で予測するというのはしょせん無理があるなといったところ
まとめ
ポアソン回帰分析から得られた、予測値と 95 % 信頼区間を、元の散布図に書き入れる方法を解説した
参考になれば
参考サイト
ポアソン回帰 | R glm 関数を利用してカウントデータの回帰モデルを作成
参考書籍・サンプルデータ
データ解析のための統計モデリング入門









コメント