反復測定データの解析：EM平均を用いた群間・時点間比較

臨床研究では、同一の対象者に対して複数回測定を行う反復測定デザインが頻繁に用いられる。このようなデータは、時間経過に伴う変化や介入効果を評価する上で非常に有用だが、一方で、複雑な相関構造をモデル化するという課題がある。この複雑な相関構造を適切にモデル化し、群間および時点間での比較を行うために、線形混合モデル (LMM) や一般化線形混合モデル (GLMM) が用いられる。本稿では、これらの混合モデルを用いて解析した反復測定データにおける群間比較および時点間比較を、推定周辺平均 (Estimated Marginal Means: EM平均) を活用して行う方法について解説する。特に、時点間比較における多重比較調整の考え方にも焦点を当て、Rを用いた具体的な計算方法とともに詳述する。

EM 平均を用いた群間比較・時点間比較の概要

EM平均は、モデルによって予測される各要因水準における応答の平均値を推定するものである。共変量の影響を調整した上で、関心のある要因（例えば、群や時点）の効果を純粋に評価できるため、群間や時点間での比較に非常に適している。

• 群間比較: 各時点における群間の差、または全時点を通しての群間の平均的な差を評価する。EM平均を用いることで、他の共変量の影響を調整した上での群間の比較が可能になる。
• 時点間比較: 各群内での時点間の変化、または全群を通しての時点間の平均的な変化を評価する。特に反復測定データでは、治療介入による時間的な効果を評価する上で重要な比較となる。

臨床研究の具体例

ここでは、反復測定データが線形混合モデルや一般化線形混合モデルで解析される具体的な臨床研究例を、データの種類別に紹介してみる。

反復測定連続データ

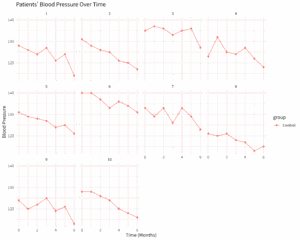
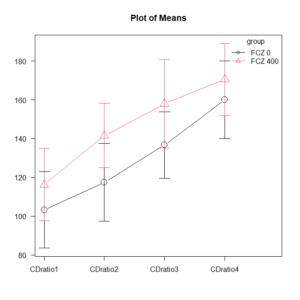
例：高血圧患者における降圧剤の効果
新しい降圧剤Aと既存の降圧剤Bの効果を比較するために、高血圧患者をランダムに2群に割り付け、服薬開始前、1ヶ月後、3ヶ月後、6ヶ月後に収縮期血圧を測定する。目的は、各時点での群間差、および各群内での時間経過による収縮期血圧の変化を評価することである。このデータは連続値であり、正規分布を仮定できるため、線形混合モデルが適用される。

反復測定二項イベントデータ

例：新規抗不安薬の治療反応率
不安症患者を対象に、新規抗不安薬と従来薬の効果を比較する。治療開始後1週間、2週間、4週間、8週間後に、各患者が「治療に反応した（不安症状が50%以上改善）」か「反応しなかった」かを評価する。目的は、各時点における治療反応率の群間差、および各群内での治療反応率の時間的な変化を評価することである。応答変数が二項（反応/非反応）であるため、一般化線形混合モデル (ロジスティック混合モデル) が適用される。

反復測定順序カテゴリデータ

例：変形性膝関節症患者の疼痛症状改善評価
変形性膝関節症患者に対し、標準的な薬剤Aと新しい薬剤Bを比較する。治療開始前（1か月前と比較）、1か月後、2ヶ月後に、疼痛症状の改善の程度を「全く改善なし」「少し改善」「かなり改善」「完全に改善」の4段階で評価する。目的は、各時点での疼痛症状改善評価の群間差、および各群内での疼痛症状改善の時間的な変化を評価することである。応答変数が順序カテゴリであるため、一般化線形混合モデル (順序ロジスティック混合モデル、より具体的には累積ロジット混合モデル) が適用される。

反復測定カウントデータ

例：喘息患者の夜間覚醒回数
喘息患者を対象に、新しい吸入ステロイド薬とプラセボの効果を比較する。治療開始後1ヶ月ごとに、各患者の夜間における喘息による覚醒回数を記録し、1ヶ月後、3ヶ月後、6ヶ月後にその来院前一ヶ月の合計回数を評価する。目的は、各時点での夜間覚醒回数の群間差、および各群内での夜間覚醒回数の時間的な変化を評価することである。応答変数がカウントデータであり、ポアソン分布などを仮定できるため、一般化線形混合モデル (ポアソン混合モデルまたは負の二項混合モデル) が適用される。

Rでの計算方法

Rでの混合モデルの計算には、lme4 パッケージ（LMM, GLMM）、nlme パッケージ（LMM）、emmeans パッケージ（EM平均の計算と多重比較調整）などがよく用いられる。

以下に、架空のデータを用いた各モデルのRコード例を示す。

まず、パッケージの準備。

# 必要なパッケージのインストール (初回のみ)
# install.packages("lme4")
# install.packages("ordinal")
# install.packages("emmeans")
# install.packages("MASS") # 負の二項回帰用
# install.packages("dplyr") # データ操作用

library(lme4)
library(ordinal)
library(emmeans)
library(MASS) # for negative binomial GLMM
library(dplyr) # for data manipulation (optional, but useful)

反復測定連続データ (線形混合モデル)

R 計算例：

# ダミーデータの作成
set.seed(123)
data_lmm <- expand.grid(subject = 1:50, time = c(0, 1, 3, 6))
data_lmm$group <- rep(rep(c("A", "B"), each = 25), times = 4)
data_lmm$blood_pressure <- rnorm(200, mean = 140, sd = 10) # 基準値
data_lmm$blood_pressure[data_lmm$group == "A" & data_lmm$time == 1] <- data_lmm$blood_pressure[data_lmm$group == "A" & data_lmm$time == 1] - 5
data_lmm$blood_pressure[data_lmm$group == "A" & data_lmm$time == 3] <- data_lmm$blood_pressure[data_lmm$group == "A" & data_lmm$time == 3] - 10
data_lmm$blood_pressure[data_lmm$group == "A" & data_lmm$time == 6] <- data_lmm$blood_pressure[data_lmm$group == "A" & data_lmm$time == 6] - 15
data_lmm$blood_pressure[data_lmm$group == "B" & data_lmm$time == 1] <- data_lmm$blood_pressure[data_lmm$group == "B" & data_lmm$time == 1] - 2
data_lmm$blood_pressure[data_lmm$group == "B" & data_lmm$time == 3] <- data_lmm$blood_pressure[data_lmm$group == "B" & data_lmm$time == 3] - 4
data_lmm$blood_pressure[data_lmm$group == "B" & data_lmm$time == 6] <- data_lmm$blood_pressure[data_lmm$group == "B" & data_lmm$time == 6] - 6
data_lmm$blood_pressure <- round(data_lmm$blood_pressure)
data_lmm$subject <- as.factor(data_lmm$subject)
data_lmm$time <- as.factor(data_lmm$time)

head(data_lmm)

# 線形混合モデルの構築
# subjectごとの切片とtimeの効果にランダム効果を仮定
model_lmm <- lmer(blood_pressure ~ group * time + (1 | subject), data = data_lmm)


# 例: 線形混合モデル (model_lmm) を使用
# 各時点での群間比較
emmeans_lmm_time_group <- emmeans(model_lmm, ~ group | time)
emmeans_lmm_time_group2 <- emmeans(model_lmm, specs = "group", by = "time") # ~ と | はそれぞれ specs, by で書いても良い
print(emmeans_lmm_time_group)
print(emmeans_lmm_time_group2)

# pair = TRUE で各時点内での群間比較を行う
contrasts_lmm_time_group <- pairs(emmeans_lmm_time_group)
summary(contrasts_lmm_time_group)

# 例: 線形混合モデル (model_lmm) を使用
# 各群内での時点間比較
emmeans_lmm_group_time <- emmeans(model_lmm, ~ time | group)
# pair = TRUE で各群内での時点間比較を行う
contrasts_lmm_group_time <- pairs(emmeans_lmm_group_time, adjust = "none", reverse = TRUE) # 多重比較調整を適用
summary(contrasts_lmm_group_time)

実行結果：

> summary(contrasts_lmm_time_group)
time = 0:
 contrast estimate   SE  df t.ratio p.value
 A - B       -1.36 2.66 192  -0.511  0.6101

time = 1:
 contrast estimate   SE  df t.ratio p.value
 A - B       -5.60 2.66 192  -2.103  0.0367

time = 3:
 contrast estimate   SE  df t.ratio p.value
 A - B       -6.32 2.66 192  -2.374  0.0186

time = 6:
 contrast estimate   SE  df t.ratio p.value
 A - B       -5.40 2.66 192  -2.028  0.0439

Degrees-of-freedom method: kenward-roger 

時点ごとに比較した結果である。ベースライン（time = 0）は異なるとは言えないが、その後 time = 1, 3, 6 では 5 から 6 程度の差で、有意に異なっている。

> summary(contrasts_lmm_group_time)
group = A:
 contrast      estimate   SE  df t.ratio p.value
 time1 - time0    -4.48 2.66 144  -1.683  0.0946
 time3 - time0   -12.44 2.66 144  -4.672  <.0001
 time3 - time1    -7.96 2.66 144  -2.990  0.0033
 time6 - time0   -12.48 2.66 144  -4.687  <.0001
 time6 - time1    -8.00 2.66 144  -3.005  0.0031
 time6 - time3    -0.04 2.66 144  -0.015  0.9880

group = B:
 contrast      estimate   SE  df t.ratio p.value
 time1 - time0    -0.24 2.66 144  -0.090  0.9283
 time3 - time0    -7.48 2.66 144  -2.809  0.0057
 time3 - time1    -7.24 2.66 144  -2.719  0.0073
 time6 - time0    -8.44 2.66 144  -3.170  0.0019
 time6 - time1    -8.20 2.66 144  -3.080  0.0025
 time6 - time3    -0.96 2.66 144  -0.361  0.7190

Degrees-of-freedom method: kenward-roger 

こちらは、群別の時点間比較結果である。group A も B も time0 または time1 と time3 または time6 との比較で有意になっていることから、それらの時点間が異なることが示唆されている。estimate から判断して group A のほうが大きな変化であることがうかがえる。

反復測定二項イベントデータ

R 計算例：

# ダミーデータの作成
data_binomial <- expand.grid(subject = 1:50, time = c(1, 2, 4, 8))
data_binomial <- data_binomial[order(data_binomial$subject), ]
data_binomial$group <- rep(c("NewDrug", "Control"), each = 100)
# 治療反応率を group と time に応じて設定
data_binomial$response_prob <- ifelse(data_binomial$group == "NewDrug",
    0.4 + data_binomial$time * 0.05,
    0.2 + data_binomial$time * 0.02
)
set.seed(123)
data_binomial$response <- rbinom(nrow(data_binomial), 1, data_binomial$response_prob)
data_binomial$subject <- as.factor(data_binomial$subject)
data_binomial$time <- as.factor(data_binomial$time)

# ロジスティック混合モデルの構築
model_binomial <- glmer(response ~ group * time + (1 | subject), data = data_binomial, family = binomial(link = "logit"))


# 例: ロジスティック混合モデル (model_binomial) を使用
# 各時点での群間比較 (オッズ比で表示)
emmeans_binomial_time_group <- emmeans(model_binomial, ~ group | time, type = "response") # type="response" で確率スケールに変換
contrasts_binomial_time_group <- pairs(emmeans_binomial_time_group, reverse=TRUE)
summary(contrasts_binomial_time_group)

# 例: ロジスティック混合モデル (model_binomial) を使用
# 各群内での時点間比較 (オッズ比で表示)
emmeans_binomial_group_time <- emmeans(model_binomial, ~ time | group, type = "response")
contrasts_binomial_group_time <- pairs(emmeans_binomial_group_time, adjust = "bonferroni")
summary(contrasts_binomial_group_time)

実行結果：

> summary(contrasts_binomial_time_group)
time = 1:
 contrast          odds.ratio    SE  df null z.ratio p.value
 NewDrug / Control       4.11  2.60 Inf    1   2.237  0.0253

time = 2:
 contrast          odds.ratio    SE  df null z.ratio p.value
 NewDrug / Control       2.13  1.34 Inf    1   1.200  0.2300

time = 4:
 contrast          odds.ratio    SE  df null z.ratio p.value
 NewDrug / Control       5.60  3.56 Inf    1   2.708  0.0068

time = 8:
 contrast          odds.ratio    SE  df null z.ratio p.value
 NewDrug / Control      16.12 12.40 Inf    1   3.601  0.0003

Tests are performed on the log odds ratio scale 

時点ごとの群間比較で、NewDrug と Control を time = 1, 2, 4, 8 で比較している。その結果、time = 2 以外では、統計学的有意差ありとの結果であった。

> summary(contrasts_binomial_group_time)
group = Control:
 contrast      odds.ratio    SE  df null z.ratio p.value
 time2 / time1      1.000 0.666 Inf    1   0.000  0.9999
 time4 / time1      1.497 0.957 Inf    1   0.632  0.5275
 time4 / time2      1.497 0.957 Inf    1   0.632  0.5274
 time8 / time1      0.429 0.333 Inf    1  -1.090  0.2756
 time8 / time2      0.429 0.333 Inf    1  -1.090  0.2757
 time8 / time4      0.286 0.216 Inf    1  -1.656  0.0976

group = NewDrug:
 contrast      odds.ratio    SE  df null z.ratio p.value
 time2 / time1      0.519 0.301 Inf    1  -1.133  0.2574
 time4 / time1      2.040 1.240 Inf    1   1.176  0.2396
 time4 / time2      3.933 2.420 Inf    1   2.227  0.0260
 time8 / time1      1.682 0.998 Inf    1   0.876  0.3810
 time8 / time2      3.243 1.950 Inf    1   1.956  0.0505
 time8 / time4      0.824 0.513 Inf    1  -0.310  0.7563

Tests are performed on the log odds ratio scale 

こちらは、群ごとの時点間比較の結果である。NewDrug で、time = 4 と time = 2 の比較が有意差ありであった。明らかな部分はそれだけであり、2群の時点間比較に明確な傾向の違いは見られなかった。

反復測定順序カテゴリデータ

R 計算例：

# 例として、架空のデータを生成
set.seed(456)
n_patients <- 60 
n_visits <- 3

patient_id <- rep(1:n_patients, each = n_visits)
treatment <- sample(c("DrugA", "DrugB"), n_patients, replace = TRUE) %>% rep(each = n_visits)
visit <- rep(c("Baseline", "Post_Treatment_1", "Post_Treatment_2"), times = n_patients)

# 患者ごとのランダムな効果（切片）を生成
random_effect_patient <- rnorm(n_patients, mean = 0, sd = 1.2) %>% rep(each = n_visits)

# 症状改善度の真の確率的な傾向を設定
linear_predictor <- case_when(
    treatment == "DrugA" & visit == "Baseline" ~ 0.2,
    treatment == "DrugA" & visit == "Post_Treatment_1" ~ 0.8,
    treatment == "DrugA" & visit == "Post_Treatment_2" ~ 1.2,
    treatment == "DrugB" & visit == "Baseline" ~ 0.1,
    treatment == "DrugB" & visit == "Post_Treatment_1" ~ 0.4,
    treatment == "DrugB" & visit == "Post_Treatment_2" ~ 0.7,
    TRUE ~ NA_real_
)

# ランダム効果を線形予測子に加える
linear_predictor_with_re <- linear_predictor + random_effect_patient

# 累積確率から症状改善度を生成
thresholds <- c(-1.5, 0.5, 2.0) 

# 症状カテゴリを割り当てる関数
get_ordinal_category <- function(lp_val, thresholds) {
    prob_cum1 <- plogis(thresholds[1] - lp_val) # P(Y <= 1)
    prob_cum2 <- plogis(thresholds[2] - lp_val) # P(Y <= 2)
    prob_cum3 <- plogis(thresholds[3] - lp_val) # P(Y <= 3)

    u <- runif(1) # 一様乱数を生成

    if (u < prob_cum1) {
        return(1) # 全く改善なし
    } else if (u < prob_cum2) {
        return(2) # 少し改善
    } else if (u < prob_cum3) {
        return(3) # かなり改善
    } else {
        return(4) # 完全に改善
    }
}

# 各行について症状改善度を生成
symptom_improvement <- mapply(get_ordinal_category, linear_predictor_with_re, MoreArgs = list(thresholds))

# データフレームの作成
df_ordinal_glmm <- data.frame(
    patient_id = factor(patient_id),
    treatment = factor(treatment),
    visit = factor(visit, levels = c("Baseline", "Post_Treatment_1", "Post_Treatment_2")), # 順序を考慮
    symptom_improvement = ordered(symptom_improvement,
        levels = 1:4
    )
)

# データの確認
head(df_ordinal_glmm)
str(df_ordinal_glmm)

# --- clmm モデルの構築 ---
# formula: 応答変数 ~ 固定効果 + (ランダム効果 | グルーピング変数)
# `symptom_improvement` を応答変数に、`treatment` と `visit` の交互作用を固定効果に指定
# `(1 | patient_id)` は、各被験者ごとのランダム切片を意味し、個人内の反復測定による相関を考慮します。
model_clmm <- clmm(symptom_improvement ~ treatment * visit + (1 | patient_id), data = df_ordinal_glmm)

# モデルのサマリー
summary(model_clmm)

# --- EM平均の計算と群間・時点間比較 ---

# 1. 時点別群間比較 (Between-Group Comparisons at Each Time Point)
# 各時点において、"DrugA" と "DrugB" の症状改善度を比較

# EM平均の算出 (疼痛レベルの各カテゴリの確率として表示されます)
# type = "response" でカテゴリ確率を出力
emmeans_clmm_time_group <- emmeans(model_clmm, ~ treatment | visit, type = "response")
print(emmeans_clmm_time_group)

# 各時点での群間比較
# pairs() で比較を指定。adjust で多重比較調整方法を指定。
# 注意: 順序ロジスティック回帰のEMmeansの出力は各カテゴリの累積確率または個々の確率になるため、
# 比較はオッズ比ではなく、線形予測子スケールでの差分、または確率スケールでの差分となることが多いです。
# ここでは確率スケールで、各カテゴリの確率を直接比較します。
# あるいは、線形予測子スケールで比較し、その結果からオッズ比を解釈することも可能です。

# 線形予測子スケールでの群間比較 (オッズ比は解釈が難しいが、効果の方向性はわかる)
# これは、例えば「中等度以上になる累積オッズ」などの比較になるため、注意が必要です。
contrasts_clmm_time_group_linear <- pairs(emmeans(model_clmm, ~ treatment | visit), reverse = TRUE)
summary(contrasts_clmm_time_group_linear)



# 2. 群別時点間比較 (Within-Group Comparisons Across Time Points)
# 各治療群内において、時間経過による疼痛症状改善レベルの変化を比較

# EM平均の算出
emmeans_clmm_group_time <- emmeans(model_clmm, ~ visit | treatment, type = "response")
print(emmeans_clmm_group_time)

# 各群内での時点間比較
contrasts_clmm_group_time_linear <- pairs(emmeans(model_clmm, ~ visit | treatment), reverse = TRUE, adjust = "none")
summary(contrasts_clmm_group_time_linear)

実行結果：

> summary(contrasts_clmm_time_group_linear)
visit = Baseline:
 contrast      estimate    SE  df z.ratio p.value
 DrugB - DrugA   -0.238 0.508 Inf  -0.468  0.6401

visit = Post_Treatment_1:
 contrast      estimate    SE  df z.ratio p.value
 DrugB - DrugA    0.313 0.512 Inf   0.612  0.5407

visit = Post_Treatment_2:
 contrast      estimate    SE  df z.ratio p.value
 DrugB - DrugA   -0.141 0.519 Inf  -0.272  0.7858

時点ごとの Drug B と Drug Aの差で、いずれの時点も有意差なしであった。

> summary(contrasts_clmm_group_time_linear)
treatment = DrugA:
 contrast                            estimate    SE  df z.ratio p.value
 Post_Treatment_1 - Baseline            0.132 0.476 Inf   0.278  0.7813
 Post_Treatment_2 - Baseline            0.350 0.486 Inf   0.719  0.4720
 Post_Treatment_2 - Post_Treatment_1    0.218 0.476 Inf   0.457  0.6476

treatment = DrugB:
 contrast                            estimate    SE  df z.ratio p.value
 Post_Treatment_1 - Baseline            0.683 0.473 Inf   1.444  0.1486
 Post_Treatment_2 - Baseline            0.446 0.471 Inf   0.948  0.3432
 Post_Treatment_2 - Post_Treatment_1   -0.236 0.483 Inf  -0.490  0.6245

Drugの群ごとの時点間比較で、どちらの群もどの時点間も有意差なしであった。

反復測定カウントデータ

R 計算例：

# ダミーデータの作成
set.seed(123)
data_count <- expand.grid(subject = 1:50, time = c(1, 3, 6))
data_count <- data_count[order(data_count$subject), ]
data_count$group <- rep(c("NewDrug", "Control"), each = 75)
data_count$time <- as.numeric(data_count$time)
# 夜間覚醒回数を group と time に応じて設定 (lambda)
data_count$lambda <- ifelse(data_count$group == "NewDrug",
    3 - data_count$time * 0.1,
    5 - data_count$time * 0.05
)
data_count$awakening_count <- rpois(nrow(data_count), data_count$lambda)
data_count$subject <- as.factor(data_count$subject)
data_count$time <- as.factor(data_count$time)

# ポアソン混合モデルの構築
model_poisson <- glmer(awakening_count ~ group * time + (1 | subject), data = data_count, family = poisson(link = "log"))

# 過分散がある場合、負の二項混合モデルを使用 (MASS::glm.nb を拡張した glmmTMB などが必要だが、ここでは glmer の例としてポアソンを使用)
# library(glmmTMB)
# model_negbin <- glmmTMB(awakening_count ~ group * time + (1 | subject), data = data_count, family = nbinom2(link = "log"))


# モデルのサマリー
summary(model_poisson)

# --- EM平均の計算と群間・時点間比較 ---

#### 1. 時点別群間比較 (Between-Group Comparisons at Each Time Point)
# 各測定時点において、"NewDrug" と "Control" の平均覚醒回数を比較

# EM平均の算出 (type = "response" で元のカウントスケールに変換)
# デフォルトでは線形予測子スケール (log-odds) で計算されるため、
# 覚醒回数そのものの比較には type="response" を指定します。
emmeans_poisson_time_group <- emmeans(model_poisson, ~ group | time, type = "response")
print(emmeans_poisson_time_group)

# 各時点での群間比較
# pairs() でペアワイズ比較を指定。
# ポアソンモデルなので、比較結果は「比率」または「比率の対数（ログオッズ）」として解釈されます。
# type = "response" で比率として結果が出力されます (Risk Ratio または Rate Ratio)。
contrasts_poisson_time_group <- pairs(emmeans_poisson_time_group, reverse = TRUE)
summary(contrasts_poisson_time_group, infer = TRUE) # infer=TRUEで推定値と信頼区間も表示



#### 2. 群別時点間比較 (Within-Group Comparisons Across Time Points)
# 各治療群内において、時間経過による平均覚醒回数の変化を比較

# EM平均の算出
emmeans_poisson_group_time <- emmeans(model_poisson, ~ time | group, type = "response")
print(emmeans_poisson_group_time)

# 各群内での時点間比較
contrasts_poisson_group_time <- pairs(emmeans_poisson_group_time, adjust = "none", reverse = TRUE)
summary(contrasts_poisson_group_time, infer = TRUE)

実行結果：

> summary(contrasts_poisson_time_group, infer = TRUE) # infer=TRUEで推定値と信頼区間も表示
time = 1:
 contrast          ratio     SE  df asymp.LCL asymp.UCL null z.ratio p.value
 NewDrug / Control 0.594 0.0844 Inf     0.450     0.785    1  -3.667  0.0002

time = 3:
 contrast          ratio     SE  df asymp.LCL asymp.UCL null z.ratio p.value
 NewDrug / Control 0.694 0.1040 Inf     0.517     0.932    1  -2.426  0.0153

time = 6:
 contrast          ratio     SE  df asymp.LCL asymp.UCL null z.ratio p.value
 NewDrug / Control 0.400 0.0669 Inf     0.288     0.555    1  -5.476  <.0001

Confidence level used: 0.95 
Intervals are back-transformed from the log scale 
Tests are performed on the log scale 
> 

まず、時点別群間比較の結果を示す。

time = 1, 3, 6 のいずれにおいても、NewDrug のほうが Control に比べて低い（ratio が 1 未満である）ことがわかり、有意差ありであった。

> summary(contrasts_poisson_group_time, infer = TRUE)
group = Control:
 contrast      ratio    SE  df asymp.LCL asymp.UCL null z.ratio p.value
 time3 / time1 0.812 0.105 Inf     0.630     1.047    1  -1.607  0.1079
 time6 / time1 0.940 0.117 Inf     0.736     1.200    1  -0.498  0.6185
 time6 / time3 1.157 0.152 Inf     0.895     1.497    1   1.113  0.2658

group = NewDrug:
 contrast      ratio    SE  df asymp.LCL asymp.UCL null z.ratio p.value
 time3 / time1 0.949 0.153 Inf     0.692     1.302    1  -0.322  0.7472
 time6 / time1 0.633 0.114 Inf     0.444     0.902    1  -2.531  0.0114
 time6 / time3 0.667 0.122 Inf     0.466     0.953    1  -2.221  0.0264

Confidence level used: 0.95 
Intervals are back-transformed from the log scale 
Tests are performed on the log scale 
> 

群別の時点比較では、Control 群では時点間に違いがないのに対し、NewDrug 群では、time 6 vs. time 3 及び time 6 vs. time 1 において、有意差ありという結果であった。

反復測定時点間比較における検定の多重性について

反復測定データにおいて、複数の時点間で比較を行う場合（例：基準時点と1ヶ月後、基準時点と3ヶ月後、1ヶ月後と3ヶ月後など）、多重比較の問題が生じる。多重比較とは、多数の統計的検定を同時に行うことで、本来は有意ではない差を誤って「有意である」と判断してしまう（第一種の過誤）確率が増加する現象である。

例えば、有意水準 α=0.05 で1回の検定を行う場合、誤って第一種の過誤を犯す確率は5%である。しかし、これが10回の検定になると、少なくとも1回第一種の過誤を犯す確率は 1−(1−0.05)10≈0.40 (約40%) にまで上昇してしまう。

したがって、反復測定における時点間比較では、検定の多重性によって、この第一種の過誤の確率のインフレーションが起きることを認識する必要がある。

多重比較調整の方法

多重比較調整の目的は、ファミリーワイズエラー率 (Family-Wise Error Rate: FWER) または偽発見率 (False Discovery Rate: FDR) を制御することにある。

• FWER制御: 少なくとも1つの第一種の過誤を犯す確率を α 以下に抑えることを目指す。より厳密な方法であり、ボンフェローニ補正 (Bonferroni correction) やホルム補正 (Holm correction) などがある。
  • ボンフェローニ補正: 各検定の有意水準を k （比較の総数）で割る（αadjusted​=α/k）。最も保守的な方法であり、検出力が低下しやすいという欠点がある。
  • ホルム補正: ボンフェローニ補正よりも検出力が高く、広く推奨されている。P値を小さい順に並べ、順次調整を行う。
• FDR制御: 誤って棄却された帰無仮説のうち、実際に正しい帰無仮説の割合を制御する。ベンジャミニ・ホックバーグ法 (Benjamini-Hochberg procedure) などがある。探索的な研究や、多くの比較を行う場合に適しており、FWER制御よりも検出力が高くなる傾向がある。

どの調整方法を選択するかは、研究の目的、検定の数、そして第一種の過誤と第二種の過誤のどちらをより重視するかによって決定される。臨床研究では、慎重な結論が求められるため、ボンフェローニ補正やホルム補正がよく用いられる。emmeans パッケージでは、adjust 引数で様々な調整方法を指定できる（例: "bonferroni", "holm", "fdr", "tukey" など）。

多重調整に関する注意点

多重調整は、研究の信頼性を高める上で重要な統計的手法である。しかし、その実施には適切なタイミングがある。

多重調整は、研究デザインの段階、特にサンプルサイズを計算する際に考慮すべき事項である。多くの臨床研究では、実際の診療で得られた症例に基づいて探索的に解析が行われるが、その際、サンプルサイズが十分でなく、統計的な検出力が不足している場合が少なくない。

事前に調整方法を規定せずに事後的に多重比較調整を厳密に行っても、その有効性は限定的だ。

したがって、観察研究で探索的な解析を行う場合など、多重調整を実施しない選択をする際には、「観察型研究であり、探索的な解析であるため、多重比較調整は行わなかった」と明確に記載することをおすすめする。これは、研究の透明性を保ち、結果の解釈をより明確にする上で役立つ。

まとめ

線形混合モデルや一般化線形混合モデルは、反復測定データの複雑な構造を適切に考慮し、群間および時点間での効果を評価するための強力なツールだ。EM平均は、これらのモデルから共変量を調整した上での群や時点の平均値を推定し、比較を行うのに非常に有用である。emmeans パッケージを活用することで、これらの複雑な分析をR上で簡潔かつ正確に実行することができる。本稿で述べた考え方とRコード例が、反復測定データの解析における理解と実践の一助となれば幸いである。