回帰分析におけるロバスト推定法：外れ値に強いモデルを構築する

回帰分析は、変数間の関係性を明らかにする強力な統計ツールである。しかし、データの中に「外れ値」と呼ばれる特異な値が存在する場合、通常の最小二乗法では分析結果が大きく歪められてしまうことがある。このような問題を解決し、より信頼性の高いモデルを構築するために用いられるのが「ロバスト推定法」である。本記事では、ロバスト推定の概念、必要性、具体的な手法、そしてRでの計算例を通じて、その有用性を解説する。

---

ロバスト推定とは

ロバスト推定（Robust Estimation）とは、データ中に外れ値や誤差の分布が正規分布から逸脱している場合でも、推定結果が大きく影響を受けにくい統計的推定方法の総称である。一般的な回帰分析で用いられる最小二乗法（Ordinary Least Squares; OLS）は、残差の二乗和を最小化することで係数を推定するが、この方法は外れ値に対して非常に敏感である。外れ値は残差を大きくするため、その二乗はさらに大きくなり、モデルが外れ値に強く引きずられてしまう傾向がある。

これに対し、ロバスト推定法は、外れ値の影響を小さくするように設計されている。例えば、残差の絶対値を使用したり、外れ値に小さな重みを与えたりすることで、外れ値が推定結果に与える影響を抑制する。

---

ロバスト推定が必要な場合

ロバスト推定が必要となる主なケースは以下の通りである。

• 外れ値の存在: そのデータセットにおいて非常に稀な観測値という形で外れ値は発生する。これらの外れ値が回帰モデルの推定を歪める可能性が高い場合、ロバスト推定が有効である。
• 誤差の非正規性: 最小二乗法は、誤差項が正規分布に従うという仮定のもとで最も効率的であるとされている。しかし、実際のデータでは誤差が正規分布から逸脱していることが少なくない。このような場合でも、ロバスト推定は比較的安定した結果を提供する。
• モデルの頑健性向上: 推定されたモデルが、未知のデータや将来のデータに対しても安定した予測性能を持つことを重視する場合、外れ値の影響を受けにくいロバスト推定は有効な選択肢となる。

---

ロバスト推定の具体例

ロバスト推定にはいくつかの手法があるが、代表的なものとして以下が挙げられる。

• M推定 (M-estimation): 最小二乗法が残差の二乗和を最小化するのに対し、M推定は残差の何らかの関数$ \rho(\cdot) $を最小化する。この$ \rho(\cdot) $は、外れ値に対して残差が大きくなっても、その影響を抑えるように設計されている。ヒューバー関数（Huber function）やチューキー関数（Tukey’s biweight function）などがよく用いられる。
  • ヒューバー関数: ある閾値を超えると、残差の二乗ではなく絶対値に比例するようになる。これにより、極端な外れ値の影響を抑制する。
  • チューキー関数: ある閾値を超えると、残差の影響を完全に無視するように設計されている。より強力に外れ値の影響を排除できる。
• S推定 (S-estimation): 残差の尺度（例：残差の分散）を最小化する推定法である。M推定よりもさらに高い外れ値耐性を持つことが特徴である。
• MM推定 (MM-estimation): M推定とS推定を組み合わせた方法で、高い外れ値耐性と効率性を両立させる。通常、まずS推定で初期値を求め、その初期値を用いてM推定を行うことで、より効率的な推定を実現する。

記事末に３つの推定法の詳細を提示してあるので、興味があれば参照してほしい。

---

Rでの計算例

Rでは、MASSパッケージのrlm()関数や、robustbaseパッケージのlmrob()関数などを用いてロバスト回帰を行うことができる。ここではMASSパッケージのrlm()関数を用いた例を示す。

R スクリプト例：

# データの生成
set.seed(123)
x <- 1:20
y <- 2 * x + rnorm(20, 0, 2)

# 外れ値を導入
y[c(5, 15)] <- c(50, 1) # 2つの外れ値を意図的に導入

# データフレームにまとめる
data_df <- data.frame(x = x, y = y)

# 最小二乗法による回帰
lm_model <- lm(y ~ x, data = data_df)
summary(lm_model)

# ロバスト回帰（M推定 - Huber loss）
library(MASS)
rlm_model_huber <- rlm(y ~ x, data = data_df, psi = psi.huber)
summary(rlm_model_huber)

# ロバスト回帰（M推定 - Tukey's biweight loss）
rlm_model_tukey <- rlm(y ~ x, data = data_df, psi = psi.bisquare)
summary(rlm_model_tukey)

# 結果の比較プロット
library(ggplot2)
ggplot(data_df, aes(x = x, y = y)) +
  geom_point() +
  geom_abline(aes(intercept = lm_model$coefficients[1], slope = lm_model$coefficients[2], color = "最小二乗法", linetype = "最小二乗法")) +
  geom_abline(aes(intercept = rlm_model_huber$coefficients[1], slope = rlm_model_huber$coefficients[2], color = "Huber", linetype = "Huber")) +
  geom_abline(aes(intercept = rlm_model_tukey$coefficients[1], slope = rlm_model_tukey$coefficients[2], color = "Tukey", linetype = "Tukey")) +
  scale_color_manual(name = "モデル", 
                    values = c("最小二乗法" = "red", "Huber" = "blue", "Tukey" = "darkgreen")) +
  scale_linetype_manual(name = "モデル",
                       values = c("最小二乗法" = "dashed", "Huber" = "solid", "Tukey" = "solid")) +
  labs(title = "回帰モデルの比較", x = "x", y = "y") +
  theme_minimal()
ggsave("robust_estimation_linear_reg.png", width = 8, height = 6)

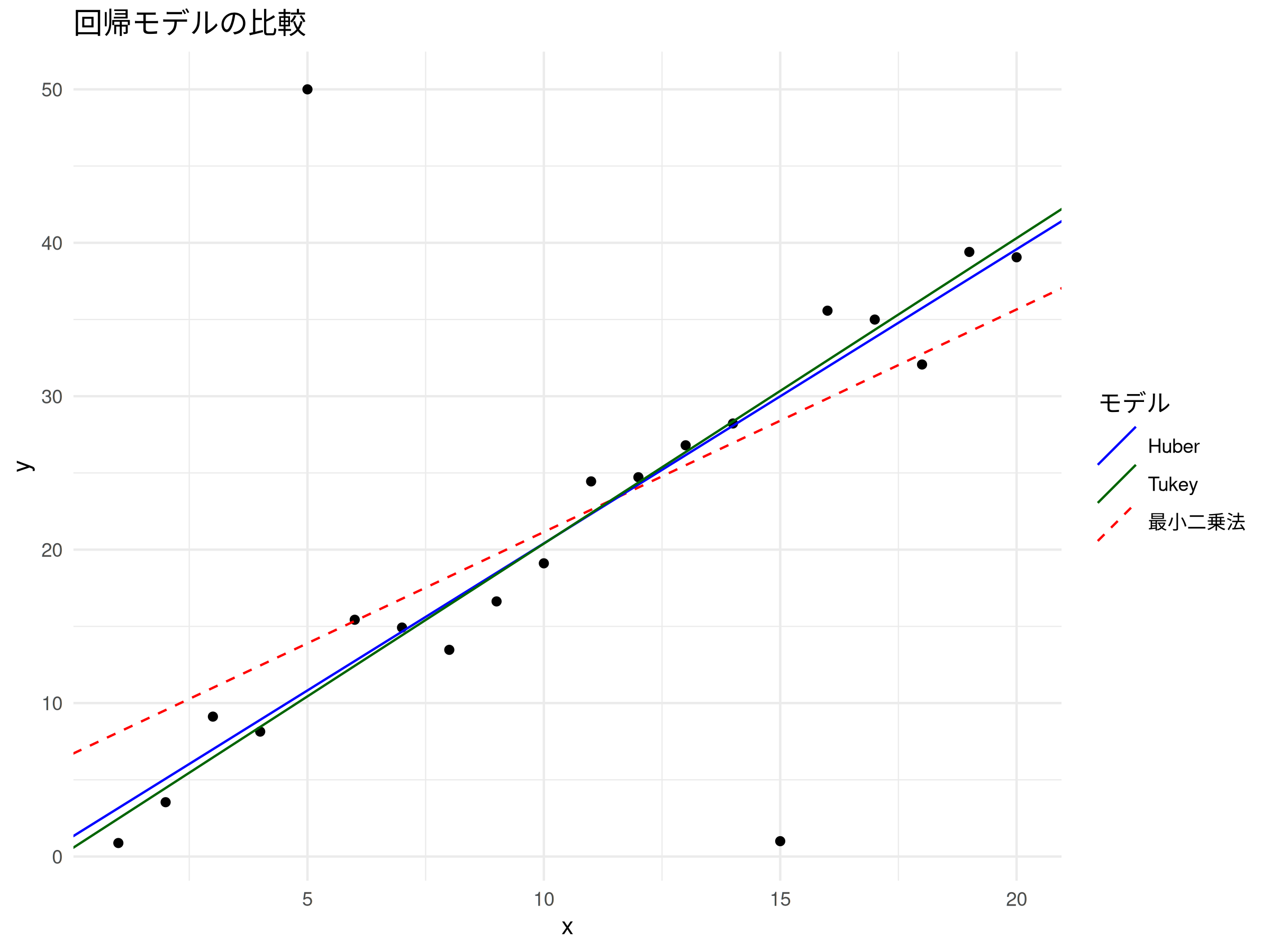
このコードを実行すると、最小二乗法による回帰直線が外れ値に強く引っ張られているのに対し、ロバスト回帰による直線は外れ値の影響を受けにくく、データの本来の傾向に近い形でフィットしていることが視覚的にも確認できる。最小二乗法（赤破線）は、外れ値に影響を受けて、本来の傾きより小さい傾きになっている（下図）

---

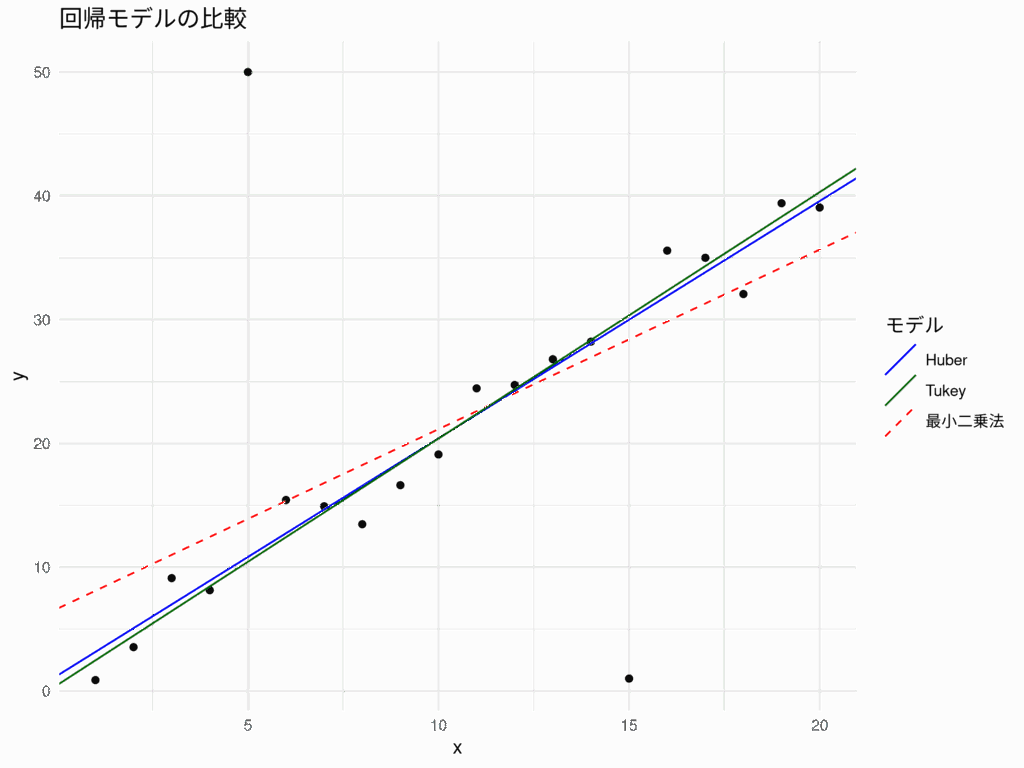
結果解釈例

上記のRコードの出力例を参考に、結果の解釈を行う。

最小二乗法（OLS）の結果

> # 最小二乗法による回帰
> lm_model <- lm(y ~ x, data = data_df)
> summary(lm_model)

Call:
lm(formula = y ~ x, data = data_df)

Residuals:
    Min      1Q  Median      3Q     Max 
-27.403  -3.382  -0.303   2.235  36.102 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)   6.6456     5.2477   1.266  0.22152   
x             1.4505     0.4381   3.311  0.00388 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 11.3 on 18 degrees of freedom
Multiple R-squared:  0.3785,    Adjusted R-squared:  0.344 
F-statistic: 10.96 on 1 and 18 DF,  p-value: 0.003884

> 

外れ値の影響により、切片は高めに、xの係数（真の値は2）は低め（約1.45）に推定されていることがわかる。特に外れ値50の影響が強く出ている。

ロバスト回帰（Huber M推定）の結果

> # ロバスト回帰（M推定 - Huber loss）
> library(MASS)
> rlm_model_huber <- rlm(y ~ x, data = data_df, psi = psi.huber)
> summary(rlm_model_huber)

Call: rlm(formula = y ~ x, data = data_df, psi = psi.huber)
Residuals:
     Min       1Q   Median       3Q      Max 
-28.9935  -1.6168   0.2043   1.8367  39.1758 

Coefficients:
            Value   Std. Error t value
(Intercept)  1.2396  1.3791     0.8989
x            1.9169  0.1151    16.6512

Residual standard error: 2.675 on 18 degrees of freedom
> 

Huber M推定を用いた場合、切片は約1.24、xの係数は約1.92と推定されている。これは、外れ値が導入される前の真の係数（切片0、係数2）に近い値であり、外れ値の影響を効果的に抑制できていることがわかる。

ロバスト回帰（Tukey’s biweight M推定）の結果

> # ロバスト回帰（M推定 - Tukey's biweight loss）
> rlm_model_tukey <- rlm(y ~ x, data = data_df, psi = psi.bisquare)
> summary(rlm_model_tukey)

Call: rlm(formula = y ~ x, data = data_df, psi = psi.bisquare)
Residuals:
     Min       1Q   Median       3Q      Max 
-29.3463  -1.3606   0.1061   1.3358  39.5633 

Coefficients:
            Value   Std. Error t value
(Intercept)  0.4818  1.0859     0.4437
x            1.9910  0.0907    21.9627

Residual standard error: 2.133 on 18 degrees of freedom
> 

Tukey’s biweight M推定を用いた場合も同様に、切片は約0.48、xの係数は約1.99と推定されており、Huber推定よりもさらに真の値に近い結果が得られている。これは、Tukey’s biweightが極端な外れ値に対してより強い影響力抑制効果を持つためと考えられる。

これらの結果から、ロバスト推定法を用いることで、外れ値が存在するデータセットにおいても、より信頼性の高い回帰係数を推定できることがわかる。

---

まとめ

回帰分析において外れ値は常に問題となる可能性がある。通常の最小二乗法では外れ値の影響を強く受けてしまい、分析結果が歪められるリスクがある。ロバスト推定法は、このような外れ値が存在する状況下でも、より安定した信頼性の高い回帰係数を推定するための強力なツールである。

M推定、S推定、MM推定など、様々なロバスト推定法が存在し、それぞれ異なる特性を持つ。データの性質や外れ値のタイプに応じて適切な手法を選択することが重要である。Rなどの統計ソフトウェアを活用することで、これらのロバスト推定法を容易に適用し、外れ値に強い回帰モデルを構築できる。データ分析を行う際には、外れ値の有無を常に意識し、必要に応じてロバスト推定法の導入を検討することで、より正確で頑健な知見を得ることができるだろう。

補足：ロバスト推定の詳細

承知した。回帰分析におけるロバスト推定法、M推定、S推定、MM推定について、それぞれの特徴と仕組みを詳しく解説する。

---

ロバスト推定法（Robust Estimation）とは

ロバスト推定法は、データ中に存在する外れ値（outliers）や、誤差が正規分布に従わない（非正規性）場合に、推定結果がそれらの影響を大きく受けないように設計された統計的推定方法の総称である。

通常の最小二乗法（OLS: Ordinary Least Squares）は、残差の二乗和を最小化することで回帰係数を推定する。しかし、外れ値が存在すると、その大きな残差が二乗されることで非常に大きな値となり、回帰直線が外れ値に強く引きずられてしまう。これは、外れ値がモデルに過度に影響を与え、本来のデータ傾向を正確に捉えられなくなるという問題を引き起こす。

ロバスト推定法は、この外れ値の影響を緩和するために、残差に対する評価方法を工夫する。具体的には、外れ値に対して小さな重みを与えたり、残差が大きくなってもその影響を過剰に評価しないような関数（損失関数または$\rho$関数）を用いることで、より頑健な（ロバストな）推定を可能にする。

---

M推定（M-estimation）

M推定は、ロバスト推定法の基本的な手法の一つで、「最大尤度型推定（Maximum-likelihood type estimation）」の略である。最小二乗法が残差の二乗和を最小化するのに対し、M推定は残差の何らかの関数 $\rho(\cdot)$ の和を最小化する。この $\rho(\cdot)$ 関数は、残差が大きくなるにつれてその影響を抑制するように設計されている。

仕組み:

M推定は、一般的に反復重み付き最小二乗法（IRLS: Iteratively Reweighted Least Squares）を用いて計算される。

• 初期値の設定: まず、通常の最小二乗法などで回帰係数の初期値を推定する。
• 残差の計算: 現在の係数を用いて、各データ点における残差（観測値と予測値の差）を計算する。
• 重みの計算: 各残差に対して、重み関数 $w(\cdot)$ を用いて重みを計算する。この重み関数は、残差が小さいデータ点には大きな重みを、残差が大きい（外れ値の可能性が高い）データ点には小さな重みを与えるように設計されている。
  • $w(e_i) = \frac{\psi(e_i)}{e_i}$ （$e_i$は残差、$\psi(\cdot)$は影響関数で $\rho(\cdot)$ の微分）
• 重み付き最小二乗法の適用: 計算された重みを用いて、重み付き最小二乗法を実行し、新しい回帰係数を推定する。
• 収束判定: 新しい係数が前の反復の係数と十分に近くなった場合（収束基準を満たした場合）は計算を終了する。そうでなければ、手順2（残差の計算）に戻り、残差、重み、係数の計算を繰り返す。

代表的な損失関数（$\rho$関数）と重み関数:

• Huber関数（Huber Loss）:
  • 残差が小さい場合は二乗和と同じように振る舞うが、ある閾値（$k$）を超えると残差の絶対値に比例するようになる。これにより、極端な外れ値の影響を線形に抑制する。
  • $\rho(e) = \begin{cases} \frac{1}{2}e^2 & \text{if } |e| \le k \\ k|e| – \frac{1}{2}k^2 & \text{if } |e| > k \end{cases}$
  • 重み関数は、閾値内では一定、閾値外では残差の絶対値に反比例する。
• Tukey’s Biweight関数（Tukey’s Biweight Loss）:
  • 残差が小さい場合は二乗和のように振る舞うが、ある閾値（$c$）を超えると残差の影響を完全に無視（重みを0）するようになる。これにより、極端な外れ値を強く排除できる。
  • $\rho(e) = \begin{cases} \frac{c^2}{6}\left[1 – \left(1 – \left(\frac{e}{c}\right)^2\right)^3\right] & \text{if } |e| \le c \\\frac{c^2}{6} & \text{if } |e| > c \end{cases}$
  • 重み関数は、閾値外で0となる。

利点:

• 外れ値の影響を効果的に軽減できる。
• 計算が比較的容易。

欠点:

• 「ブレイクダウン点」（データ全体のうち、どのくらいの割合の外れ値まで推定が有効かを示す指標）が低い場合がある（最大で50%）。
• 複数の外れ値が存在する場合に、その検出が難しい場合がある（マスク効果）。

---

S推定（S-estimation）

S推定は、ロバストな尺度（スケール）推定に基づいた推定法である。回帰モデルの残差の尺度を最小化することで係数を推定する。ここでいう尺度とは、残差のばらつきの度合いを示すもので、標準偏差のようなものである。S推定はM推定よりも高いブレイクダウン点を持つことが特徴である。

仕組み:

S推定は、次のように定義される残差の尺度 $\hat{\sigma}$ を最小化する回帰係数 $\hat{\beta}$ を見つけることで行われる。
$$\min_{\hat{\beta}} \hat{\sigma}(\mathbf{e}) \quad \text{s.t.} \quad \frac{1}{n}\sum_{i=1}^n \rho\left(\frac{e_i}{\hat{\sigma}}\right) = K$$
ここで、$e_i$ は残差、$K$ は定数（多くの場合 $E[\rho(Z)]$、ただし $Z$ は標準正規分布に従う確率変数）、$\rho(\cdot)$ は非減少関数で、外れ値に対して影響を抑制するような関数（例：Tukey’s Biweight）が用いられる。

利点:

• 高いブレイクダウン点を持つ（最大50%）。これは、データの半分近くが外れ値であっても、推定が有効であることを意味する。
• 高次元データに対しても比較的安定した性能を示す。

欠点:

• M推定に比べて計算コストが高い。
• 統計的効率がM推定より劣ることがある。

---

MM推定（MM-estimation）

MM推定は、M推定とS推定の利点を組み合わせた手法で、高いブレイクダウン点と高い統計的効率を両立させることを目指す。

仕組み:

MM推定は3つのステップで構成される。

• 初期のS推定: まず、高ブレイクダウン点を持つS推定を用いて、回帰係数のロバストな初期推定値と、残差のロバストな尺度（スケール）を求める。このステップで、外れ値に強い初期値を得ることが目的である。
• M推定: ステップ1で得られたロバストな尺度（スケール）と、ある損失関数（通常はHuber関数など）を用いて、M推定を行う。このステップで、推定の効率性を向上させる。
• 最終的なM推定: ステップ2で得られた係数と、別の損失関数（通常はTukey’s Biweightなど、より強力な影響抑制力を持つもの）を用いて、再びM推定を行う。このステップで、さらに外れ値の影響を排除し、最終的な高効率な推定値を得る。

利点:

• S推定と同様に高いブレイクダウン点を持つ（最大50%）。
• M推定と同様に高い統計的効率を持つ。つまり、外れ値に強く、かつ誤差が正規分布に従う理想的な状況に近い場合でも、通常の最小二乗法に近い性能を発揮する。

欠点:

• M推定やS推定に比べて計算が複雑になる。

---

まとめ

推定法	特徴	ブレイクダウン点	統計的効率
最小二乗法	残差の二乗和を最小化。外れ値に非常に敏感である。	0%	高い（正規分布時）
M推定	残差の特定の関数を最小化。外れ値の影響を軽減する。	低い（約50%）	高い
S推定	残差の尺度を最小化。高いブレイクダウン点を持つ。	高い（50%）	低い
MM推定	S推定で初期値を求め、M推定で効率を高める。高ブレイクダウン点と高効率を両立させる。	高い（50%）	高い

ロバスト推定法は、現実のデータによく見られる外れ値や非正規性といった問題に対処するための強力なツールである。特にMM推定は、高い頑健性と効率性を兼ね備えているため、回帰分析で外れ値が懸念される場合に推奨されることが多い手法である。どの手法を選択するかは、データの性質や分析の目的に応じて慎重に検討する必要がある。