主成分分析で軸の回転をすることはできるか
主成分分析とは?
主成分分析とは、多数の変数の情報を少数の合成変数に縮約する解析手法である。
たくさん変数があると何がどうなっているかわからないが、それら変数同士の相関関係を活用して、代表的な方法としては2つの合成変数に縮約し可視化して、全体像を把握するという手法である。
少し詳しい計算方法は以下を参照。

主成分分析の実例はこちら。
主成分分析の軸の回転とは?
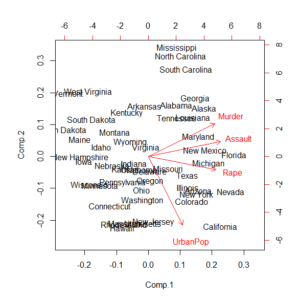
軸の回転とは、2つの主成分の主成分負荷量をプロットした主成分プロットを回転させることである。
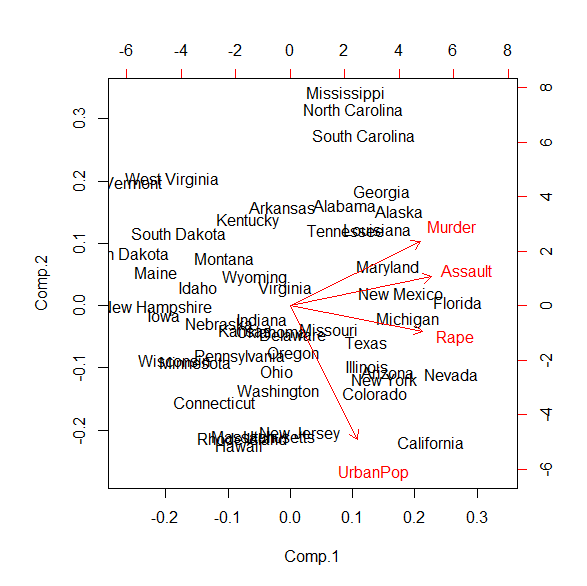
この図が、主成分プロットの例である。
米国の州の名前のプロットは気にせず、赤い文字だけに注目してほしい。
Murder, Assault, Rapeと、UrbanPopの2グループに分かれているように見える。
ただし、UrbanPopは、Comp.2軸に平行ではなく、少しだけずれている。
この時、この図が少しだけ時計回りに回転したら、UrbanPopは、真下に向いてComp.1の0.0を指すに違いない。
そうすると、Comp.2がUrban Populationが多いか少ないかという軸という見方がより強くできるようになる。
Comp.1については、Murder, Assault, Rapeのような犯罪が多いか少ないかという軸として、いまよりもっと明確に解釈できる。
軸の回転にはこういう利点がある。
因子分析はこの回転によって、解釈しやすくするのが一般的だが、主成分分析で行っても差し支えない。
主成分分析で軸の回転 SPSSで行う方法
詳しい計算方法は、下記参考サイト参照。
実際にSPSSでどのように行うかを紹介したい。
サンプルデータはRに組み込まれているUSArrestsという米国の犯罪件数と都市部の人口データを用いる。
まず、SPSSにデータを読み込み、「分析」→「次元分解」→「因子分析」を選択する。
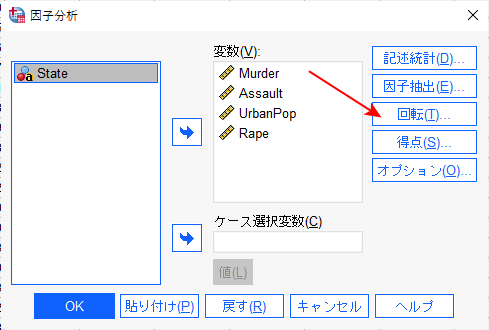
変数を投入する。
因子の抽出をクリックする。
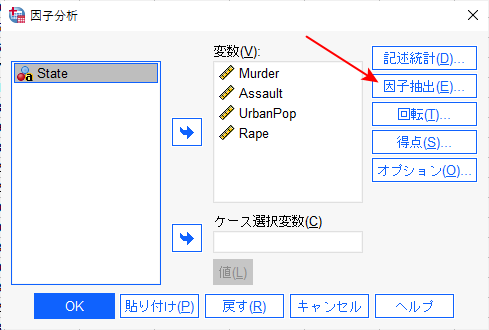
方法が主成分分析であることを確認して、抽出の基準は因子の固定数として、抽出する因子は主成分プロットのためと考えて、今回は2とする。
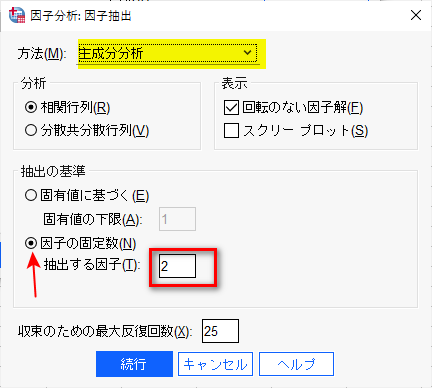
続行をクリックして戻った後、回転をクリックする。
まずは、回転はなしで、因子負荷プロットにチェックを入れる。
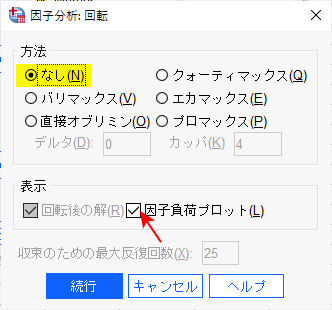
これで、続行をクリックし、OKをクリックすると、計算される。
主成分分析の結果の読み方
説明された分散の合計というタイトルの表が、いわゆる固有値とか寄与率の話である。
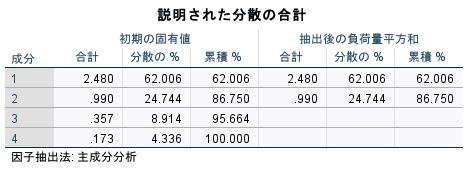
一番左のカラムの合計が、固有値である。これが1を超えている主成分が十分な情報を持った採用すべき主成分となる。
今回は第2主成分の固有値がほんの少し1を下回っているが、ほぼ1とみなして、採用することにする。
第1、第2主成分で、全体の86.75%を説明している。
これを累積寄与率と呼び、80%を超えるところまでの主成分を採用するという慣例もある。
成分行列とのタイトルの表が、主成分負荷量の表である。
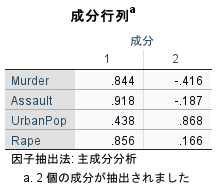
この負荷量の絶対値が大きい変数が、当該主成分に属すると考えればよい。
今回の場合は、Murder, Assault, Rapeが第1主成分、UrbanPopが第2主成分に属すると考えるのが妥当だろう。
最後が、メインの主成分プロットである。
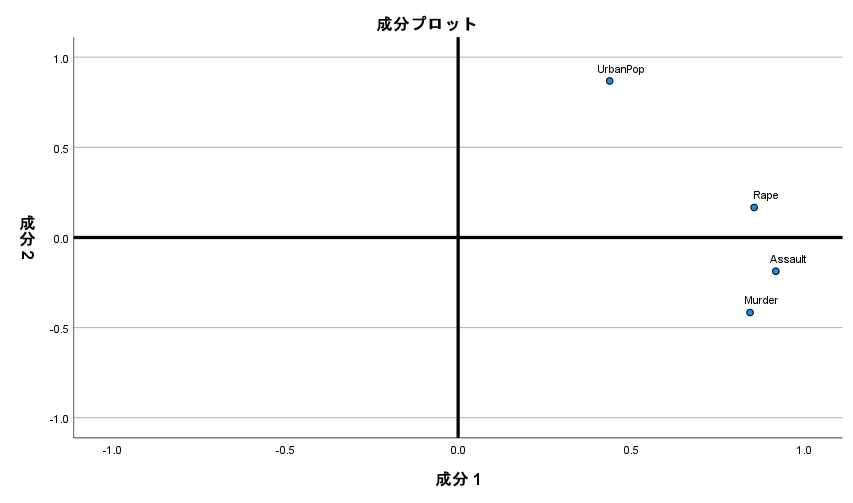
第1主成分が大きいところにMurder, Assault, Rapeがプロットされており、第2主成分が大きいところにUrbanPopがプロットされている。
これが回転前の結果である。
主成分分析 軸の回転方法、回転後の結果とその読み方
軸の回転は、回転オプションで指定する。
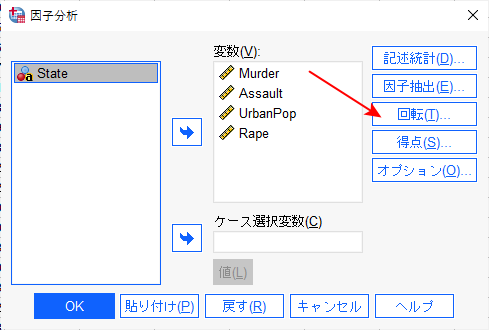
バリマックスをクリックする。
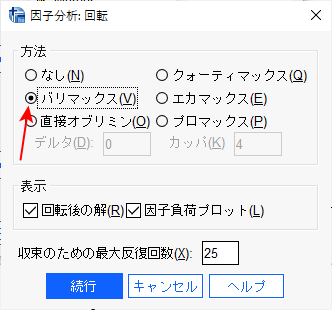
続行とクリックして、OKをクリックすると、計算される。
説明された分散の合計の表に、回転後の固有値の計算結果が追加される。
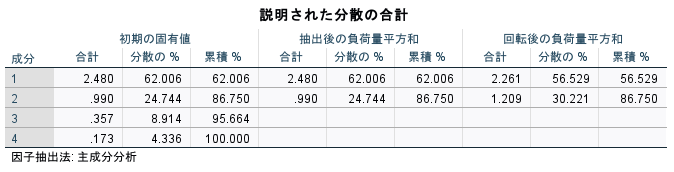
それほど大きな違いはないが、第2主成分の固有値が1を超えて、1.209となった。
回転後の主成分負荷量は、回転後の成分行列というタイトルの表として出力されている。
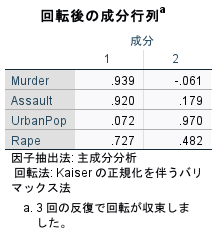
回転前と比べると、第1主成分、第2主成分に属している変数がより際立っているように見える。
回転後の主成分プロットは以下のとおりである。
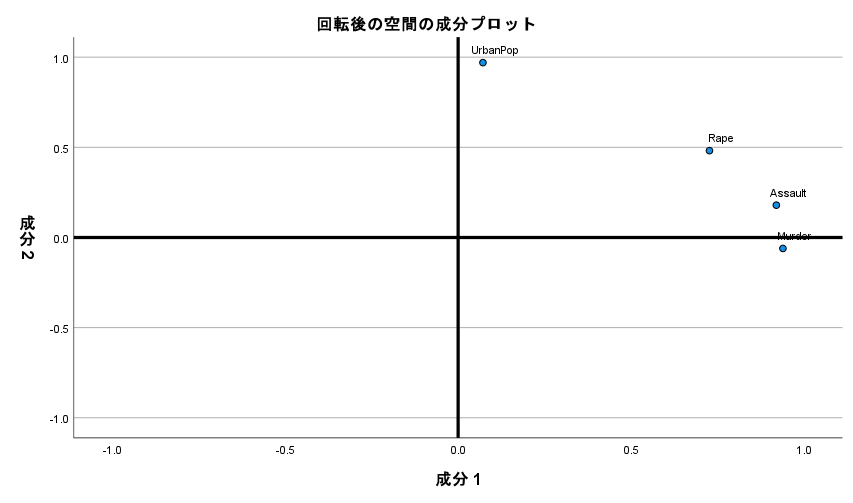
第1主成分と第2主成分がよりはっきりしたと思う。
ちなみに、今回の場合、主成分の抽出個数を、例えば全変数の数4と設定して計算すると、グラフが変わる。
まず三次元で表示される。
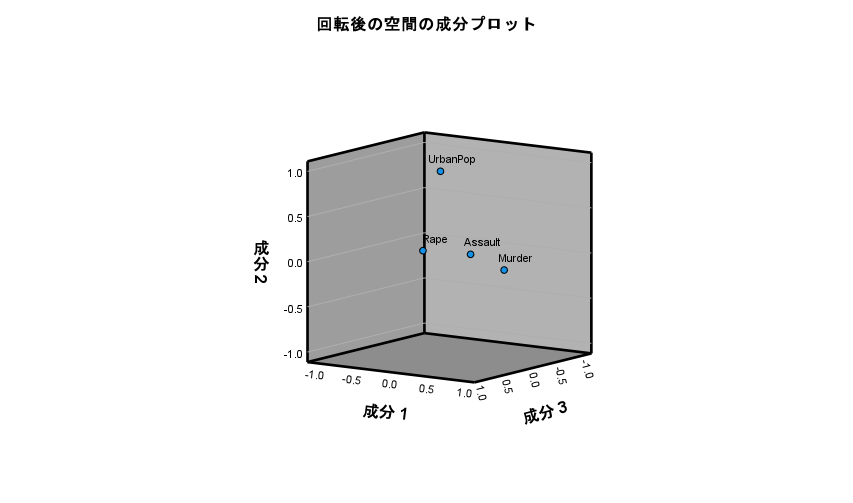
二次元にするために、図をダブルクリックして、さらにZ軸あたりをダブルクリックして、プロパティを表示させたのちに、Z軸を除外する。
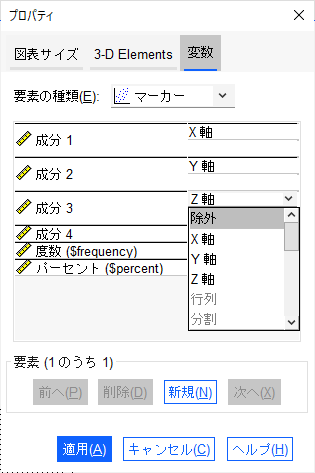
原点の線を追加すると、以下のような二次元主成分プロットになる。
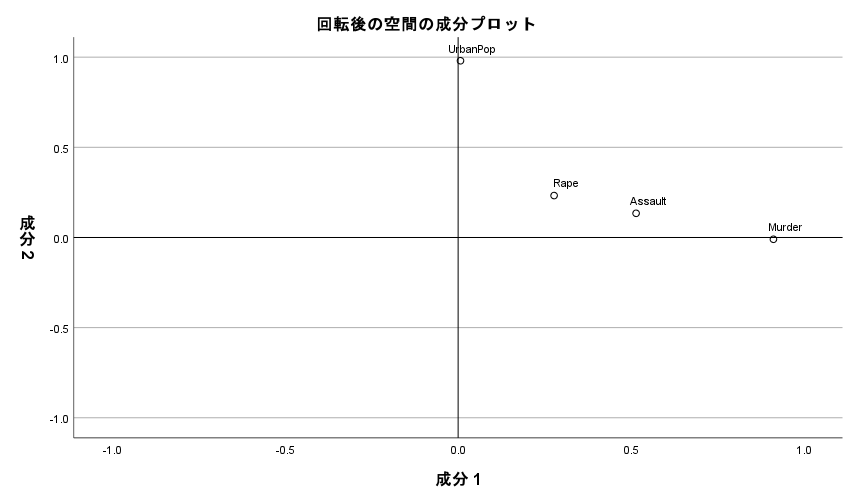
先ほどの主成分プロットと比べると、Rapeがかなり原点に寄っている。
主成分負荷量を見るとその原因がわかる。
実は、Rapeの第3主成分の主成分負荷量が高くなっており、第1、第2主成分で説明できない第3の主成分に属する変数として異なる性質を持っている可能性がある。
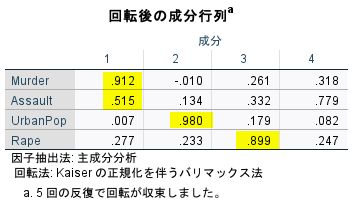
今回は、主成分として採用すべきは第2主成分までと、回転前に見極めていたので、回転は2因子指定の主成分分析として実施して、回転後の主成分プロットを描画するほうが適切であろう。
主成分分析 軸の回転 Rで行う方法
Rの psych パッケージの principal() 関数を使うと、SPSSの計算の再現ができる。
まずは、インストールして、パッケージを呼び出すところまで行う。
install.packages("psych")
library(psych)
USArrests データセットは組み込みデータであるので、このデータセットの名前を書けば直接呼び出せる。
回転前の主成分分析の結果は以下の通り。
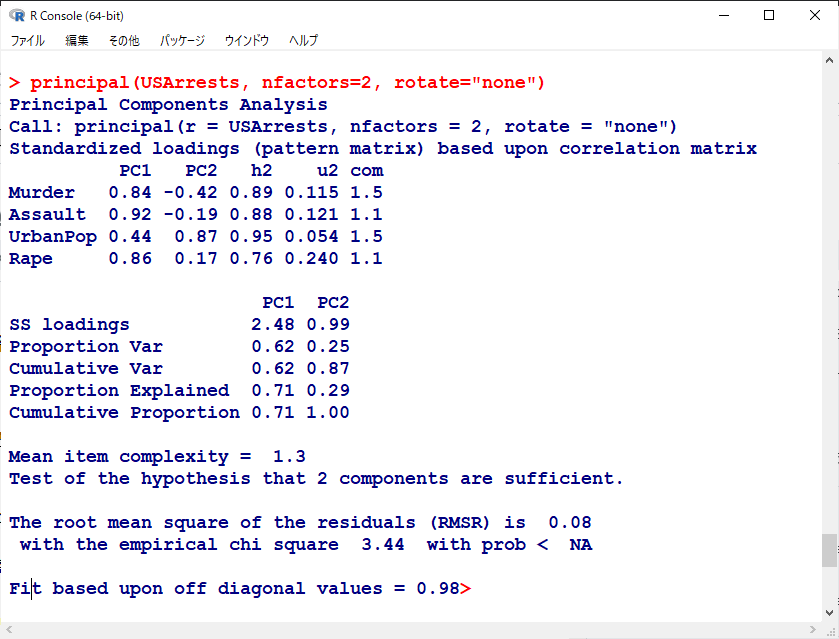
Standardized loadingsとあるセクションのPC1, PC2というのが、回転前の主成分負荷量である。
また、次のセクションのSS loadingsとあるのが、固有値の値である。
Cumulative Varが累積寄与率である。
いずれも上述のSPSSの出力と一致している。
回転後の結果は以下の通り。
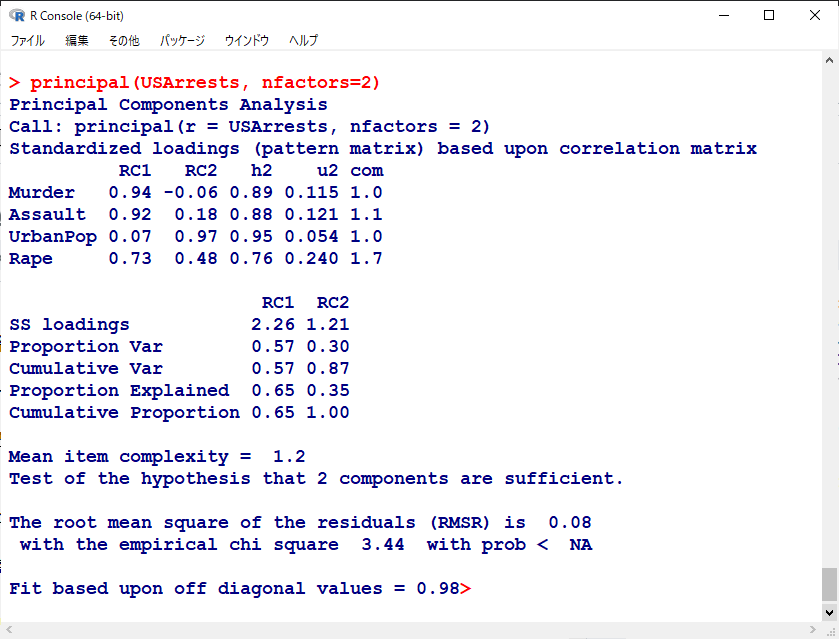
こちらもSPSSの結果と同様である。
主成分プロットは以下のスクリプトで描画できる。
#回転前
biplot(principal(USArrests,nfactors=2,rotate="none"))
#回転後
biplot(principal(USArrests,nfactors=2))
こちらが回転前。
少しだけ軸が傾いている感じがする。
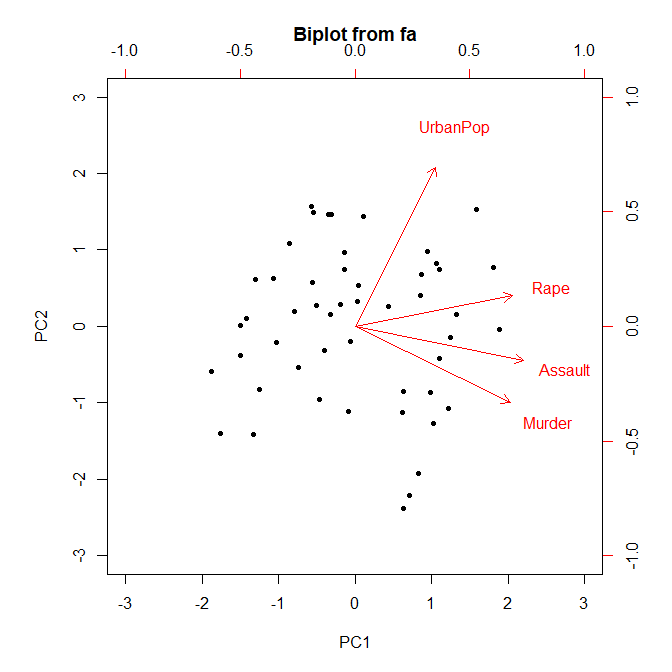
回転後はこんなふうに軸に沿ったプロットになって解釈しやすくなる。
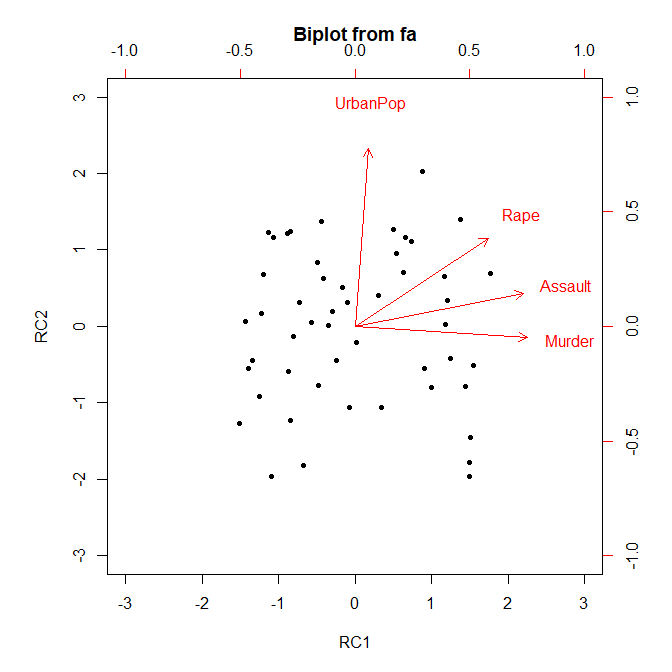
まとめ
主成分分析における軸の回転を、SPSSとRで行う方法を解説した。
因子分析に比べると、主成分分析で軸の回転を行っている解析をあまり見かけないため、少々不安になるが、主成分分析でも軸の回転を行い、主成分負荷量の解釈をしやすくする手法は存在し、実施してかまわない。
SPSSでもRでもいずれも解析可能である。
参考になれば。
参考書籍
SPSSで学ぶ医療系多変量データ解析 第2版









コメント