分散分析のサンプルサイズ計算はあまり知られていないが、多くの人に探されている方法である。
SPSSで計算する方法を紹介する。
分散分析のサンプルサイズ計算はSPSSのどのメニューから実行するか?
メニューは、分析→検定力分析→平均→一元配置分散分析、でたどり着ける。
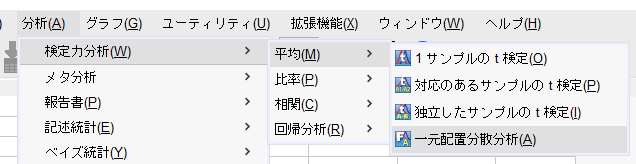
しかし、開いた窓には、何が書いてあるのか、よくわからずどんな数値を入れるのかさっぱりわからない、といったところではないだろうか。
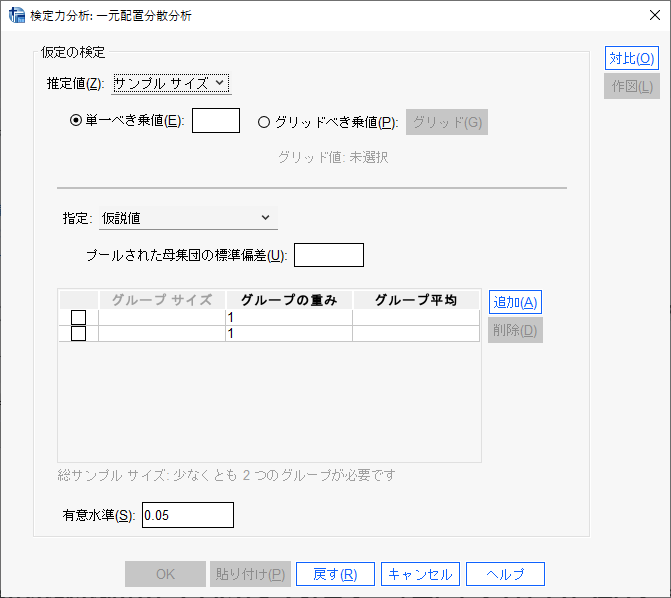
必要な個所を一つ一つ見ていく。
単一べき乗値とは?
ここには検出力を入力する。
通常は0.8でよい。
単一べき乗値は、Single power valueの翻訳と思われる。
Powerは、べき乗の意味もあるが、ここではべき乗ではなく、検出力だ。
指定はCohenのfかイータ2乗を使う
例えば2群の平均値の差であれば、標準偏差で割った標準化した差を効果サイズ(effect size)(効果量とも言う)というが、それと同等の標準化した効果サイズを指定するのがよい。
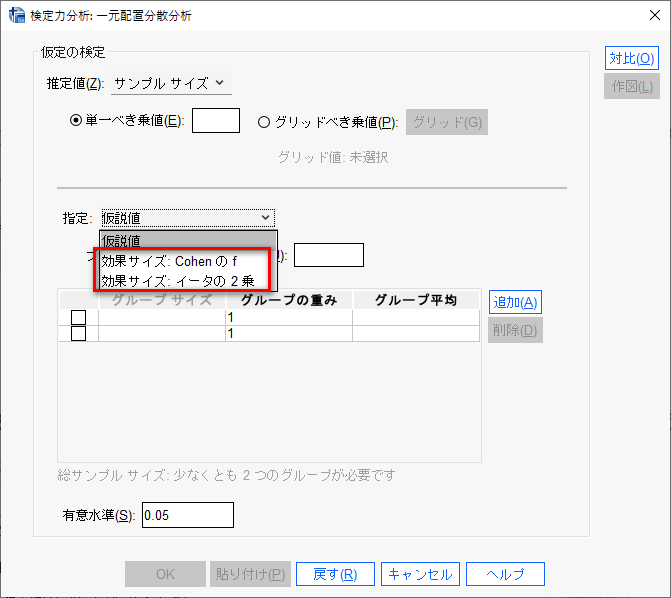
Cohenのfとイータ(η)2乗が選べる。
この2つが何なのか、どうすればよいかを解説する。
Cohenのfは慣例の値がある
先行研究やパイロット研究の結果などの情報が一切ないために、エイヤで決めなければならない場合は、Cohenが提唱してくれている慣例がある。
- Small Effect: f=0.1
- Medium Effect: f=0.25
- Large Effect: f=0.4
これを使うことができる。
イータ2乗はSPSSで分散分析を実施すると計算される
イータ2乗は、SPSSで分散分析を実行すると自動的に計算される。
例えば、分散分析を実行すると以下のような「分散分析の効果サイズ」と呼ばれる表が出力される。
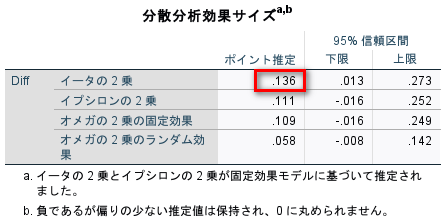
今回の例では0.136である。
パイロット研究データが利用可能な場合は、このようにイータ2乗が計算できるので、本番の試験のためのサンプルサイズ計算ができるというわけである。
また、すでにデータを取得した後に、改めて、必要サンプルサイズ計算が求められた場合は、分散分析が実行できるので、この値を使うことができる。
イータ2乗は、群間の平方和と全体の平方和の比であるので、先行研究の論文に分散分析表が掲載されていれば、そこから計算できる。
今回の例の分散分析表は以下のとおりである。
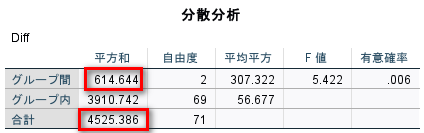
ここでグループ間の平方和 614.644 と合計の平方和 4525.386 の比を計算すると、0.1358213と計算され、先ほどのイータ2乗 0.136 に一致する。
> 614.644/4525.386
[1] 0.1358213
このように分散分析表からイータ2乗は計算できる。
ちなみに、イータ η2乗とfの間には、以下のような関係があるので、イータ2乗がわかればfも計算できる。
今回の場合は、ほぼ0.4でLarge Effectくらいであることがわかる。
$$ f = \sqrt{\frac{\eta^2}{1 – \eta^2}} $$
> eta2 <- 0.136
> f <- sqrt(eta2/(1-eta2))
> f
[1] 0.396746
イータ2乗=0.136を入力して、話を進めていく。
群の数とサンプルサイズ比を入力する
その下のセクションで群の数を必要に応じて追加し、ケースの重みというカラムにサンプルサイズ比を入力する。
今回の例は3群なので、追加をクリックし、3群にした。
サンプルサイズ比は、特に意図がない限り、全群同数がよく、3群であれば1:1:1がよい。
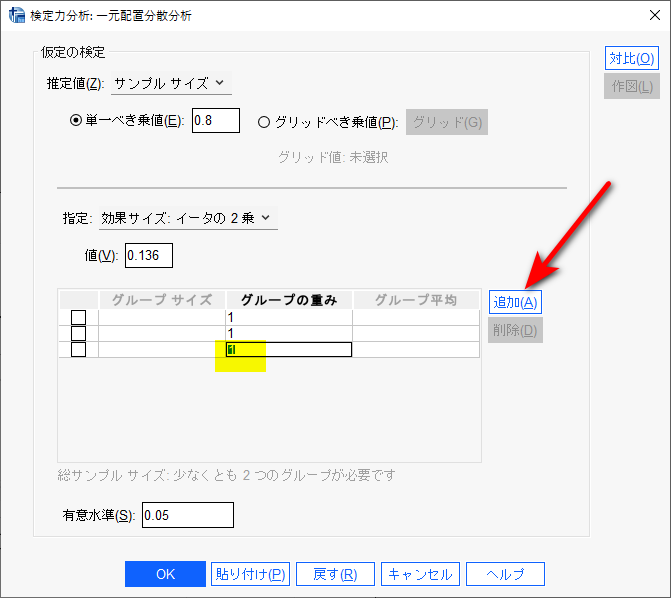
ケースの重みに1を入力した後、Tab キーを押すと、OKがクリックできるようになる。
フォーカスのセルが、例えば右に移ることが、入力されたという合図のようだ。
あとはOKをクリックすると計算される。
(ただし、バグなのか、OKをクリックしても計算されないことがあるので、そういう場合は、いったんキャンセルし、もう一度窓を開いて、同じことを入力してOKをクリックすると計算されたりする。このように、何度が実行してみることが必要なようだ)
(また、Cohenのfに何か入力して計算してみて、実行できることを確認した後、イータ2乗に値を入れて計算したり、まず2群で計算しておいて、計算ができることを確認した後、3群に増やして計算してみたり、いろいろと試行錯誤が必要な場合もある)
出力の解釈
検出力の計算結果と、サンプルサイズの計算結果が同時に出力される。
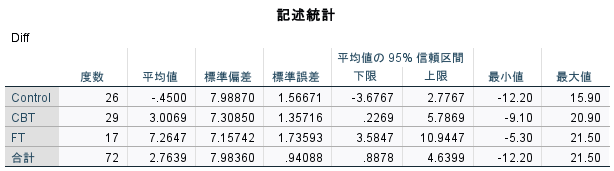
「全体の検定用のグループ サイズ割り振り」というタイトルの表に1群あたりの必要サンプルサイズが表示されている。

今回の例では1群22例、合計で66例必要と計算された。
検出力は80%で計算したわけだが、このサンプルサイズで実際に検定するとした場合の、実際の検出力(SPSSでは検定力と表示されている)が0.811 (81.1%)と計算されている。

ちなみに、今回使用した例題は、各群、17例、26例、29例であり、1群22例必要という条件におおよそあっていたと言える。
まとめ
SPSSで分散分析のサンプルサイズ計算を実行する方法を紹介した。
ポイントは、効果サイズをどのように決めるかである。
まったく見積もれない場合はCohenが提唱した慣例を用いるという方法がある。
先行研究やパイロット研究、すでに取得した研究データが利用可能な場合は、イータ2乗を計算して、それを用いるという方法もある。
なんらか、お役に立てば。
参考書籍・サイト
Jacob Cohen. Statistical Power Analysis for the Behavioral Sciences.
SPSSによる分散分析・混合モデル・多重比較の手順









コメント