G*Power で重回帰分析に必要なサンプル数を計算する方法

G*Power は、サンプルサイズや検出力を計算するソフトウェアである

重回帰分析のサンプルサイズや検出力を計算する方法の紹介

GPower で重回帰分析のサンプル数を計算する方法

重回帰分析のサンプル数を計算するときは、予想される決定係数を見積もる必要がある

先行研究やパイロット研究から、だいたいの値を見積もる必要がある

可能であれば、自由度調整済み決定係数を用いるのが良いと思う

調整していない決定係数よりも小さい値であることから、控えめな計算（サンプルサイズは大きくなる）になるからだ

自由度調整済み決定係数はどのように使うのだろうか？

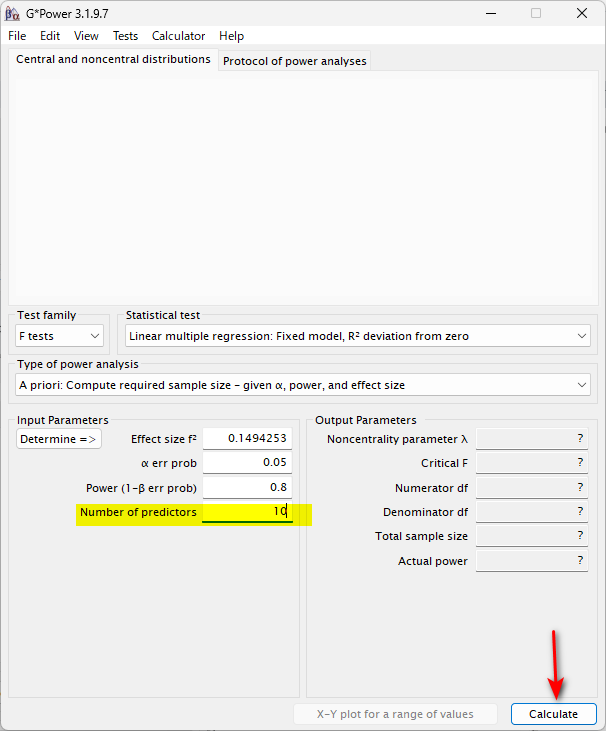
まず、G*Power は下図の黄色ハイライトのように設定する

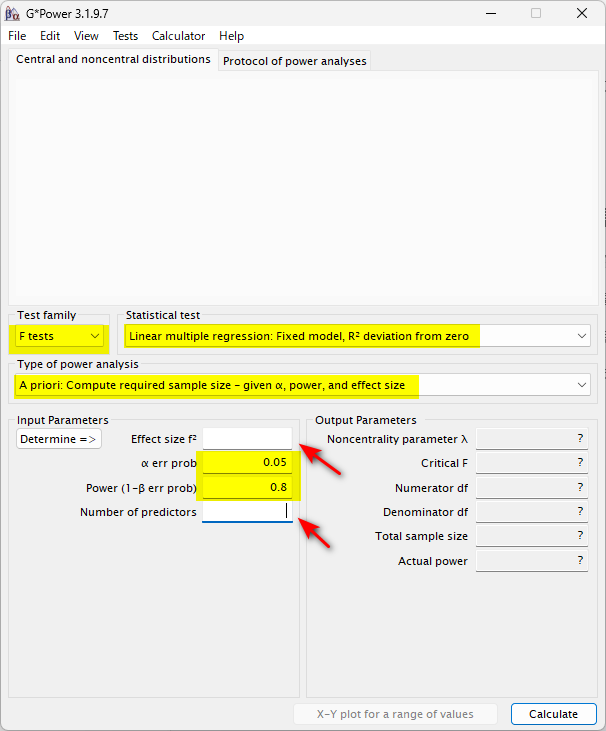
赤矢印のところが決めなければならない数値である

Effect size の設定方法

Effect size f² は、以下の式で計算できる

$$ f^2 = \frac{R^2}{1-R^2} $$

R² が自由度調整済み決定係数である

例えば、R² = 0.13 とすると、f² = 0.149425 となり、約 0.15 と計算される

この数値を Effect size f² に入れる

実は、Effect size は、Determine => ボタンを押すことで出てくるタブ内で計算することができる

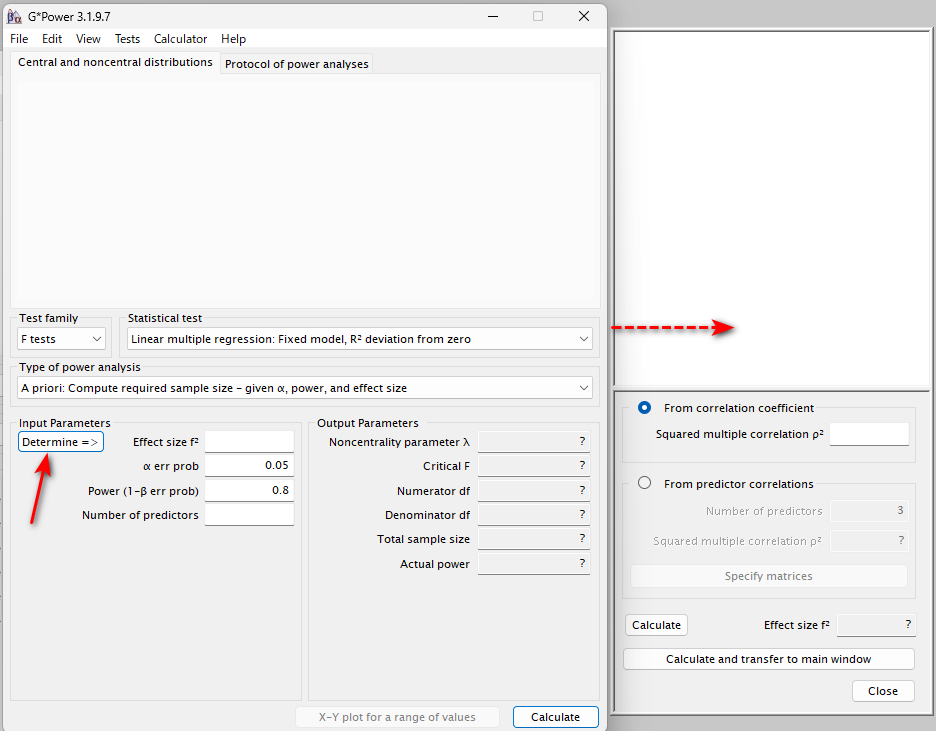
破線矢印が右側のタブの展開を示している

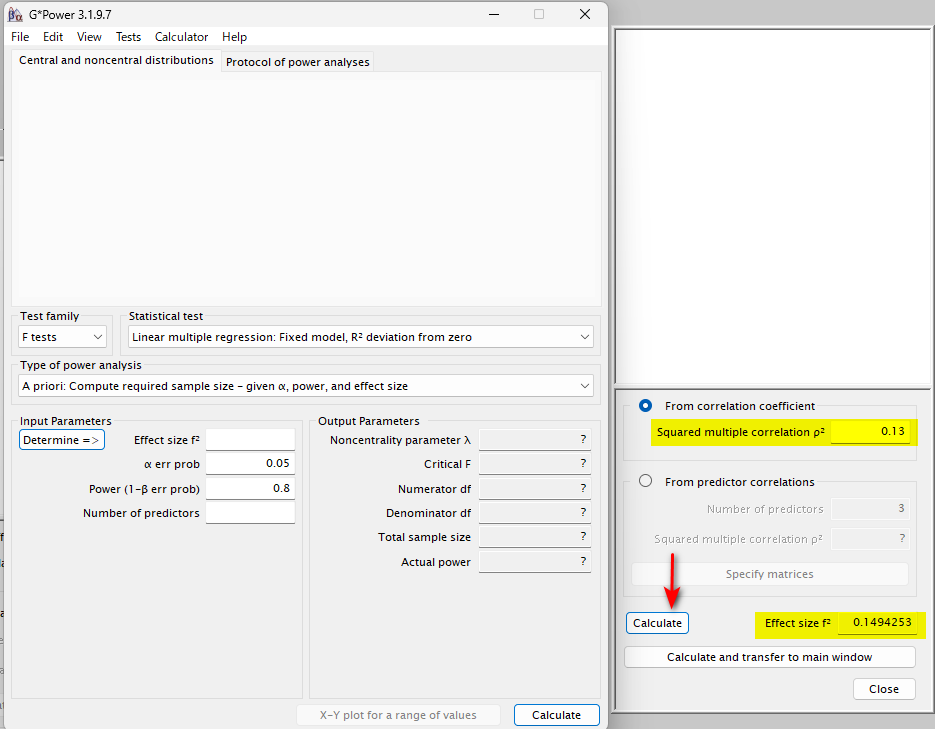
Squared multiple correlation $ \rho^2 $ （ロー 2 乗と読む）に R² の値を入れれて、右タブ内の Calculate をクリックすると Effect size f² が計算される

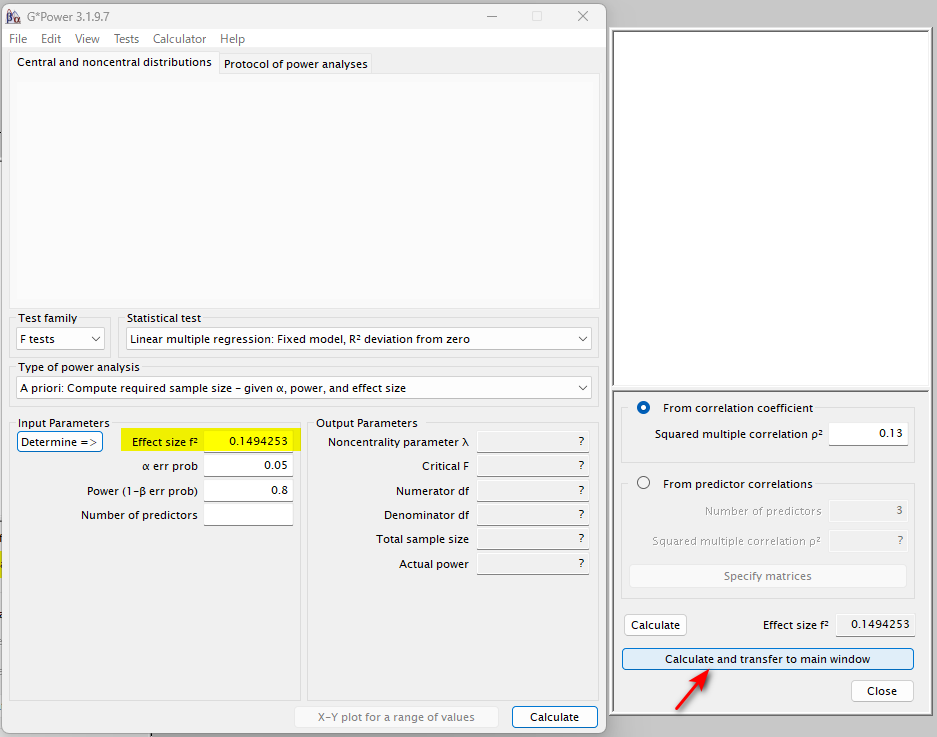
Calculate and transfer to main window をクリックすると、左のメインウィンドの Effect size f² に書き込まれる

Number of predictors の設定方法

これは、想定される説明変数の数のことである

ダミー変数を含む（ダミー変数は 0 と 1 のみの連続データとみなす）、連続データをいくつ投入した重回帰モデルを作成するかを想定して、数字を入れる

10 個の場合は、10 と書き入れる

最後にメインウィンドの Calculate をクリックすると必要サンプルサイズが計算される

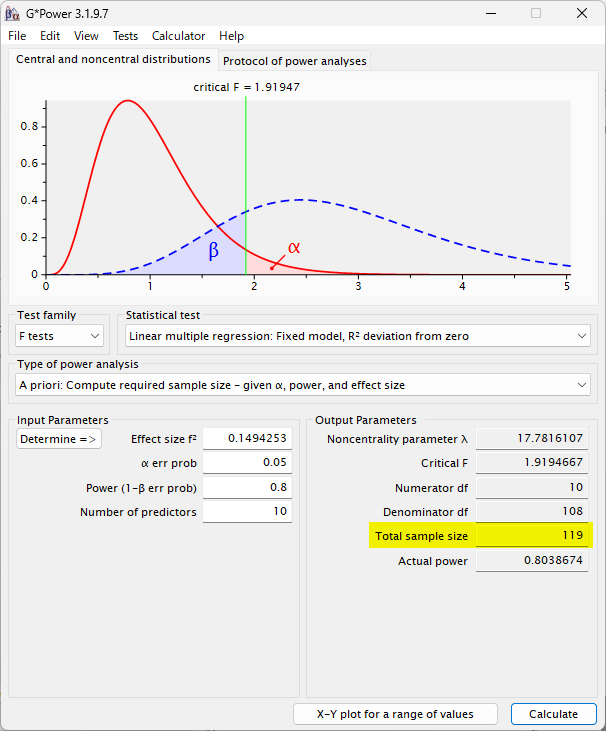
重回帰分析にいくつの説明変数が投入できるかが知りたい場合は、ここの数値を 5、10、15、20 などと変えてみて、必要サンプルサイズがどのように変化するか見てみるのが良い

そうすると、説明変数の増加によって、どのくらいサンプルサイズが要求されるかがわかると思う

Effect size が見積もれないときの慣例

そうはいっても、Effect size がまったく見積もれない場合もあるだろう

そういう場合は、Small size, Medium size, Large size の 3 つの慣例が存在する

R² は、逆算で以下のように計算できる

$$ R^2 = \frac{f^2}{1+f^2} $$

f² の慣例と、そこから逆算で、R² を求めると以下のようになる

Effect size	f2	R2
small	0.02	0.01960784
medium	0.15	0.1304348
large	0.35	0.2592593

慣例の Effect size それぞれは、上記のような R² が得られる重回帰モデルという想定と理解できる

これら慣例の場合のサンプルサイズは、以下のようになる

いずれも、説明変数 10 個とする

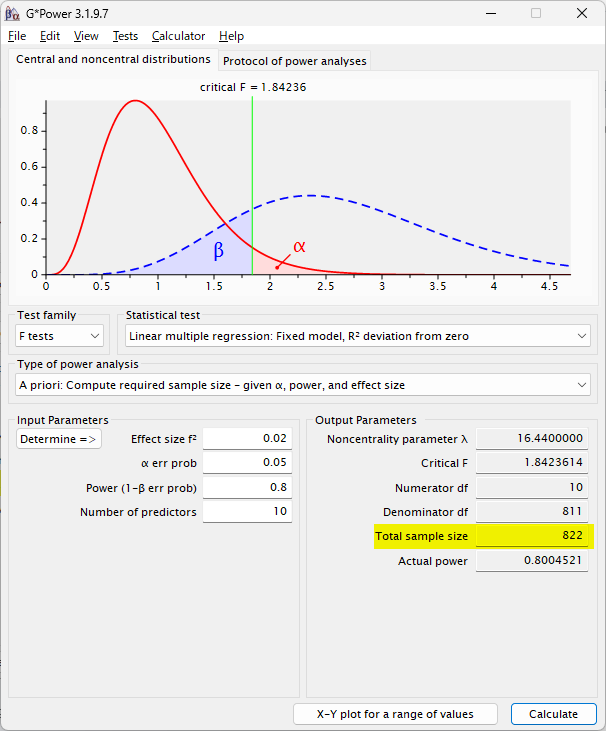
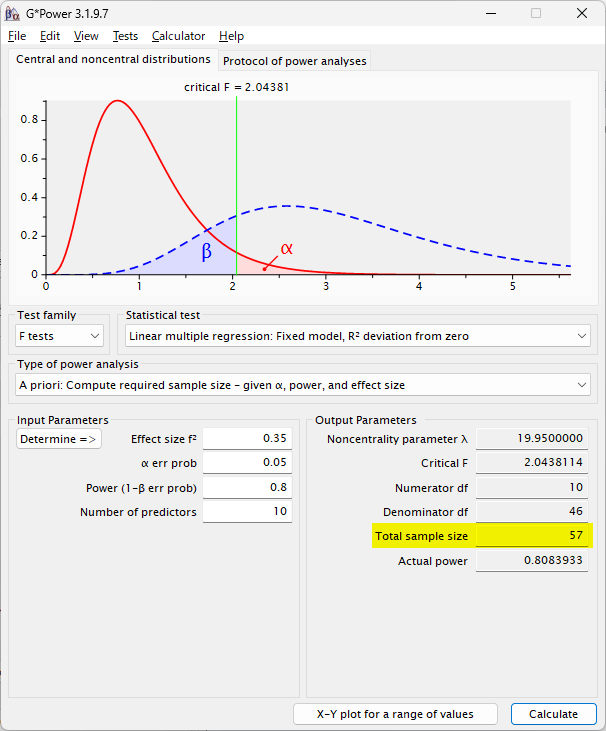
small size = 0.02 の場合は、822 例必要と計算される

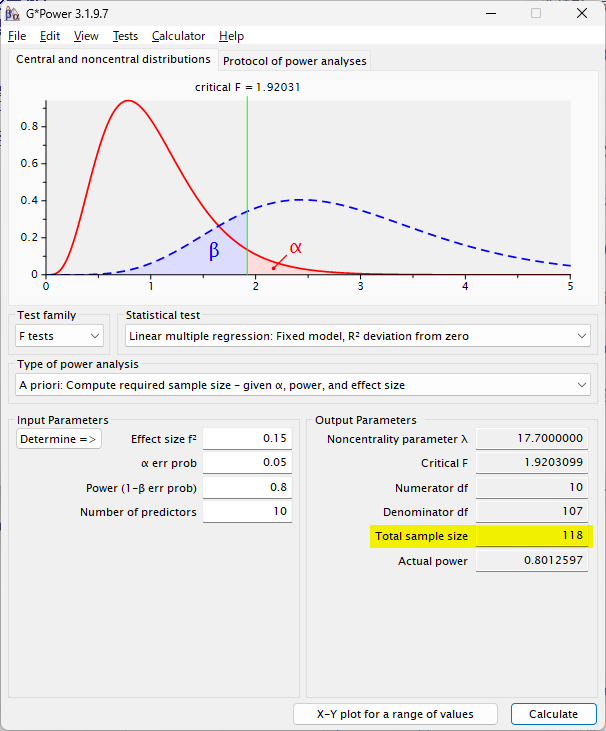
medium size = 0.15 の場合は、先ほどとほぼ同様の 118 例必要と計算される

large size = 0.35 の場合は、57 例でよいという計算になる

論文への記述方法

上記の Medium effect size のときの計算結果を論文に記述する際の例文を書いてみる

サンプルサイズ計算は、G*Power 3.1.9.7 で行った（Faul 2007, Faul 2009）。偏回帰係数を推定したい説明変数の個数を 10 とした重回帰モデルにおいて Effect size f² = 0.15（Cohen 1988）（自由度調整済み決定係数 R² = 約 0.13）が得られるとし、有意水準 5 %、検出力 80 ％ で検定すると想定したときに、必要サンプルサイズは合計 118 例と計算された。

The sample size calculation was performed using G*Power 3.1.9.7 (Faul 2007, Faul 2009) . Assuming a multiple regression model with 10 explanatory variables for which we want to estimate the partial regression coefficients, and given an effect size of f² = 0.15 (Cohen 1988) (adjusted coefficient of determination R² ≈ 0.13) is obtained, when testing at a significance level of 5% and a power of 80%, the required sample size was calculated to be a total of 118 cases.

事後検出力の計算方法

現実には、サンプルサイズ計算をしない段階で、データはすでに取得してあり、統計解析したところ、自由度調整済み決定係数が小さく、モデル自体が統計学的に有意ではない状態になることもある

そのような場合に、事後検出力の確認を求められる時がある

その場合には、以下の黄色ハイライトのように、Type of power analysis を Post hoc に変更する

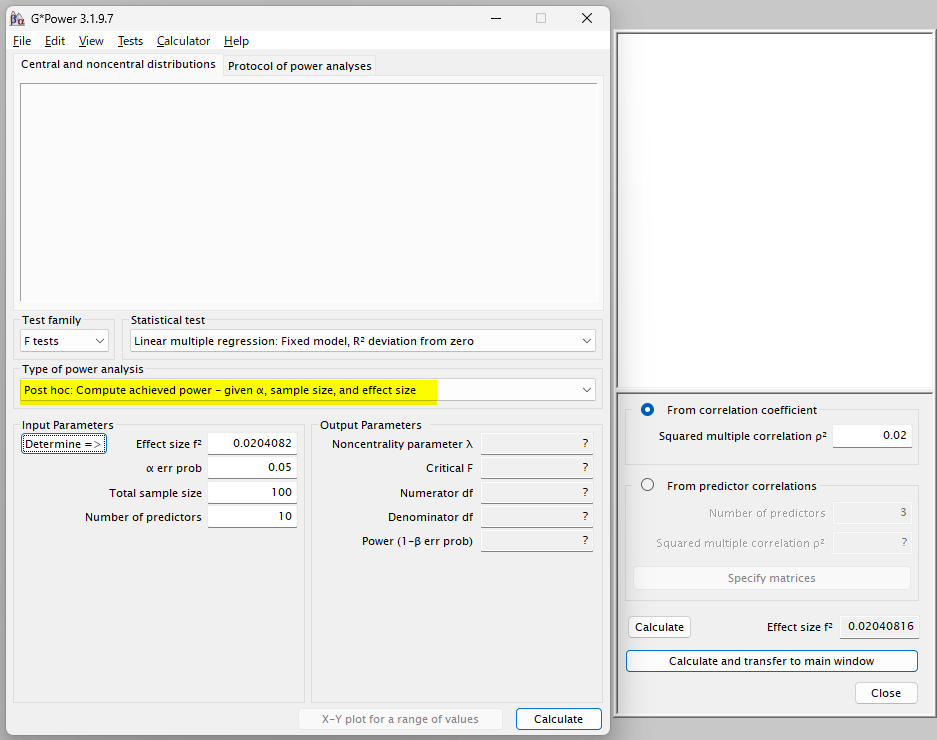
説明変数が 10 個の重回帰モデルで、自由度調整済み決定係数が約 0.02 であり、Effect size f² も 0.02/(1-0.02) = 0.02040816 と計算されたとする

サンプルサイズが 100 例であったとすると、検出力は約 11 ％ と計算される

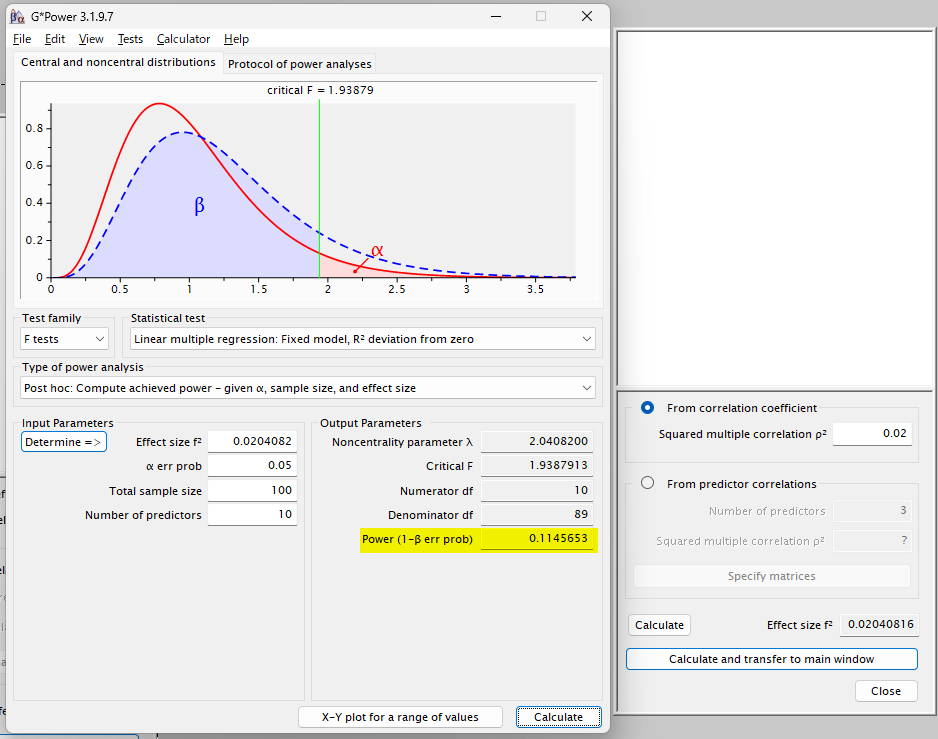
サンプルサイズの観点では、今回のサンプルではサイズが小さく、検出力が約 11 ％ しかなかったと考察する形になる

このような場合、目的変数をよりよく説明できる（もっと自由度調整済み決定係数が大きくなる）説明変数の取得が必要だったとも言えるだろう

より大きな自由度調整済み決定係数が得られていれば、サンプルサイズが小さくても、統計学的に意味がある重回帰モデルが得られるからだ

まとめ

G*Power を使って、重回帰分析のサンプルサイズ計算と事後検出力の計算を実施する方法を紹介した

参考になれば

参考文献

Cohen 1988

G*Power ダウンロードサイト

Universität Düsseldorf: G*Power