G*Power は、サンプルサイズや検出力を計算するソフトウェア
分散分析の場合のサンプルサイズや検出力の計算方法の紹介
GPower で分散分析のサンプル数を計算する方法
3 群以上の群があるときに、いずれかの群が異なるかどうかを検討する場合に使う、一元配置分散分析のときの必要サンプル数計算の方法を紹介する
G*Power の設定は、下図の黄色ハイライトのように行う
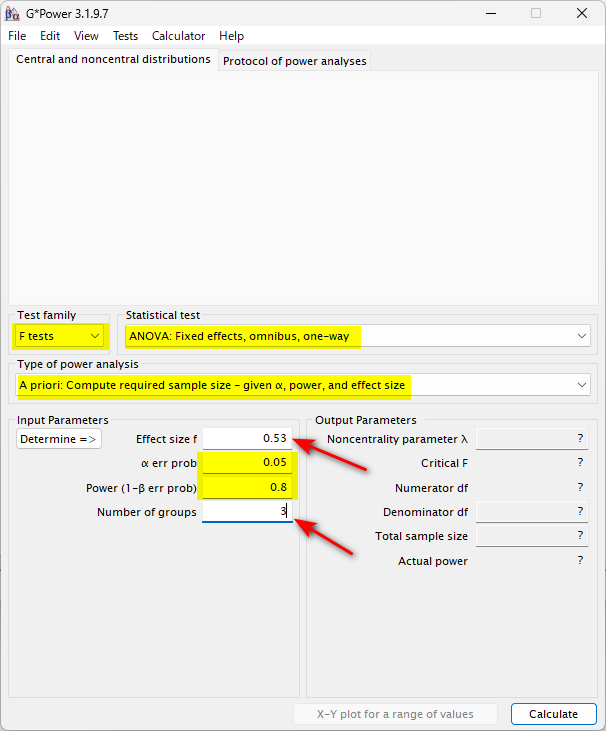
Number of groups は、群の数なので、これはわかりやすい
難しいのは、Effect size f である
Effect size f を計算する方法
Effect size f は以下の式で計算できる
$$ f = \sqrt{\frac{\eta^2}{1-\eta^2}} $$
ここで、$ \eta^2 $ は、イータ 2 乗と読む
イータ 2 乗は、グループ間の平方和と合計の平方和の比である
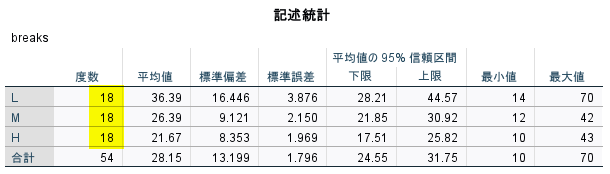
具体的には、下図分散分析表における、黄色ハイライトにした数値の比のことである
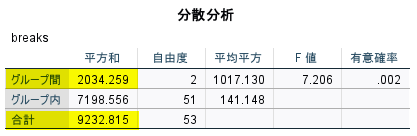
これが分散分析の効果量の一つとなる
計算してみると、2034.259 / 9232.815 = 0.2203292 となる
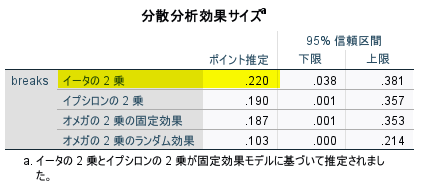
このイータ 2 乗を、$ f = \sqrt{\frac{\eta^2}{1-\eta^2}} $ の式で計算すると、f = 0.5315944 と約 0.53 と計算できる
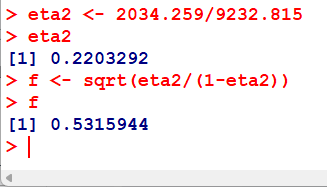
右下の Calculate をクリックすると計算される
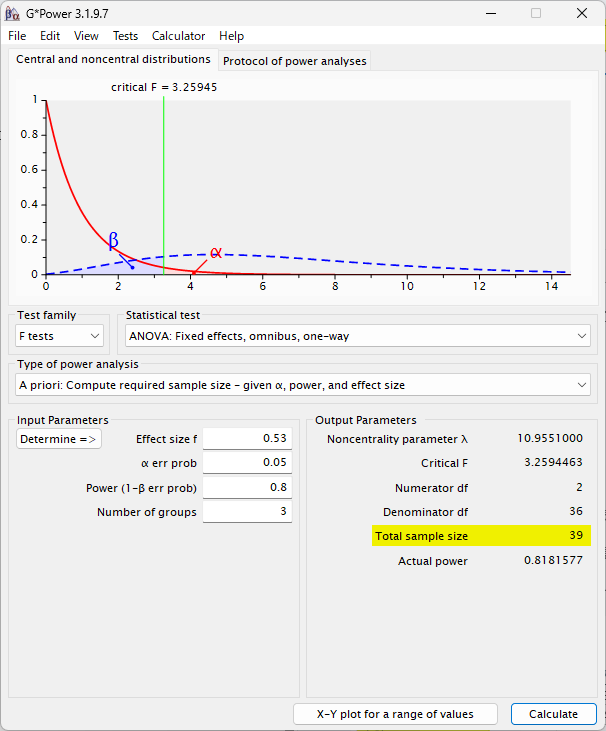
結果、全体で 39 例必要と計算されるので、一群 13 例必要という計算になる
例に用いたデータセットは、一群 18 例であったので、十分に有意差が検出できるサンプル数だったと言える
ただし、先行研究で、分散分析表が掲載されることはまれだろう
小規模なパイロット研究を行った結果が手元にあれば、計算できるだろうが、必ずしも手に入るとも限らない
そのように、Effect size が見積もれない場合は、どうしたらよいだろうか?
Effect size が見積もれない場合のサンプル数計算
Effect size が見積もれない場合、Effect size が、小さい、中程度、大きいと考えた場合の慣例が存在する
以下の表のとおりである
| Effect size | f |
|---|---|
| small | 0.1 |
| medium | 0.25 |
| large | 0.4 |
Small effect size f = 0.1 の場合は、3 群で 969 例必要と計算される
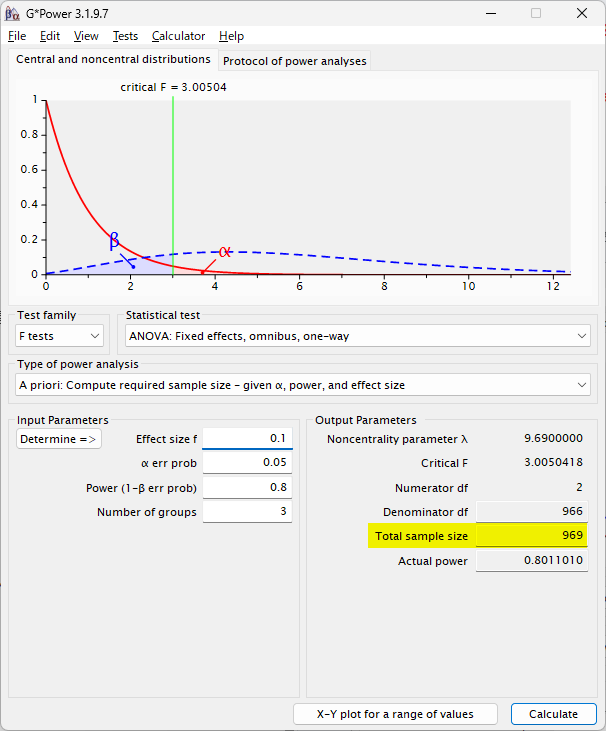
Medium effect size f = 0.25 の場合は、3 群で 159 例必要
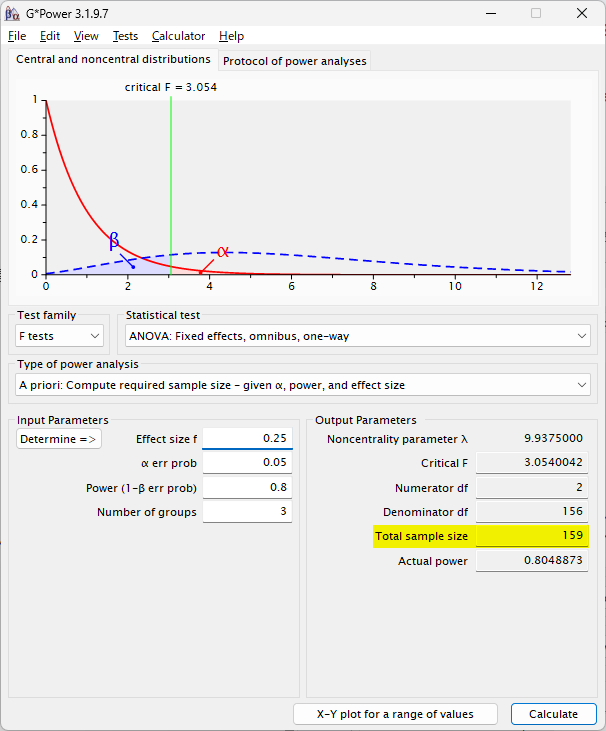
Large effect size f = 0.4 の場合は、3 群で 66 例必要となる
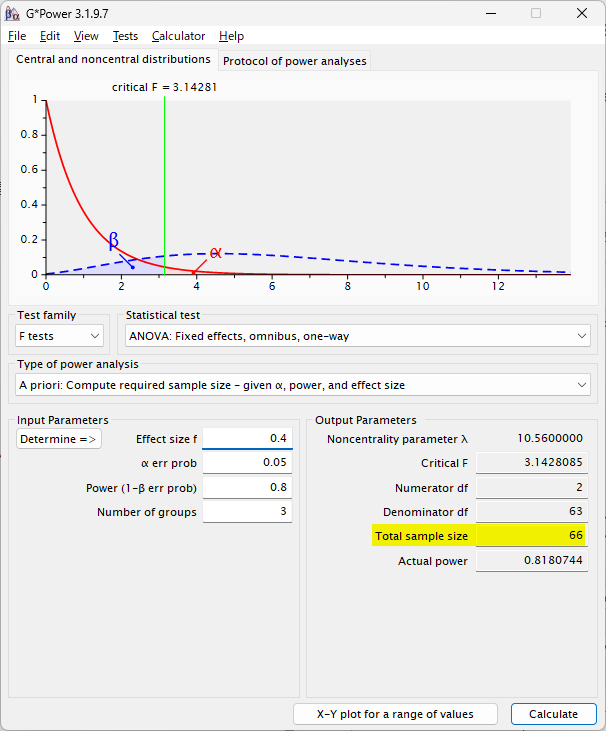
サンプルサイズ計算の記述例
論文にサンプルサイズ計算について記述する場合、以下のような文章にて書くことができる
サンプルサイズ計算は、G*Power 3.1.9.7 で行った(Faul 2007, Faul 2009)。3 群の一元配置分散分析を実施することとし、効果量 0.25、有意水準 5 %、検出力 80 % としたときに、必要サンプルサイズは合計 159 例と計算された。
The sample size calculation was performed using G*Power 3.1.9.7 (Faul 2007, Faul 2009) . Assuming a one-way anlysis of variance between three groups with a effect size of 0.25, a significance level of 5%, and a power of 80%, the required sample size was calculated to be 159 cases.
事後的に検出力を計算する方法
もしも、有意差が検出できなかった場合、事後的にどのくらいの検出力だった確認することができる
例えば、Effect size が中程度の f = 0.25 であった場合に、サンプル数が各群 22 例ほどしか集まらず、有意差が検出できなかったとする
その場合は、Type of power analysis を A priori から Post hoc に変更する
Effect size を 0.25、Total sample size は各群 22 例で、合計 66 例とする
計算すると、0.4093002 となり、約 40 %ほどの検出力しかなかったことがわかる
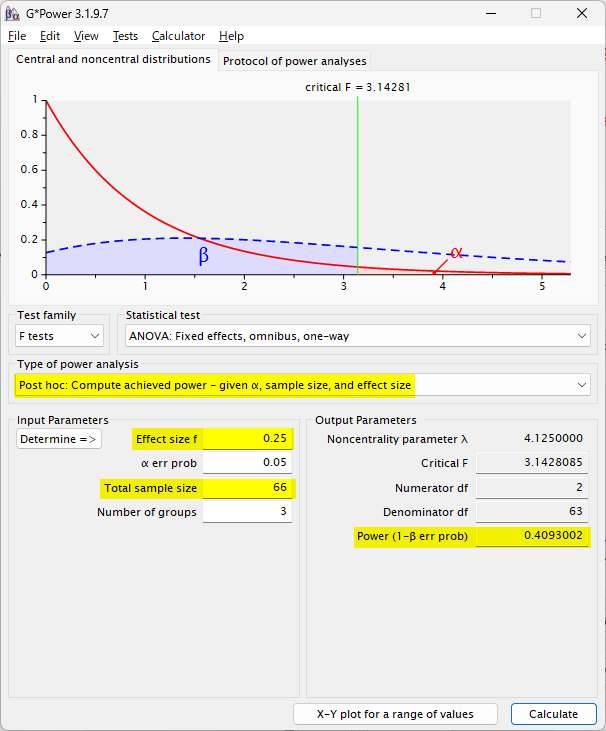
このような場合は、サンプル数不足による検出力不足で、有意差が検出できなかったという考察になる
まとめ
G*Power を使って、一元配置分散分析のサンプル数及び事後検出力の計算方法を紹介した
参考になれば
参考文献
http://www.utstat.toronto.edu/~brunner/oldclass/378f16/readings/CohenPower.pdf








コメント