GPower は、サンプル数を計算するソフトウェアである
事後検出力を計算することもできる
対応のある t 検定の場合の使い方を紹介
GPower で 対応のある t 検定のサンプル数を計算する方法
対応のある t 検定を使って、同じ人から 2 回測定して、その差を検定する場合を考える
GPower は、以下の黄色ハイライトのように設定する
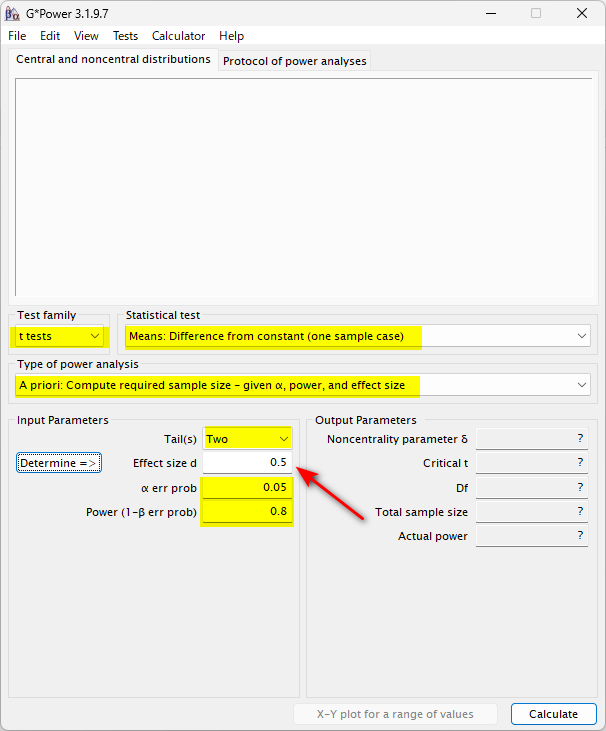
問題は、赤矢印の Effect size と思う
Effect size 0.5 というのは、2 回の差の平均値が 例えば 5 だとして、標準偏差が 10 の時に 5 / 10 = 0.5 と予想されるという意味である
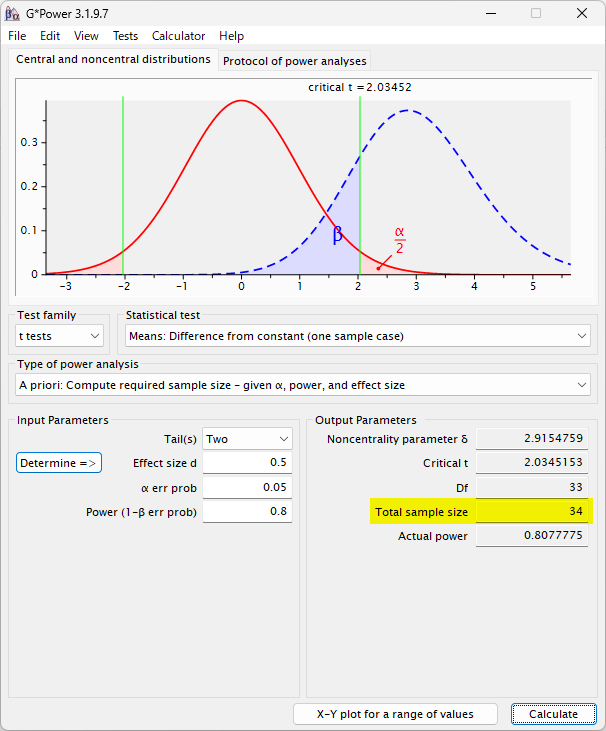
これで計算すると以下のように 34 例必要と計算される
Effect size の慣例
先行研究やパイロット研究から差の平均値や標準偏差が得られない場合、以下の慣例的な Effect size が利用可能である
| Effect size | d |
|---|---|
| small | 0.2 |
| medium | 0.5 |
| large | 0.8 |
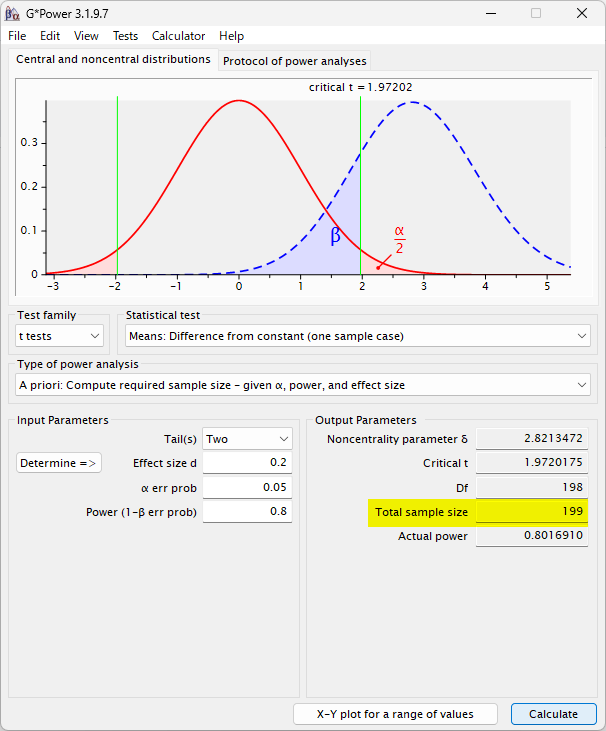
0.2 とすると、以下のように 199 例必要と計算される
0.5 は、上記のとおり 34 例である
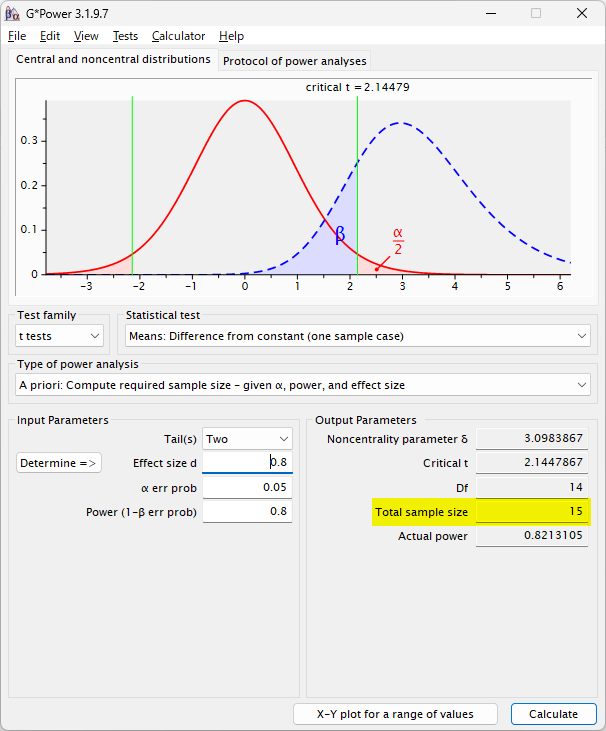
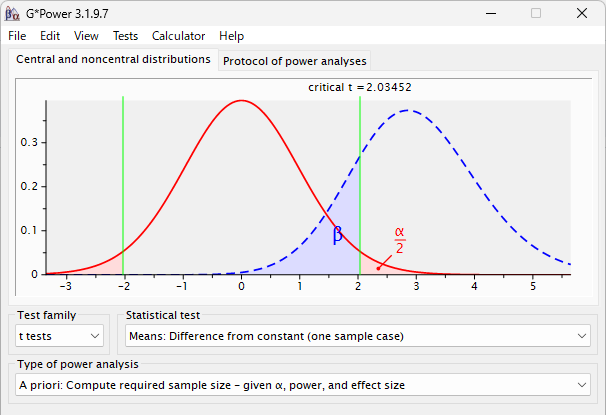
0.8 とすると、以下のように 15 例必要となる
サンプルサイズ計算の記述例
例えば、論文の方法の章の統計解析セクションには以下のように書くことができる
サンプルサイズ計算は、G*Power 3.1.9.7 で行った(Faul 2007, Faul 2009)対応のある t 検定を、両側検定で実施し、効果量 0.5、有意水準 5 %、検出力 80 % としたときに、必要サンプルサイズは 34 例と計算された。
The sample size calculation was performed using G*Power 3.1.9.7 (Faul 2007, Faul 2009) . Assuming a two-tailed paired t-test with a effect size of 0.5, a significance level of 5%, and a power of 80%, the required sample size was calculated to be 34 cases.
必要に応じて、効果量をどのように見積もったか、加筆してもよいだろう
事後検出力の計算
データを取得して統計解析を行うも、統計学的有意とならなかった場合、事後検出力を求められることがあるだろう
その場合は以下のように計算することができる
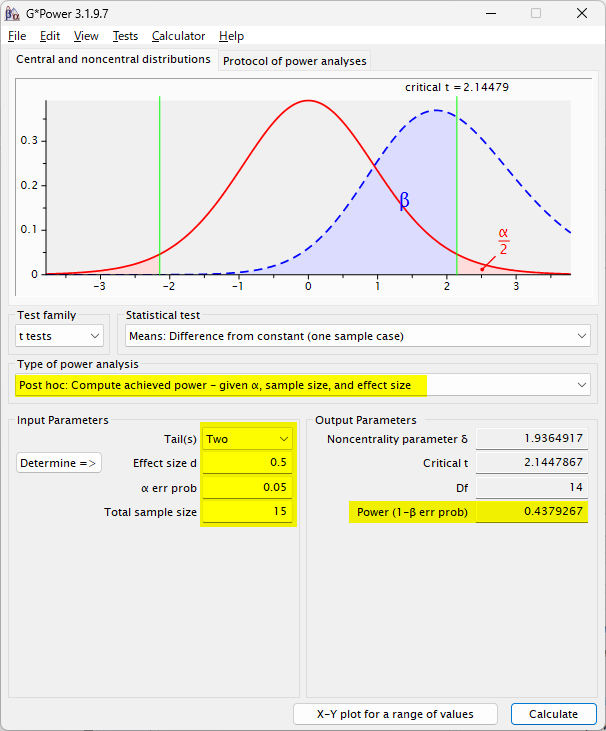
Type of power analysis を Post hoc に変更する
Effect size が 0.5 であるが、サンプル数が 15 しか集まらなく、統計学的有意でもなかった場合、事後的に計算した検出力は、0.4379267 で 約 44 % であったと計算される
本来、80 % が望ましいので、44 % しかなかったため、検出できなかったと考察できるだろう
まとめ
G*Power を使って、対応のある t 検定の必要サンプル数計算、慣例的な Effect size の紹介、論文への記述例、事後検出力の計算を紹介した
参考になれば








コメント