相関係数の計算に必要なサンプル数はいくつか?
相関係数の検定との関係から紹介。
相関係数のサンプル数計算の前提となる検定の計算方法
相関係数の検定は、母集団の相関係数、母相関係数(ぼそうかんけいすう)がゼロかどうかの検定である。
通常はt分布を使う検定統計量tを計算する。rは相関係数、nはデータのペア数(サンプルサイズと言う。サンプル数とも言われる)。
$$ t = \frac{|r| – 0}{\sqrt{\frac{1 – r^2}{n – 2}}} $$
rはフィッシャーのz変換という変換を施すことで、正規分布に従う変数に変換できる。z変換は以下の通り。
$$ z = \frac{1}{2} \log{\frac{1 + r}{1 – r}} $$
zは分散 \frac{1}{n – 3} に従う。よって母相関係数がゼロであると想定した場合、以下のように標準化できる。
$$ Z = \frac{z – 0}{\sqrt{\frac{1}{n – 3}}} $$
このZを用いて、標準正規分布で検定することができる。
相関係数のサンプル数計算
相関係数計算に必要なデータのペア数は、上記のZの式をnについて解く。
$$ Z = z \sqrt{n – 3} $$
両辺を 2 乗して
$$ Z^2 = z^2 (n – 3) $$
n について解くと
$$ n = \left( \frac{Z}{z} \right)^2 + 3 $$
ここで、母相関係数がゼロではないという対立仮説分を加える。
先ほどまでのZを帰無仮説のZaとすると、対立仮説のZはZbである。
「Zb分の下駄をはかせて統計学的有意にしやすくする(ぼんやりもの(b)のエラーを減らす)」と覚えるとよい。
$$ n = \left( \frac{Z_a + Z_b}{z} \right)^2 + 3 $$
これが必要サンプルサイズになる。
計算に必要な情報は、相関係数r(これをz変換する)、有意水準α(Zaを計算する)、検出力1-β(Zbを計算する)、検定が両側か片側かである。両側の場合はαを半分にして使う。
相関係数の計算と検定をRで行う方法
相関係数の例を提示して、その結果を得るためのサンプルサイズ計算を行ってみる。
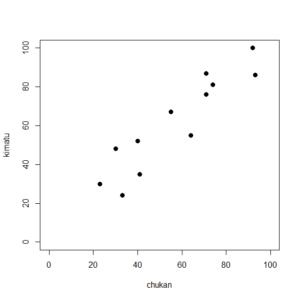
中間テストと期末テスト(架空例)の相関係数を計算してみる。
統計ソフトRを使う。
chukan <- c(64,40,71,33,30,71,92,23,41,55,93,74)
kimatu <- c(55,52,76,24,48,87,100,30,35,67,86,81)
(r <- sum((chukan-mean(chukan))*(kimatu-mean(kimatu)))/(sqrt(sum((chukan-mean(chukan))^2))*sqrt(sum((kimatu-mean(kimatu))^2))))
(n <- length(chukan))
(t <- (abs(r)-0)/sqrt((1-r^2)/(n-2)))
(p_t <- pt(t, n-2, lower.tail=FALSE)*2)
cor.test(chukan,kimatu)
この計算結果は以下の通り。
rは0.9194158で、nは12、tは7.392692、p値は $ 2.33485 \times 10^{-5} $ となる。
ちなみに、cor.test()を使えば、全部一度に計算してくれる。
> (r <- sum((chukan-mean(chukan))*(kimatu-mean(kimatu)))/(sqrt(sum((chukan-mean(chukan))^2))*sqrt(sum((kimatu-mean(kimatu))^2))))
[1] 0.9194158
>
> (n <- length(chukan))
[1] 12
>
> (t <- (abs(r)-0)/sqrt((1-r^2)/(n-2)))
[1] 7.392692
>
> (p_t <- pt(t, n-2, lower.tail=FALSE)*2)
[1] 2.33485e-05
>
> cor.test(chukan,kimatu)
Pearson's product-moment correlation
data: chukan and kimatu
t = 7.3927, df = 10, p-value = 2.335e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.7314858 0.9775232
sample estimates:
cor
0.9194158
このときz変換を使うとどういう結果になるか?
通常は計算しないがサンプルサイズ計算の前段階として計算してみる。
(z <- 1/2*log((1+r)/(1-r)))
(Z <- z/sqrt(1/(n-3)))
(p_z <- pnorm(Z, lower.tail=FALSE)*2)
結果は以下のようになる。
p値は先ほどより少し小さく$ 1.977492 \times 10^{-6} $ である。
> (z <- 1/2*log((1+r)/(1-r)))
[1] 1.585237
>
> (Z <- z/sqrt(1/(n-3)))
[1] 4.755711
>
> (p_z <- pnorm(Z, lower.tail=FALSE)*2)
[1] 1.977492e-06
相関係数のサンプル数計算をRで行う方法
上記の例のように相関係数0.92が統計学的有意(母相関係数がゼロではない)となるためには必要なデータ数はいくつだろうか?
相関係数を0.92、有意水準を両側で5%、検出力を80%とすると以下のように計算できる。
alpha <- 0.05
side <- 2
power <- 0.8
r <- 0.92
(Za <- qnorm(alpha/side, lower.tail=FALSE))
(Zb <- qnorm(power))
(z <- 1/2*log((1+r)/(1-r)))
(n <- ((Za+Zb)/z)^2+3)
結果は以下のとおりである。必要なデータ数(ペア)は6.108459なので切り上げて、7である。
相関係数が0.92くらいなのであれば、12ペアは必要なかったということになる。
7ペアで、相関係数0.92が得られれば、もっとも無駄がない調査デザインだったと言えるわけだ。
> alpha <- 0.05
> side <- 2
> power <- 0.8
> r <- 0.92
>
> (Za <- qnorm(alpha/side, lower.tail=FALSE))
[1] 1.959964
> (Zb <- qnorm(power))
[1] 0.8416212
> (z <- 1/2*log((1+r)/(1-r)))
[1] 1.589027
>
> (n <- ((Za+Zb)/z)^2+3)
[1] 6.108459
相関係数の計算と検定をEZRで行う方法
統計ソフトRをメニューから操作できるように改良されたEZR(イージーアール)でも相関係数の計算と検定はできる。
必要なデータペア数の計算メニューは見つからない。
先ほどの中間・期末テストの点数(架空)例を読み込んで、計算してみる。
EZRのデータの読み込み
「ファイル」→「データのインポート」→「ファイルまたはクリップボード、URLからテキストデータを読み込む」でデータの読み込みを行う。
CSV(カンマ区切りファイル)の場合は何もいじらずOKをクリックする。
開いた窓で読み込むファイルを指定する。
今回はcor-sample.csvというファイルを読み込む。
読み込んだ後の状態は以下の通り。
中央上部の「表示」ボタンをクリックすると読み込んだファイルが表示できる。
中央上部の「表示」ボタンをクリックすると、読み込んだファイルが表示される。
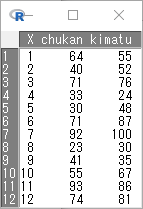
EZRの相関係数計算と検定
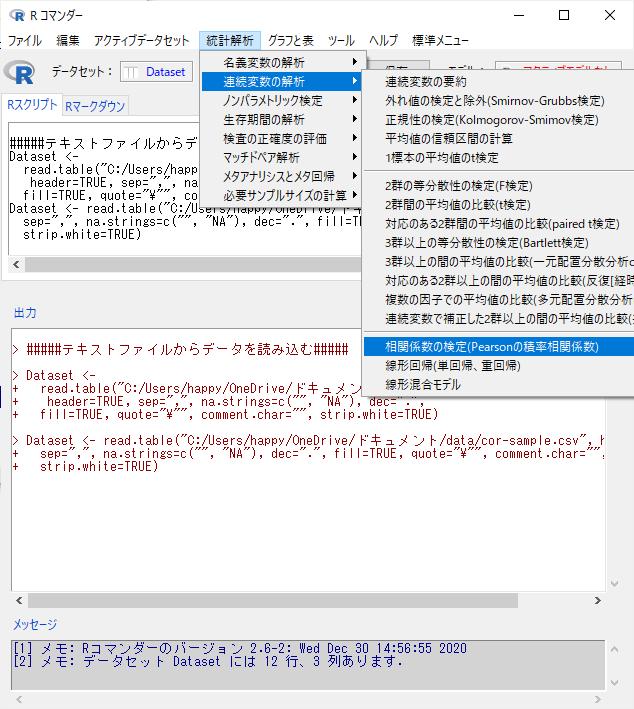
「統計解析」→「連続変数の解析」→「相関係数の検定(Pearsonの積率相関係数)」を選択する。
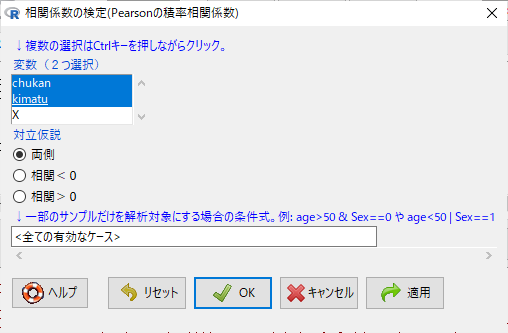
Ctrlキーを押しながら、chukanとkimatuをクリックする。
その後OKをクリックすると計算結果が表示される。
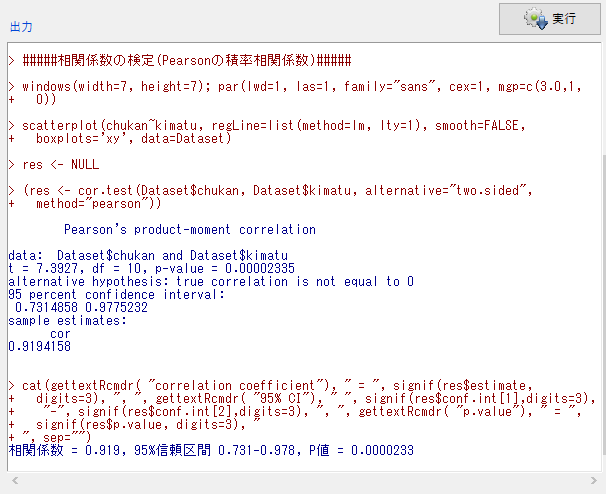
結果の一部を抜き出して解説すると、
sample estimates:
cor
0.9194158
が相関係数の計算結果。
t = 7.3927, df = 10, p-value = 0.00002335
の右端のp-valueがp値で、検定結果。
グラフが自動で表示されるが、散布図だけでなく回帰直線が表示されるため、誤解しやすいので見ないのが望ましい。相関係数と回帰直線は本来別物だ。
相関と回帰については、以下も参照のこと。

相関係数の計算、検定、サンプル数計算をエクセルで行う方法
相関係数の計算、検定、必要なデータ数の計算をエクセルでやってみる。
エクセルシートの全体像は以下の通り。
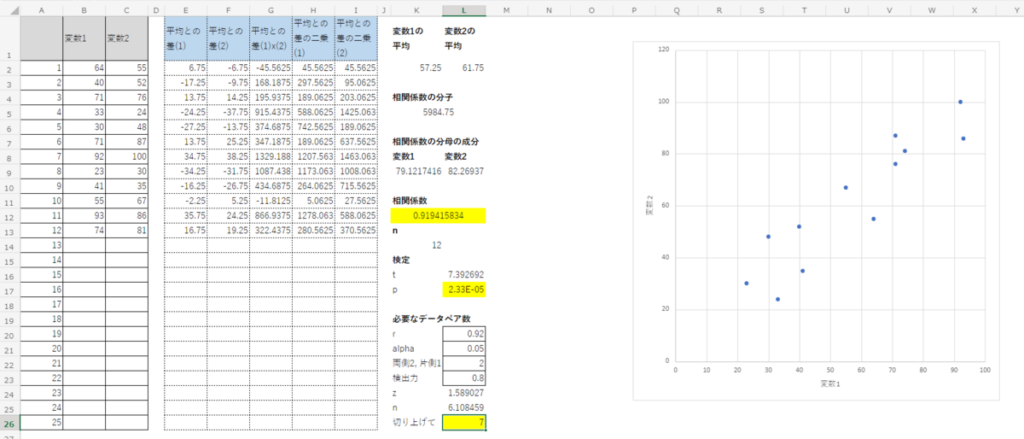
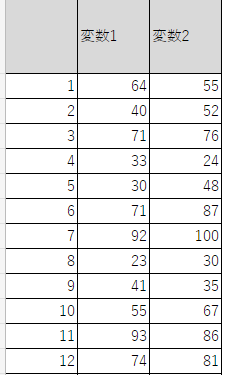
まず、相関係数を計算したいデータペアを入力する。このシートでは25例まで対応可能。
データを入力すると相関係数を計算するのに必要な計算を自動で行ってくれる。
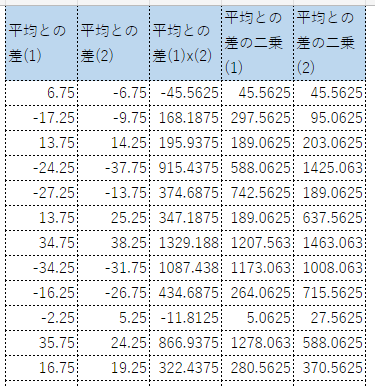
13番目から25番目のデータには式がコピーされていないので、13番目から25番目にデータを入力した場合は、12番目から式をコピー&ペーストする必要がある。
相関係数は、こんな面倒な計算をせずとも =CORREL() を使えば簡単に計算できるのは言うまでもない。
しかし、このように地道に計算してみると、相関係数がどんなふうに計算されているかが実感できて、理解が進むことは間違いない。
一度は地道に計算してみることをお勧めする。
データが入力されると、自動的に相関係数と、検定結果が計算される。
黄色でハイライトされている部分が結果だ。
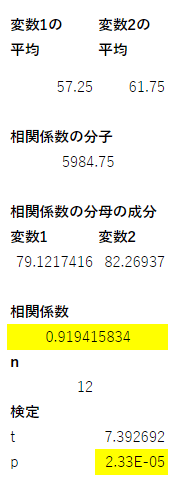
ちなみにp値のE-05というのは $ \times 10^{-5} $ という意味で、10の何乗をEと表現するのは、小数点以下が多くなった時やとても桁が多い大きな数字のときに表示される。
必要なデータペア数の計算は、以下の通り。
nには小数点以下があるが、切り上げれば想定した検出力以上が保てるため、切り上げるのがよい。
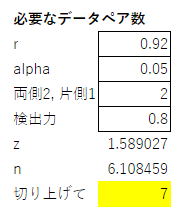
予測される相関係数r、有意水準(通常は0.05のままでよい)、両側検定か片側検定か(通常は両側)、検出力(通常は0.8のままでよい)を入力すると、zが計算され、nが計算される。
ちなみに、この必要なデータペア数計算の部分は左側の計算シートとは関係ない。rは自分で自由に変えることができる。
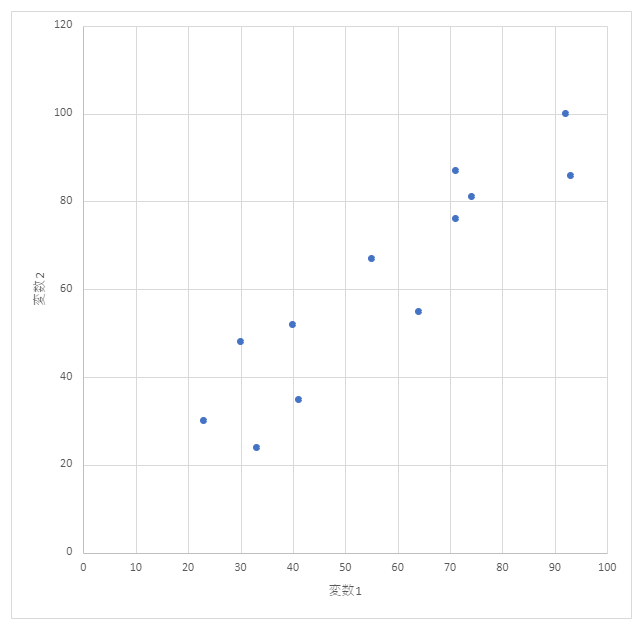
エクセルシートの右側は散布図である。データを入力すると自動で描かれる。
もしこのエクセルシートが欲しいという希望があれば購入できる。
実際にどんな関数が使われていて、どんな計算が行われているかを確認することができ、相関係数の理解が進むと思う。
よければどうぞ。
相関係数の計算・検定・必要なデータペア数 計算エクセルシート | TKER SHOP
相関係数の計算・検定・サンプル数計算 エクセルシート 使い方解説【動画】
相関係数の計算、検定、サンプル数計算をSPSSで行う方法
まず上記RのデータをCSVファイルに変換してSPSSへもっていく。
chukan <- c(64,40,71,33,30,71,92,23,41,55,93,74)
kimatu <- c(55,52,76,24,48,87,100,30,35,67,86,81)
dat <- data.frame(chukan,kimatu)
write.csv(dat, "chukan_kimatu.csv")
デフォルトであるとWindowsのドキュメントフォルダにCSVファイルが作成されるので、それをSPSSに読み込む。
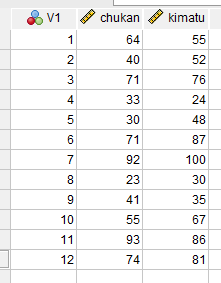
「分析」→「相関」→「2変量」を選択。
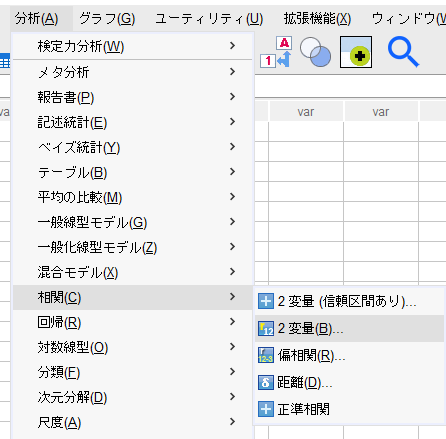
chukanとkimatuを両方選択して右矢印で投入。
投入したところ。
OKをクリックすると計算結果が出力される。
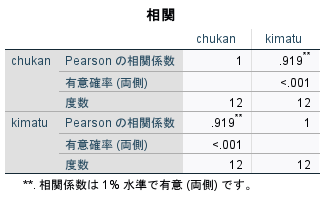
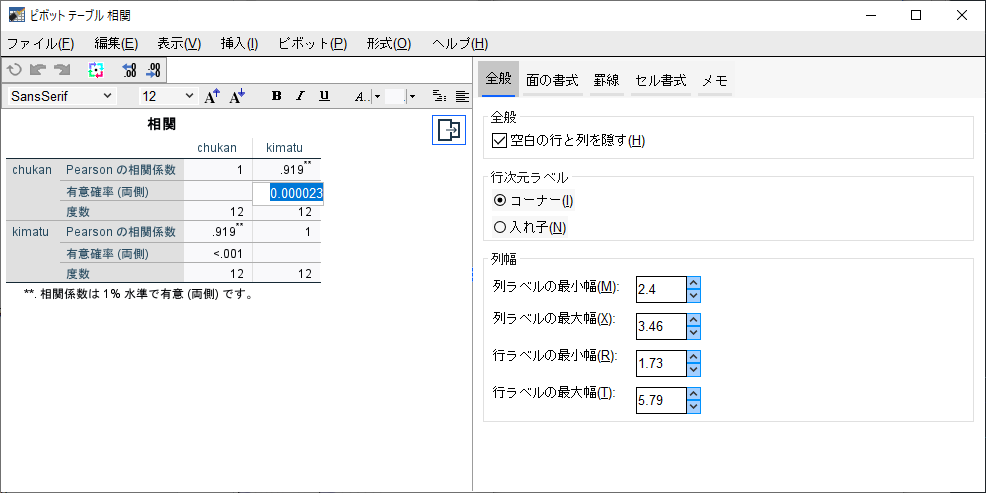
表をダブルクリックして、相関係数をダブルクリックすると、0.919416であることがわかる。
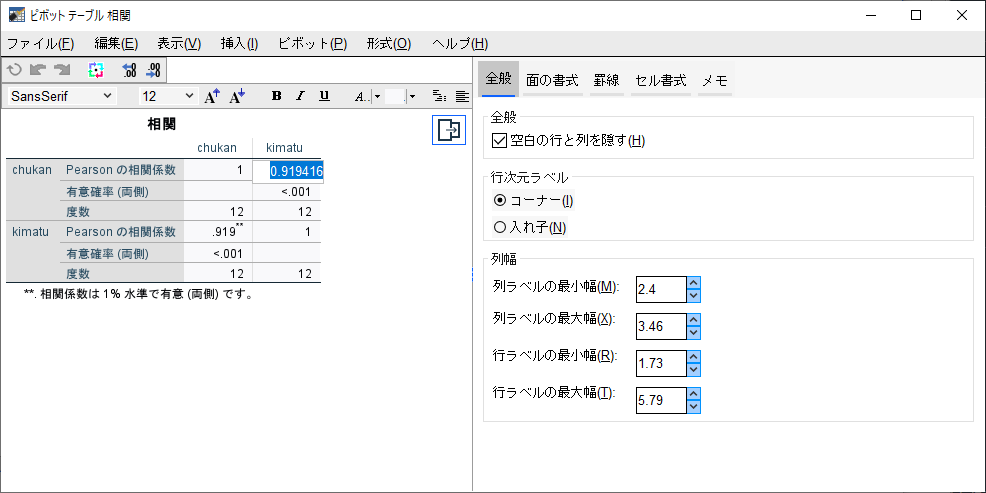
p値は、0.000023であることがわかる。
ともに、四捨五入の違いだけで、Excelでの計算結果と同じと言える。
ペア数の計算は、「分析」→「検定力分析」→「相関」→「Pearsonの積率」を選択。
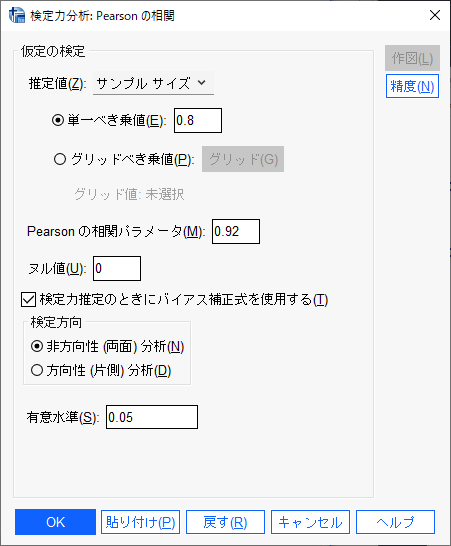
検出力(単一べき乗値とある枠)に0.8、Pearsonの相関パラメータに0.92を入れて、有意水準を0.05のままにして、OKをクリックする。
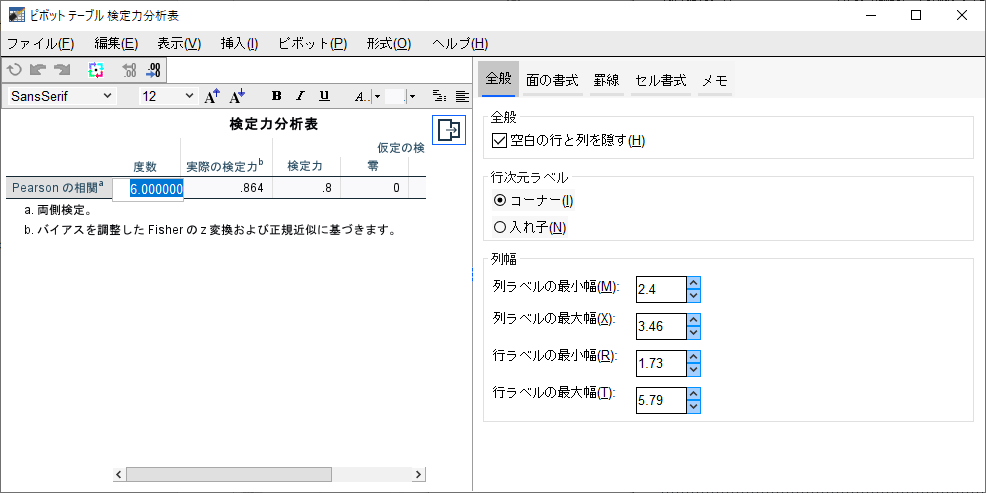
度数は6と計算される。

Excelシートでも6.108459であって、切り上げて7としているので、およそ間違いないと言える。
SPSSは詳細を見ても6.000となっていて、正確なところは謎のままである。
まとめ
相関係数の計算、検定、サンプル数計算をR、EZR、エクセル、SPSSで実施した。
参考になれば幸い。
関連記事










コメント
コメント一覧 (1件)
[…] […]