積極的に同等であることを証明していく同等性の検定。
サンプルサイズ計算はどのようにすればよいか?
同等性検定はどのようにするのか?
同等性の検定は、簡単に言えば、非劣性検定の群を入れ替えて、片側検定を2回行うことで実施できる。
劣っていないが、優れてもいない、というのが同等の定義になる。
ただし、どのくらいの差が臨床的に意味のある差(同等と言える限界)であるかが難しい。
非劣性検定の詳細はこちら。

同等性検定のサンプルサイズ計算はどのようにするのか?
平均値の場合
平均値の同等性検定のサンプルサイズ計算はどのようにすればよいか?
一群のサンプルサイズは以下の式で計算できる。
$$ n = 2 \left( \frac{Z_{\alpha/2} + Z_{\beta/2}}{\Delta/\sigma} \right)^2 $$
Δは、臨床的に意味がある差。
σは、2群共通の標準偏差。
α、β は、それぞれ第1種と第2種の過誤。
いわゆるαエラーとβエラー。
2群の母集団の差はゼロと考えている。
Rのスクリプトは以下の通り。
sample.size.equivalence.mean <- function
(sig.level=.05, power=.8,Delta=0, Delta1, sd=1, alternative="two.sided"){
alternative <- match.arg(alternative)
tside <- switch(alternative, one.sided=1, two.sided=2)
# sample size calculation
d <- (Delta + Delta1)/sd
Za <- qnorm(sig.level/tside, lower.tail=FALSE)
Zb <- qnorm(1-(1-power)/2)
n <- 2*((Za+Zb)/d)^2
# output
NOTE <- "n is number in *each* group"
METHOD <- "Equivalence Test Sample Size (Mean)"
structure(list(n = n, "Sample Diff" = Delta,
"Clin.Sig.Diff"=Delta1, SD = sd, sig.level = sig.level,
power = power, alternative = alternative, note = NOTE,
method = METHOD), class = "power.htest")
}
2つ例題を実行してみる。
標準偏差 1 に対して、臨床的に意味のある差が0.5の時と、0.1の時を計算してみた。
0.5は現実的だが、0.1は非現実的な数字になる。
> sample.size.equivalence.mean(power=0.8, Delta1=0.5)
Equivalence Test Sample Size (Mean)
n = 84.05938
Sample Diff = 0
Clin.Sig.Diff = 0.5
SD = 1
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group
> sample.size.equivalence.mean(power=0.8, Delta1=0.1)
Equivalence Test Sample Size (Mean)
n = 2101.485
Sample Diff = 0
Clin.Sig.Diff = 0.1
SD = 1
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group
EZRで計算すると以下の通りになる。
ポイントはβエラーを半分にするところ。
検出力80%の場合、βエラーは20%。
その半分の10%を100%から引いて、90%。
この90%の小数、0.9を検出力に入力する。
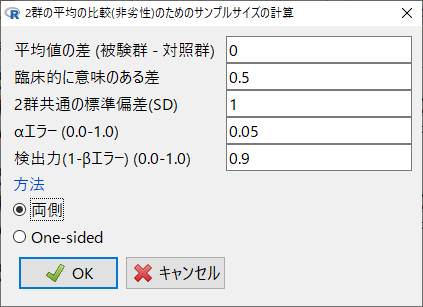
結果は上記と同じになる。必要症例数は切り上げるので、R functionでの結果と同じだ。

非現実的な設定も、同じ数字になった。

比率の場合
比率(割合)の場合は、かなり複雑なので式は割愛。
詳しく知りたい人は参考書籍をどうぞ。

Rスクリプトは以下の通り。
2群の割合、pAとpBは同じ値にする。
βエラーが半分になっているのは、平均値の時と同じ。
sample.size.equivalence.prop.likelihood <- function
(pA, pB, DELTA, power=.8, sig.level=.05, alternative="two.sided"){
alternative <- match.arg(alternative)
tside <- switch(alternative, one.sided = 1, two.sided = 2)
#sample size calculation
delta <- pA-pB
a <- 2
b <- -2*pB-2-3*DELTA-delta
c <- DELTA^2+2*(1+pB)*DELTA+2*pB+delta
d <- -pB*DELTA*(1+DELTA)
v <- b^3/(27*a^3)-(b*c)/(6*a^2)+d/(2*a)
u <- sign(v)*sqrt(b^2/(9*a^2)-c/(3*a))
w <- (pi+acos(v/u^3))/3
pB.star <- 2*u*cos(w)-b/(3*a)
R <- sqrt((pB.star-DELTA)*(1-pB.star+DELTA)+pB.star*(1-pB.star))
S <- sqrt(pA*(1-pA)+pB*(1-pB))
Za <- qnorm(sig.level/tside, lower.tail=FALSE)
Zb <- qnorm(1-(1-power)/2)
n <- ((Za*R+Zb*S)/(delta+DELTA))^2
#output
NOTE <- "n is number in *each* group"
METHOD <- "Equivalence Test Sample Size (Likelihood Method)"
structure(list(n = n, pA = pA, pB = pB, "Clin.Sig.Diff"=DELTA,
sig.level = sig.level, power = power, alternative = alternative, note = NOTE,
method = METHOD), class = "power.htest")
}
2群ともにエンドポイントの割合が0.5として、臨床的に意味のある差を0.05, 0.1とすると計算結果は以下の通りとなる。
いずれにしても大変大きなサンプルサイズが必要になる。
> sample.size.equivalence.prop.likelihood(pA=0.5, pB=0.5, DELTA=0.05)
Equivalence Test Sample Size (Likelihood Method)
n = 2098.307
pA = 0.5
pB = 0.5
Clin.Sig.Diff = 0.05
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group
> sample.size.equivalence.prop.likelihood(pA=0.5, pB=0.5, DELTA=0.10)
Equivalence Test Sample Size (Likelihood Method)
n = 522.1914
pA = 0.5
pB = 0.5
Clin.Sig.Diff = 0.1
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group
EZRでもやってみる。
平均値の時と同じく非劣性のサンプルサイズメニューを借りる。
臨床的に意味のある差を0.05とした場合は、以下のようにセットする。
検出力は全体で80%であるが、片側検定を2回行う都合で、βエラーを半分にして90%とする。
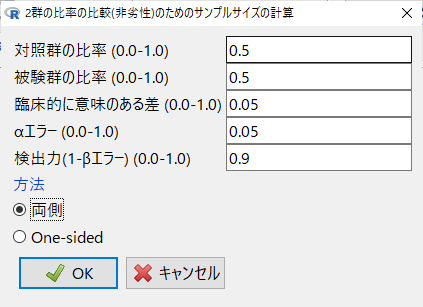
結果は、上記のスクリプトの結果と同様の結果になる。

臨床的に意味のある差を0.1としても同様の結果になる。

まとめ
同等性検定のサンプルサイズ計算を紹介した。
参考になれば。
参考書籍

おすすめ書籍








コメント