分散分析のサンプルサイズ計算をSPSSで行う方法
分散分析のサンプルサイズをSPSSで計算する前に効果量を見積もる
分散分析のサンプルサイズをSPSSで計算する際に、必要なのは効果量を見積もること
先行研究の分散分析表を使うとよい
今回は tension の高さによって warpbreak の数が異なるかどうかのデータを用いて、先行研究の分散分析表をどのように活用すればよいかを解説する
まず、サンプルデータは以下のように集計されるデータである
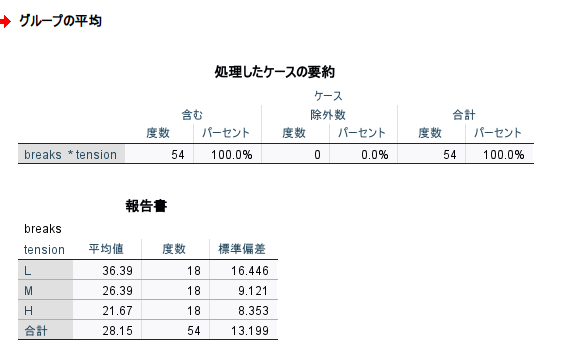
各群 18 例で、合計 54 例
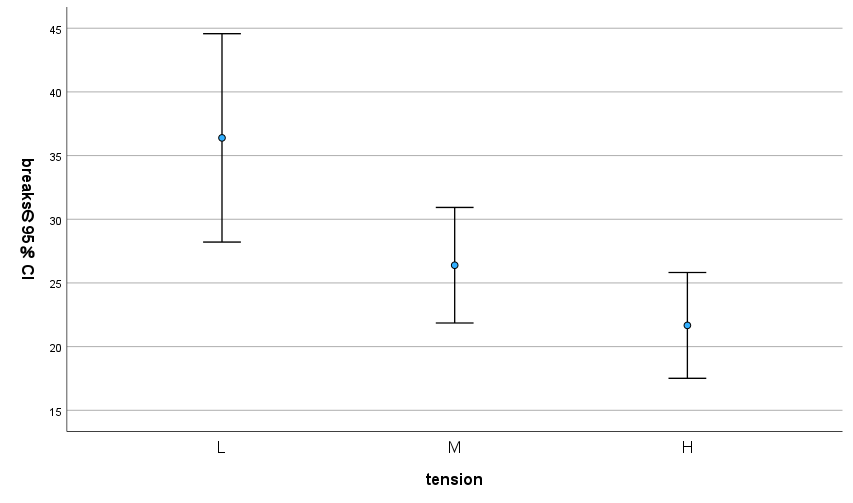
各群の warpbreak の平均値をグラフにすると、上記のようになり差がありそうなことがわかる
このとき分散分析表は以下のように計算される
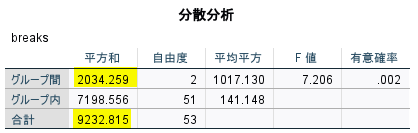
この分散分析表から効果量を見積もるには、グループ間の平方和と合計の平方和に着目する
グループ間の平方和を合計の平方和で割った値がイータの 2 乗である
$$ \displaystyle \begin{equation} \eta^2 = \frac{2034.259}{9232.815} \fallingdotseq 0.220 \end{equation} $$
イータの 2 乗は約 0.220 と計算される
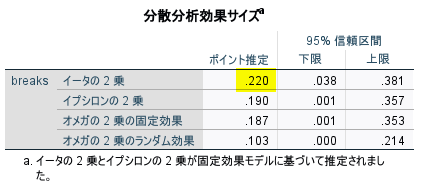
このイータの 2 乗を使って、以下のように効果量 f が計算される
$$ \displaystyle \begin{equation} f = \sqrt{\frac{\eta^2}{1-\eta^2}} = \sqrt{\frac{0.22}{1-0.22}} \fallingdotseq 0.53 \end{equation} $$
効果量 f は、約 0.53 と計算される
分散分析のサンプルサイズ計算をSPSSで行う具体的な方法
分散分析のサンプルサイズ計算をSPSSで行う具体的な方法を解説する
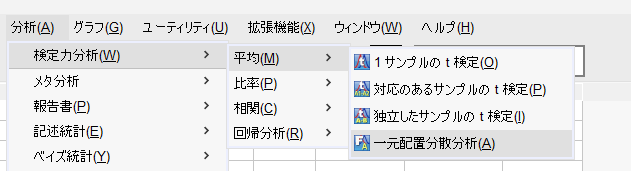
「分析」→「検定力分析」→「平均」→「一元配置分散分析」のメニューを開く
単一べき乗値(検出力)に 0.8 を入力する
検証的試験の場合は 0.9 にすることもある
指定:というところを変更する
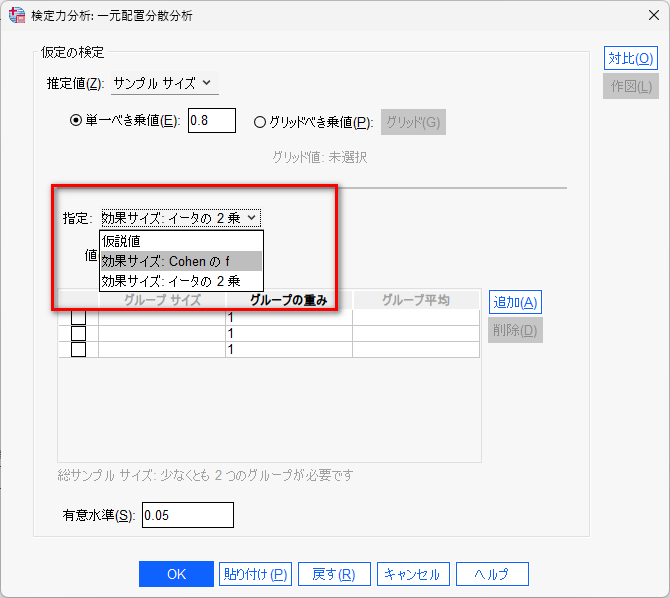
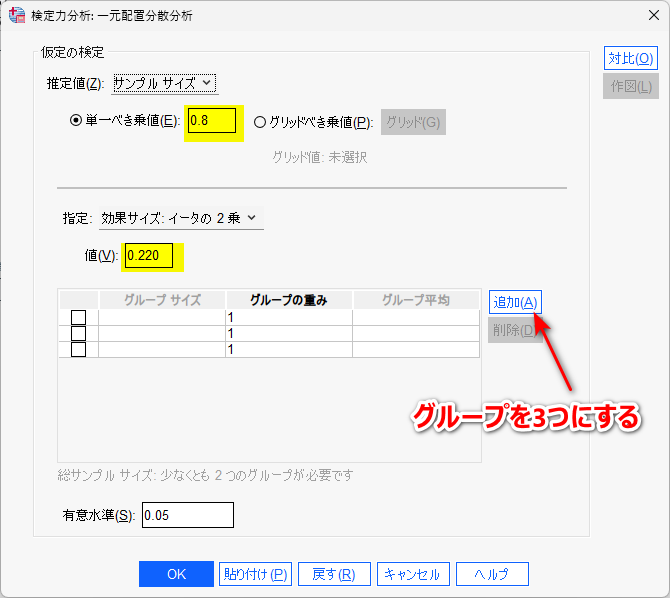
効果サイズ:イータの 2 乗を選択し、値枠に 0.220 を入力する
Warpbreaks のデータでは、tension の種類が 3 つであったため、「追加」をクリックしグループを 3 つにする
OK をクリックすると必要なサンプルサイズが計算される

1 群 13 例必要と計算された
実際は 18 例であったので、十分なサンプルサイズであったと言える
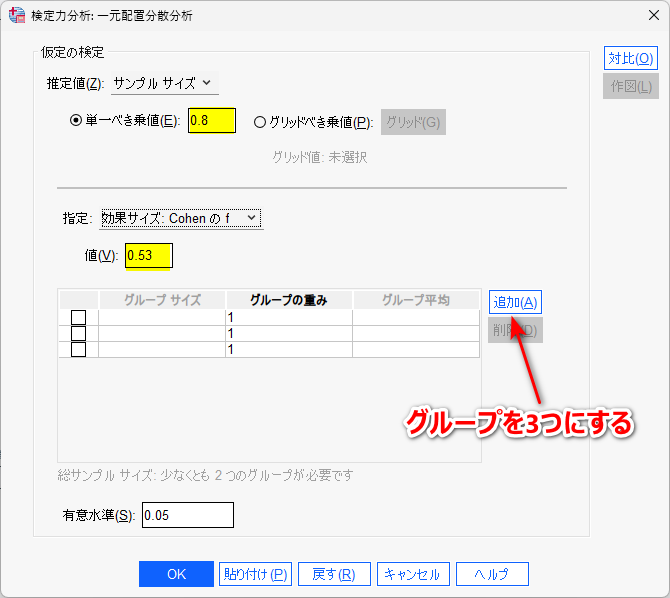
効果サイズ: Cohen の f として再度計算してみる
指定:を Cohen の f に変更して、値枠に 0.53 を入力する
OK をクリックすると必要なサンプルサイズが計算される
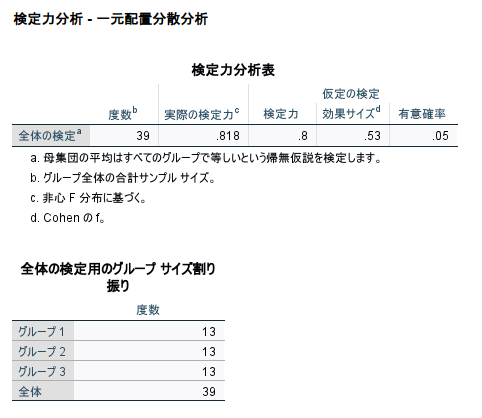
先ほどと同じように 1 群 13 例必要と計算された
まとめ
分散分析のサンプルサイズ計算を SPSS で行いたい場合、まず先行研究の分散分析表を入手する必要がある
グループ間の平方和と合計の平方和の比イータ 2 乗か、イータ 2 乗から計算される効果量 f を計算する必要がある
イータ 2 乗もしくは効果量 f が計算できれば、あとは簡単に必要サンプルサイズが計算できる
参考書籍
Jacob Cohen. Statistical power analysis for the behavioral sciences. Second edition.








コメント