ROC曲線分析をしたいが、何人のデータを集めたらいいかわからない。
こんなときどうするか?
ROC 曲線分析に必要なサンプル数の計算を R で行う準備
まずpROCパッケージをインストールする。
インストールは一回でOK。
install.packages("pROC")
毎回呼び出しのためlibrary()を実施。
library(pROC)
ROC 曲線分析に必要なサンプル数を計算するのに必要な数値
ROC曲線分析のサンプルサイズ計算に必要な数値は、AUC (Area Under the Curve) の見積もり値と、検出力だ。
AUCが0.5の時に、凸なしで、対角線のようになる。
この場合は、検査として役に立たない。
AUCは、0.5よりも大きいことが大前提で、仮説検定は帰無仮説は0.5以下、対立仮説は0.5超とするのが妥当なため、片側検定が望ましい。
以下も参照。
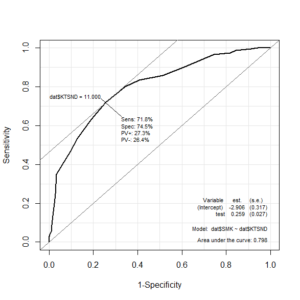
たとえば、AUCが0.8、検出力0.90、有意水準5%、片側検定、疾患あり、なしが1:1とする。
- AUC=0.80
- power=0.90
- Significant level=0.05
- ratio of normal to abnormal = 1:1
- one-sided test
このとき以下のようなスクリプトを書く。
power.roc.test(auc=0.80, power=0.90, alternative="one")
結果として、疾患ありもなしも、13.38553切り上げて14例ずつと計算される。
> power.roc.test(auc=0.80, power=0.90, alternative="one")
One ROC curve power calculation
ncases = 13.38553
ncontrols = 13.38553
auc = 0.8
sig.level = 0.05
power = 0.9
疾患なしが2、疾患ありが1とすると、21例と11例がそれぞれ必要と計算され、合計32例が必要となる。
疾患なし:ありの比はkappa=という変数で指定する。
> power.roc.test(auc=0.8, power=0.9, alternative="one", kappa=2)
One ROC curve power calculation
ncases = 10.34798
ncontrols = 20.69596
auc = 0.8
sig.level = 0.05
power = 0.9
ROC 曲線分析のサンプル数計算に必要な AUC と検出力はどう決めるか
特に決まりはない。
研究者が良かれと思う基準で決めるしかない。
先行研究がある場合は大いに参考になる。
AUCが1に近いと予想される場合、必要なサンプルサイズは小さくなる。
以下に、上記の条件(AUC = 0.8, 検出力 = 0.9 で、疾患あり・なしともに 14 例ずつ必要)から、AUC や検出力を変えると、必要サンプル数はどのように変わるかを示す。
AUCを 0.8 から 0.9 にすると、14例ずつだったものが、7例ずつになる。
> power.roc.test(auc=0.90, power=0.90, alternative="one")
One ROC curve power calculation
ncases = 6.124355
ncontrols = 6.124355
auc = 0.9
sig.level = 0.05
power = 0.9
power.roc.test() の作成者は、患者でも対照でも、必要サンプルサイズが10例を下回ったら、最低でも10例サンプリングするのが望ましいと勧めている。
AUCが0.5に近いと予想すると、必要なサンプルサイズは大きくなる。
AUCを 0.8 から 0.6にすると、14例ずつだったものが、135例ずつになる。
> power.roc.test(auc=0.60, power=0.90, alternative="one")
One ROC curve power calculation
ncases = 134.638
ncontrols = 134.638
auc = 0.6
sig.level = 0.05
power = 0.9検出力を下げると必要なサンプルサイズは小さくなる。
検出力を0.9 から 0.8 に下げると、14例ずつだったものが、10例ずつになる。
> power.roc.test(auc=0.80, power=0.80, alternative="one")
One ROC curve power calculation
ncases = 9.933712
ncontrols = 9.933712
auc = 0.8
sig.level = 0.05
power = 0.8
検出力を上げると必要なサンプルサイズは大きくなる。
検出力を 0.9 から 0.95に上げると、14例ずつだったものが、17例ずつに変わる。
> power.roc.test(auc=0.80, power=0.95, alternative="one")
One ROC curve power calculation
ncases = 16.62344
ncontrols = 16.62344
auc = 0.8
sig.level = 0.05
power = 0.95
ROC 曲線分析に必要なサンプル数の計算を自前 R スクリプトで行う
power.roc.test 関数を使わず、参考文献にある計算式を R スクリプトに起こして、以下のような自前関数を作った
sample.size.one.roc <- function(auc, sig.level=.05, power=.8,
alternative="one.sided",
cpratio=1){
alternative <- match.arg(alternative)
tside <- switch(alternative, one.sided=1, two.sided=2)
A <- qnorm(auc) * 1.414
V <- (0.0099*exp(-1*A^2/2)*((5*A^2+8)+(A^2+8)/cpratio))
Za <- qnorm(sig.level/tside, lower.tail=FALSE)
Zb <- qnorm(power)
nD <- (Za*sqrt(0.0792*(1+1/cpratio))+Zb*sqrt(V))^2 / (auc-0.5)^2
nC <- nD*cpratio
METHOD <- "One ROC curve sample size calculation"
structure(list(ncases=nD, ncontrols=nC, auc=auc,
sig.level=sig.level, power=power,
alternative=alternative,
Cont.Pts.ratio=cpratio, method=METHOD),
class="power.htest")
}
以下のように auc, power, cpratio(対照・患者比)を指定すると、上記と同じ計算結果が得られるので、興味あれば試してみてほしい
sample.size.one.roc(auc=0.8, power=0.9)
sample.size.one.roc(auc=0.8, power=0.9, cpratio=2)
sample.size.one.roc(auc=0.9, power=0.9)
sample.size.one.roc(auc=0.6, power=0.9)
sample.size.one.roc(auc=0.8, power=0.8)
sample.size.one.roc(auc=0.8, power=0.95)ROC 曲線分析に必要なサンプル数の計算をエクセルで行う
上記の計算をエクセルでも行えるようにした。
よければ。
ROC曲線のためのサンプルサイズ計算【エクセルでサンプルサイズ】 | TKER SHOP
以下は、使い方動画。
ROC 曲線分析に必要なサンプル数の計算をアプリで行う
デスクトップアプリはこちら
引用文献情報
pROC パッケージの引用文献情報は、以下のとおり
Xavier Robin, Natacha Turck, Alexandre Hainard, Natalia Tiberti,
Frédérique Lisacek, Jean-Charles Sanchez and Markus Müller (2011).
pROC: an open-source package for R and S+ to analyze and compare ROC
curves. BMC Bioinformatics, 12, p. 77. DOI: 10.1186/1471-2105-12-77
<http://www.biomedcentral.com/1471-2105/12/77/>
エクセルファイルの引用文献は、以下の論文である
ROC curves in clinical chemistry: uses, misuses, and possible solutions
まとめ
ROC曲線分析のサンプルサイズ計算を R で行う方法を紹介した。
pROCパッケージを使って計算できる。
エクセルでも計算できるようにした。
予想 AUC と検出力をどうするかを、先行研究を踏まえて決めておく必要がある。
参考文献
ROC curves in clinical chemistry: uses, misuses, and possible solutions








コメント
コメント一覧 (1件)
[…] R で ROC 曲線分析に必要なサンプル数を計算する方法 ROC曲線分析をしたいが、何人のデータを集めたらいいかわからない。 […]