お互いにある変数と相関がある変数同士の相関係数を算出する場合、お互いに相関がある変数の影響を排除したうえでの相関を検討したいことがある。
そのようなときに使う方法が偏相関係数だ。
偏相関係数を算出する試験デザインを考える際に、サンプルサイズ計算はどのようにすればいいのか?
偏相関係数とは?
偏相関係数とは、お互いにある変数と相関がある変数同士の相関係数を考える際に、お互いに相関がある変数の影響を排除した相関係数のこと。
偏相関係数については、こちらが詳しい。
偏相関係数のサンプルサイズ計算はどうやる?
偏相関係数のサンプルサイズ計算プログラムは、簡単には利用可能ではない。
統計ソフトRでは利用できるプログラムは見つからなかったが、SPSSでは利用可能だ。
偏相関係数のサンプルサイズ計算をSPSSで行う方法
まず相関係数のサンプルサイズ計算をしてみる
SPSSのメニューから「分析」→「検定力分析」→「相関」→「Pearsonの積率」の順に選んでいく。
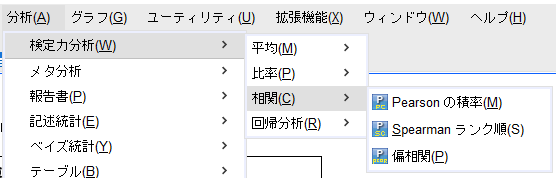
例えば、検出力80%、検出したい相関係数を0.5、検定は両側で有意水準5%とする。
ここで「単一べき乗値」という言葉あるが、single power value(一つの検出力の値)のことと思われる。
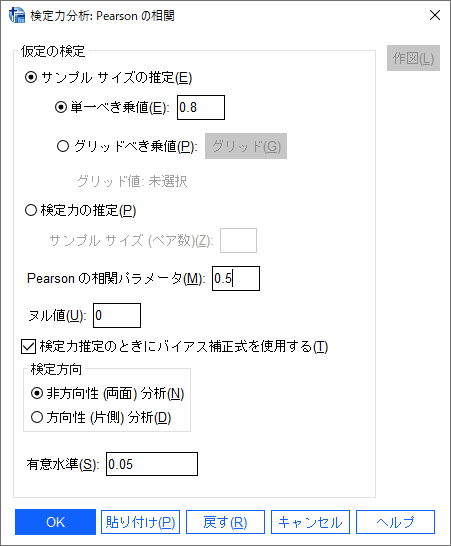
結果は、29例必要と計算される。

一つの変数の影響を除いた偏相関係数の計算をしてみる
SPSSのメニューから「分析」→「検定力分析」→「相関」→「偏相関」の順に選んでいく。
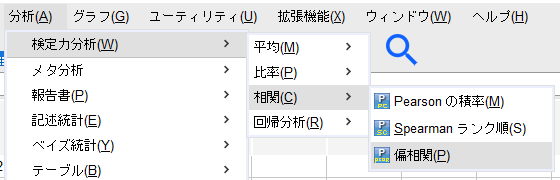
例えば、検出力80%、影響を除く変数を1つ、検出したい偏相関係数を0.5、検定は両側で有意水準5%とする。
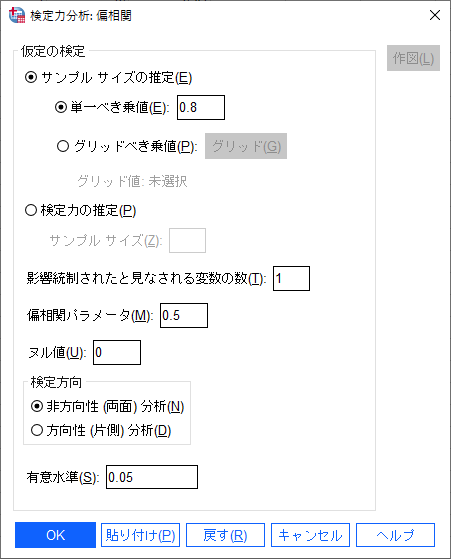
結果は、30例必要と計算される。

影響を除く変数を増やしてみる
影響を除く変数を2つにすると、必要なサンプルサイズは31例と計算される。

影響を除く変数を3つにすると、必要なサンプルサイズは32例と計算される。

影響を除く変数1つにつき、必要な例数は1ずつ増えるという規則になっている。
検出したい偏相関係数や検出力を変えても同様に、制御変数1つ増加に対して1例ずつ必要例数が増えていく。
まとめ
相関係数を計算したいとき、2つの変数がともに相関がある変数の影響を排除することができるのが偏相関係数だ。
偏相関係数のサンプルサイズ計算はSPSSでできる。
上記のように試した結果や、下記の参考文献の記載を確認すると、単純な相関係数のためのサンプルサイズに、影響を除く変数の数だけ足すことで問題ないと考えられる。
参考文献
Algina, James & Olejnik, S.F.. (2003). Sample Size Tables for Correlation Analysis with Applications in Partial Correlation and Multiple Regression Analysis. Multivariate Behavioral Research. 38. 309-323. 10.1207/S15327906mbr3803_02.
https://www.tandfonline.com/doi/abs/10.1207/S15327906MBR3803_02
上記文献中P.316に下記の記載があり、単純な相関係数のためのサンプルサイズに、調整する変数の数だけ足すことで問題ないと理解できる。
… suppose a researcher believes that the population partial correlation coefficient, with four variables controlled, is .30 and wants ±.15 accuracy. The relevant entry in Table 1 is 143. Adding four, the required sample size would be 147.








コメント