構造方程式モデリングを ざっくり わかりやすく 解説

構造方程式モデリング（SEM）とは？

ざっくり、わかりやすく解説

構造方程式モデリング SEMとは？

構造方程式モデリングは、英語の略語で SEMと呼ばれ、Structural Equation Modeling の略である。

これは複数の変数を用いて、理屈で考えた、変数間の相関や因果関係、因子構造の当てはまりを確認しながら、概念構造を明らかにする解析方法である。

これによって、複雑に絡み合った多数の観測値同士の構造を明らかにすることができ、複雑な現実問題を読み解く手掛かりになる。

厳密には異なるかもしれないが、個人的には、共分散構造方程式も、パス解析もすべてひっくるめて考えればよいと思っている。

パス解析は潜在変数を用いない方法という定義かなと思うが、パス解析も SEM のソフトウェアで解析できるので、一緒のグループと考えて良いと思う。

SEMができるソフトウェアは？

有料なものでは、Amos（エイモス）が有名である。IBM SPSS から提供されている。

グラフィックを描いて解析するので、図の描き方に慣れてしまえば、直感的でとっつきやすい。

だが、M-plusというソフトウェアがもっとも優れているようである。

以下は、参考書籍。

コマンドを指定して解析するため、慣れが必要と思う。

（一部はDiagrammerという機能を使ってパス図で解析できる。）

R と似たような感じと思う。

無料のものでは、R の lavaan パッケージ。

これも R スクリプトと呼ばれるコマンドを書く必要があるため慣れるまで少し大変だが、無料という点が優れている。

SEMのパス図の例

Amosが圧倒的に使いやすいがその理由はグラフィックで構造を指定する点が挙げられる。

図はやはり直感的でわかりやすい。

以下の例は、楕円の潜在変数（観測されたデータから計算上推定されたデータ）と、長方形の観測変数（実際に測定して得られたデータ）を用いたパス図である。

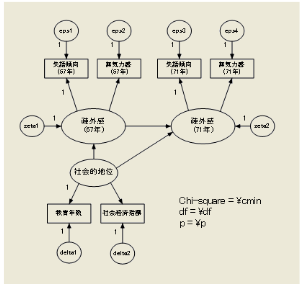
出典：IBM SPSS Amos 28 ユーザーズ ガイド

https://www.ibm.com/docs/en/SSLVMB_28.0.0/pdf/amos/IBM_SPSS_Amos_User_Guide_ja.pdf

パス図は、変数同士の関係性を示した経路の図のことである。

一方向矢印が、その方向へ説明するという意味で、両矢印は相関関係という意味である。

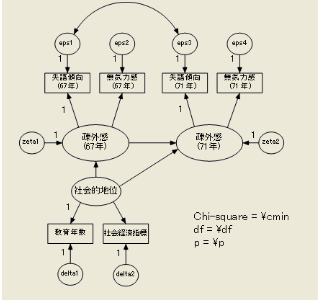
矢印は、回帰分析や因子分析、主成分分析を意味していて、両矢印は相関分析を意味していると考えれば良い。

矢印の先には、必ず誤差を表す丸で示した変数がついている。

M-plus（一部は使用可能）や R の lavaan はこのような図は使わないが、このような図をイメージしながら、モデル式を書いていくことになる。

SEMの利点

多数の変数同士の関係性を探索的に検討していくことで、潜在的な概念や関係性を見出すことができる点で、とても興味深い分析手法だ。

個々に回帰分析、因子分析、主成分分析を繰り返すのとは違い、理論的に考えたモデルとして、回帰分析や主成分分析の組み合わせ、因子分析の潜在変数間の相関や回帰などを、同時に扱うことができる。

観測された多数の変数を使って、潜在的な変数を推測しながら、現実の複雑性を理解していくという方法で、複雑な世の中を複雑なまま理解しようとする手法と言える。

SEMの注意点

SEMの注意点は２つ考えられる。

1. 計算が収束しないことがあること。
2. あてはまりが悪い場合は、計算できていても、適切とは言えないということ。

１つ目の計算が収束しないということは、つまりは、計算結果が出力されないということがあるという意味である。

理論的に考えたモデルがそもそも計算できないものだったり、観測データとモデルとが適合していなかったり、理由はさまざまである。

計算されない場合は、計算される単純なモデルに戻してみる・分解してみるなど、試行錯誤を繰り返す必要がある。

２つ目は、あてはまりの問題である。

あてはまりにはいくつかの指標があり、その指標でチェックする。

あてはまりの指標が、あまりよくない結果ということは、計算結果は出ていても、想定したモデルにあてはまっているとは言えないということなので、理屈で考えたモデルを、観測したデータで説明したことにはならないということだ。

なので、そのモデルが正しいことを支持する傍証を得たことにならないということなのだ。

このような注意点がある。

まとめ

構造方程式モデリング SEM Structural Equation Modeling とは、回帰分析、因子分析、主成分分析、相関分析等を組み合わせた、ある特定の概念体系を説明するような理論的なモデルを、観測したデータで説明できるかどうか確認する、解析方法である。

多数の変数をさまざまな解析方法で同時に扱える利点がある一方で、計算が収束しない問題や、モデルへのあてはまりがあまりよくないことが往々にして起こる問題に対して、試行錯誤をしていかねばならない困難がある。

探索的な解析は、困難と同時に、さまざまな工夫によるワクワクと、うまく行ったときの達成感が味わえる。

事実、試行錯誤の末、モデルが収束して計算結果が出力されたときの達成感はこの上ない。

参考になれば。

参考書籍

M-plusとRによる構造方程式モデリング入門