R で回帰直線の差の検定を行う方法

二つのデータセットがあって、二つの回帰直線が描けたとき、そのあとどうすればいいか？

そのあとは、傾きが同じと言えるか？さらには切片が同じと言えるか？と進んでいく。

二つの回帰直線の差を検定してみる。

回帰直線の差の検定のためのサンプルデータ

データはこちら。C地区とO地区のNO2濃度（X）とせき・たん有症割合（Y）のデータ。

NO2.c <- c(0.025,0.030,0.016,0.028,0.021,0.041,0.012,0.015,0.030,0.018,0.023)
pre.c <- c(4.1,6.8,2.6,11.5,2.8,10.7,2.7,2.8,3.5,5.0,3.6)
are.c <- rep("c",length(NO2.c))
NO2.o <- c(0.024,0.033,0.030,0.017,0.022,0.027,0.016,0.017,0.020,0.022)
pre.o <- c(6.8,8.7,11.4,4.5,5.6,10.5,5.2,6.8,6.0,8.0)
are.o <- rep("o",length(NO2.o))

回帰直線の差の検定の前にまず散布図を描いてみる

散布図を描くにはplot()を使う。

O地区は、points()を使って、三角（pch=2）でプロットしている。

plot(NO2.c, pre.c, las=1, xlim=c(0,0.05), ylim=c(0,12),
xlab="Annual average of NO2 concentration",
ylab="Prevalence of cough and/or sputum (%)")
title(" Difference between two regression lines ")
points(NO2.o, pre.o, pch=2)

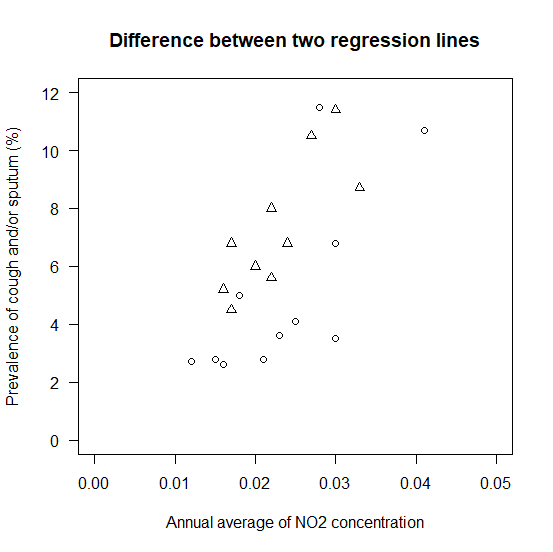
回帰直線を求めてみる

function(){} で自作した関数で回帰直線の傾きと切片を求める。

linear.reg <- function(x,y){
xbar <- mean(x)
ybar <- mean(y)
n <- length(x)
b <- sum((x-xbar)*(y-ybar))/sum((x-xbar)^2)
a <- ybar-b*xbar
yhat <- a+b*x
R2 <- sum((yhat-ybar)^2)/sum((y-ybar)^2)
VE <- 1/(n-2)*sum((y-(a+b*x))^2)
rse <- sqrt(VE)
SEb <- sqrt(VE/sum((x-xbar)^2))
Tb <- b/SEb
pb <- 2*pt(abs(Tb), n-2, lower.tail=F)
bl <- b-qt(1-0.05/2, n-2)*SEb
bu <- b+qt(1-0.05/2, n-2)*SEb
SEa <- sqrt(VE*(1/n+xbar^2/sum((x-xbar)^2)))
Ta <- a/SEa
pa <- 2*pt(abs(Ta), n-2, lower.tail=F)
al <- a-qt(1-0.05/2, n-2)*SEa
au <- a+qt(1-0.05/2, n-2)*SEa
list(
c(Slope=b,"t_Slope"=Tb, "p_Slope"=pb, "LL_Slope"=bl, "UL_Slope"=bu,
Intercept=a,"t_Intcp"=Ta, "p_Intcp"=pa, "LL_Intcp"=al, "UL_Intcp"=au,
"Error Var."=VE,"Resid. SE"=rse,"R^2"=R2))
}
linear.reg(x=NO2.c, y=pre.c)
linear.reg(x=NO2.o, y=pre.o)
linreg.c <- unlist(linear.reg(x=NO2.c, y=pre.c))
linreg.o <- unlist(linear.reg(x=NO2.o, y=pre.o))

結果はこちら。

> linear.reg(x=NO2.c, y=pre.c)
[[1]]
Slope      t_Slope      p_Slope     LL_Slope     UL_Slope
279.85418266   3.23205342   0.01028875  83.98051896 475.72784635
Intercept      t_Intcp      p_Intcp     LL_Intcp     UL_Intcp
-1.48929394  -0.69132430   0.50680073  -6.36257401   3.38398613
Error Var.    Resid. SE          R^2
5.32855590   2.30836650   0.53718391
> linear.reg(x=NO2.o, y=pre.o)
[[1]]
Slope       t_Slope       p_Slope      LL_Slope      UL_Slope
317.540322581   3.780409062   0.005385004 123.844538638 511.236106524
Intercept       t_Intcp       p_Intcp      LL_Intcp      UL_Intcp
0.110080645   0.055902022   0.956790802  -4.430835999   4.650997290
Error Var.     Resid. SE           R^2
2.099679940   1.449027239   0.641118694

C 地区と O 地区ごとに、Slope（傾き）と Intercept（切片）が計算され、検定や信頼区間推定の数値や、R 2 乗が計算されている

回帰直線を描き入れてみる

先ほどの散布図に二つの回帰直線を描き入れてみる。

Ｃ地区が実線で、Ｏ地区が点線（lty=2）だ。

abline(a=linreg.c[6], b=linreg.c[1])
abline(a=linreg.o[6], b=linreg.o[1], lty=2)

描き入れた図はこちら。

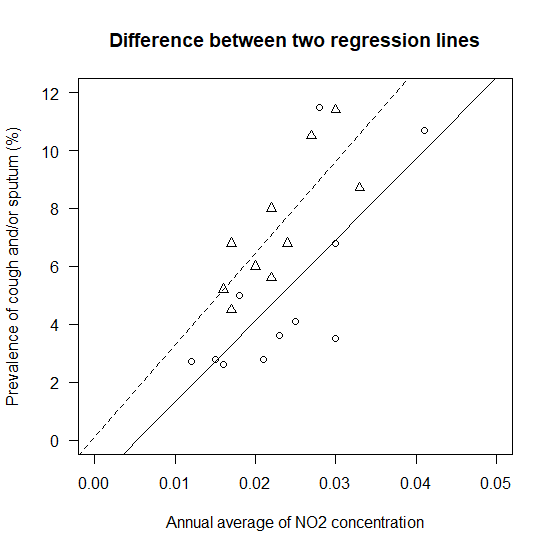
回帰直線の差の検定（傾きが同じかどうか）

上の図を見ると、二つの回帰直線の傾きはとても近いが、同じにして話を進めてもいいかどうかの検定。

Rのスクリプトは以下の通り。

reg.line.diff <- function(X1, Y1, X2, Y2){
X <- c(X1,X2)
Y <- c(Y1,Y2)
X1bar <- mean(X1)
X2bar <- mean(X2)
Xbar  <- mean(X)
Y1bar <- mean(Y1)
Y2bar <- mean(Y2)
Ybar  <- mean(Y)
SSXY1 <- sum((X1-X1bar)*(Y1-Y1bar))
SSXY2 <- sum((X2-X2bar)*(Y2-Y2bar))
SSXY  <- sum((X-Xbar)*(Y-Ybar))
SSX1  <- sum((X1-X1bar)^2)
SSX2  <- sum((X2-X2bar)^2)
SSX   <- sum((X-Xbar)^2)
SSY1  <- sum((Y1-Y1bar)^2)
SSY2  <- sum((Y2-Y2bar)^2)
SSY   <- sum((Y-Ybar)^2)
Delta1 <- SSY1-(SSXY1)^2/SSX1 + SSY2-(SSXY2)^2/SSX2
Delta2 <- SSY1+SSY2 - (SSXY1+SSXY2)^2/(SSX1+SSX2)
n <- length(X1)
m <- length(X2)
N  <- n+m
Fb <- (Delta2-Delta1)/(Delta1/(N-4))
pb <- pf(Fb, 1, N-4, lower.tail=F)
b1 <- SSXY1/SSX1
b2 <- SSXY2/SSX2
a1 <- Y1bar-b1*X1bar
a2 <- Y2bar-b2*X2bar
bE <- (SSXY1+SSXY2)/(SSX1+SSX2)
Delta3 <- SSY-(SSXY)^2/SSX
Fa <- (Delta3-Delta2)/(Delta2/(N-3))
pa <- pf(Fa, 1, N-3, lower.tail=F)
aE1 <- Y1bar-bE*X1bar
aE2 <- Y2bar-bE*X2bar
bT <- SSXY/SSX
aT <- Ybar-bT*Xbar
a.diff <- aE2-aE1
a.diff.l <- a.diff-qt(1-0.05/2, N-3)*sqrt((1/n+1/m+(X1bar-X2bar)^2/(SSX1+SSX2))*(Delta2/(N-3)))
a.diff.u <- a.diff+qt(1-0.05/2, N-3)*sqrt((1/n+1/m+(X1bar-X2bar)^2/(SSX1+SSX2))*(Delta2/(N-3)))
conf <- qt(1-0.05/2, N-3)*sqrt((1/n+1/m+(X1bar-X2bar)^2/(SSX1+SSX2))*(Delta2/(N-3)))
list(c(Delta1=Delta1, Delta2=Delta2, F_Slopes=Fb, p_Slopes=pb,
Delta3=Delta3, F_Intcps=Fa, p_Intcps=pa,
Slope1=b1, Slope2=b2, Intcp1=a1, Intcp2=a2,
Slope_Common=bE, Intcp1_Slope_Common=aE1, Intcp2_Slope_Common=aE2,
Diff_Intcps=a.diff, Diff_Intcps_LL=a.diff.l, Diff_Intcps_UL=a.diff.u,
Slop_Total=bT, Intcp_Total=aT))
}
reg.line.diff1 <- unlist(reg.line.diff(X1=NO2.c, Y1=pre.c, X2=NO2.o, Y2=pre.o))
reg.line.diff1

スクリプト内で、ナントカbarは平均、SSナントカは平方和（平均との差の二乗和）や積和（Xの平均との差とYの平均との差の積の和）。

それらを使って、Delta1, Delta2, Delta3を計算している。

Delta1は、傾きが異なるという仮説（対立仮説）のもとでの残差平方和。

Delta2は、傾きは等しいという仮説（帰無仮説）のもとでの残差平方和。

Delta3は、傾きも切片も等しいという仮説の下での残差平方和。

傾きの検定はDelta1とDelta2を使ってF分布で検定する。

F値の分子の自由度は地区の数（2）マイナス 1=1、分母の自由度は、全体のサンプルサイズ（N）マイナス パラメータの数（4つ）。

4つのパラメータとは、Intercept、Slope、地区、Slopeと地区の交互作用（地区ごとにSlopeが異なるという仮説）の4つ。

切片の検定は、Delta2とDelta3を使ってF分布で検定。

F値の分子の自由度は先ほどと同じく地区の数（2）マイナス 1=1、分母の自由度は、N マイナス パラメータの数（3）。

3つのパラメータは、Intercept、Slope、地区の3つ。

結果は、以下の通り。

> reg.line.diff1
Delta1              Delta2            F_Slopes
64.754442586        65.052361246         0.078212660
p_Slopes              Delta3            F_Intcps
0.783108529        96.837793841         8.795034888
p_Intcps              Slope1              Slope2
0.008280926       279.854182655       317.540322581
Intcp1              Intcp2        Slope_Common
-1.489293937         0.110080645       290.976955534
Intcp1_Slope_Common Intcp2_Slope_Common         Diff_Intcps
-1.751184680         0.715725414         2.466910094
Diff_Intcps_LL      Diff_Intcps_UL          Slop_Total
0.719300276         4.214519912       281.451309098
Intcp_Total
-0.355561311

傾きが等しいという帰無仮説は棄却されなかった（p_Slopes ≒ 0.78）ので、同じ傾きにして話を進めてもよいことになる。

共通の傾きは Slope_Common ≒ 290.98 である。

また、傾きが等しい上で、切片が等しいという帰無仮説は棄却された（p_Intcps ≒ 0.0083）ので、切片は異なって、C地区とO地区の回帰直線は並行だが別々がよいということになった。

切片の差は Diff_Intcps ≒ 2.47 で約2.5%だ。

95%信頼区間は0.72％から4.2％（Diff_Intcps_LL ≒ 0.72, Diff_Intcps_UL ≒ 4.21）。

回帰直線の傾きが共通で切片が異なるという結果を回帰直線にして描き入れてみる

結果を図に描き入れてみる。

共通の傾きの線は赤（col=2）で表示している。

C地区は実線で、O地区は点線だ。別々の回帰直線（黒）とほとんど違わないことがわかる。

それならばシンプルなほうがいい。

つまり、NO2濃度と有症割合の関係は地区によって異ならないが、各地区での有症割合レベルが高いか低いかの違いがあるというシンプルなほうがいい。

シンプルなほうが、ほかの地区にも応用が利く可能性が高い。

abline(a=reg.line.diff1[13], b=reg.line.diff1[12], col=2)
abline(a=reg.line.diff1[14], b=reg.line.diff1[12], col=2, lty=2)

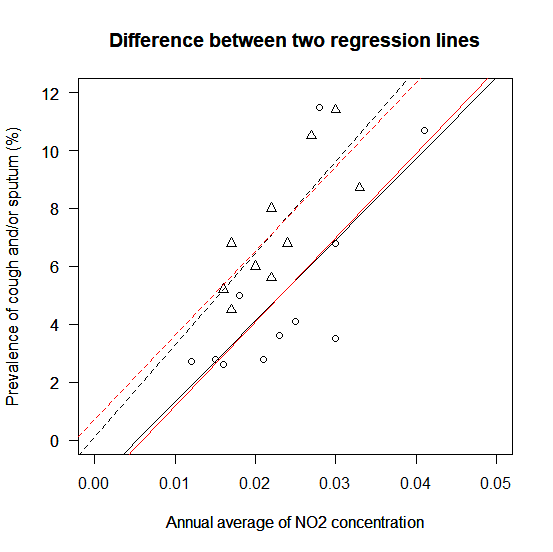
回帰直線の差の検定を lm() で実施してみるとどうなるか

統計ソフトRに組み込まれている関数 lm() を使うとどんなふうにできるか見てみる。

まずデータを少し加工する

dat <- data.frame(NO2=c(NO2.c,NO2.o),pre=c(pre.c,pre.o),are=c(are.c,are.o))

交互作用項を入れたモデル（傾きが別々のモデル）

上記でDelta1を計算したのと同等なのが、交互作用項を入れたモデルになる。

lm1 <- lm(pre~NO2*are, data=dat)
library(car)
Anova(lm1)

Anova()を使うのでcar パッケージをインストールして、使えるようにしておく。

> Anova(lm1)
Anova Table (Type II tests)
Response: pre
Sum Sq Df F value    Pr(>F)
NO2       85.373  1 22.4129 0.0001918 ***
are       31.785  1  8.3446 0.0102038 *
NO2:are    0.298  1  0.0782 0.7831085
Residuals 64.754 17
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

NO2:are が交互作用項。

p値は0.7831085である。

上記の傾きが等しい帰無仮説の検定（p_Slopes=0.783108529）と結果が同じことが確認できる。

ResidualsはDelta1に一致する。

交互作用が有意でないので交互作用項を入れないモデルにする

このモデルが二つの回帰直線の傾きが同じと考えた場合に一致する。

スクリプトは交互作用を外したシンプルなものだ。

lm2 <- lm(pre~NO2+are, data=dat)
summary(lm2)
confint(lm2)
Anova(lm2)

結果は以下の通り。

> summary(lm2)
Call:
lm(formula = pre ~ NO2 + are, data = dat)
Residuals:
Min      1Q  Median      3Q     Max
-3.4781 -1.3413 -0.1781  0.9595  5.1038
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)  -1.7512     1.5217  -1.151 0.264870
NO2         290.9770    59.8680   4.860 0.000126 ***
areo          2.4669     0.8318   2.966 0.008281 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.901 on 18 degrees of freedom
Multiple R-squared:  0.6324,    Adjusted R-squared:  0.5915
F-statistic: 15.48 on 2 and 18 DF,  p-value: 0.0001227

NO2のEstimateが、上記で共通の傾きと称した値（Slope_Common=290.976955534）に一致している。

また、areoのEstimateが上記で言っていた切片の差（Diff_Intcps=2.466910094）に一致している。

InterceptのEstimateと足し合わせると、O地区の切片になる。

InterceptのEstimateはC地区の切片（Intcp1_Slope_Common=-1.751184680）と一致する。

95％信頼区間の結果は以下の通り。

> confint(lm2)
2.5 %     97.5 %
(Intercept)  -4.9481583   1.445789
NO2         165.1990206 416.754891
areo          0.7193003   4.214520

areoの95%信頼区間は、切片の差の信頼区間（Diff_Intcps_LL=0.719300276, Diff_Intcps_UL=4.214519912）に一致する。

このモデルの残差平方和がDelta2=65.052361246と一致しているのがわかる。

> Anova(lm2)
Anova Table (Type II tests)
Response: pre
Sum Sq Df F value    Pr(>F)
NO2       85.373  1  23.623 0.0001257 ***
are       31.785  1   8.795 0.0082809 **
Residuals 65.052 18
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

もし地域差がなければ地域の要因も取り除いて切片も同じと考えてもよい

地域で有意に異なることがわかったのでここで終了だが、もし地域差もない、つまり切片も異ならないのであれば、完全に一つの回帰直線にしてしまってもよい。

lm3 <- lm(pre~NO2, data=dat)
Anova(lm3)

この時の残差平方和がDelta3=96.837793841なのである。

> Anova(lm3)
Anova Table (Type II tests)
Response: pre
Sum Sq Df F value   Pr(>F)
NO2       80.105  1  15.717 0.000831 ***
Residuals 96.838 19
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

まとめ

二つの回帰直線の差の検定を引用書籍に沿って確認してみた。

傾きが異なるかどうかは交互作用項を lm() 内に投入すればよいが、lm()を使わない場合はどうやるか、どんな残差平方和を使って検定するのかが詳細に確認できた。

二つのデータセットがあって、二つの回帰直線が引けたが、さてこの後どうするか？と悩んでしまっている人の次の一手になると思う。

引用書籍

ネタ本は「医学への統計学」6.2.3 二つの母回帰直線の差の検定

最新版はこちら。