医療や疫学研究において、検査値のような連続データを「異常/正常」に区切るカットオフ値の設定は必須である。このカットオフ値を決定する強力な手法がROC曲線分析である。しかし、「ROC分析で最適化したカットオフ値を用いて二値化し、その結果をさらに回帰分析で使う」という一連の手順は、統計学的に見て本当に適切なのであろうか。本記事では、この一般的な手法のメリットとデメリット、そしてより厳密なデータ分析の進め方について、初心者向けに解説する。
カットオフ値を決めるといえばROC曲線分析
医療や研究の分野で、「ある検査の値がどれくらい高ければ病気である(アウトカムがある)と判断すべきか」を決める際、ROC曲線分析(Receiver Operating Characteristic Curve Analysis)が非常によく使われる。
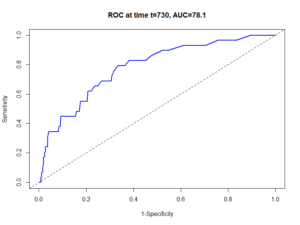
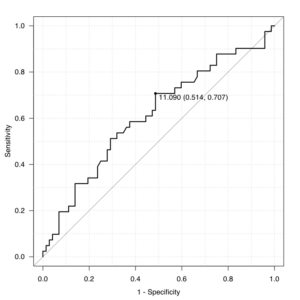
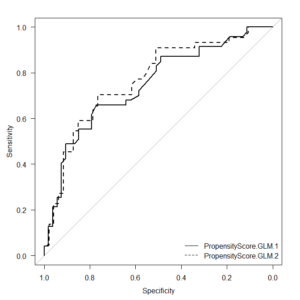
ROC曲線は、検査結果をある値(カットオフ値)で区切ったときの感度(真の陽性率)と特異度(真の陰性率)の関係を図示するもので、この曲線の下の面積(AUC: Area Under the Curve)が大きいほど、その検査がアウトカムを予測する能力が高いとされる。
そして、特定の目的(例えば、「感度を最も高く保ちつつ特異度も確保したい」など)に応じて、感度と特異度のバランスが最も良い点、すなわち「アウトカムを最もよく予測する」と考えられる値が最適なカットオフ値として選ばれる。
連続データのカットオフ値をROC曲線分析で決めて良いか
ROC曲線分析は、検査値のような連続データ(例:血糖値、ホルモン濃度など)を、「陽性/陰性」や「高値/低値」といった二値のカテゴリデータに変換するためのカットオフ値を決定する強力な手法である。
例えば、
- 連続データであるAという検査値を用意する。
- ROC曲線分析を行い、「病気(アウトカム)」の有無を最もよく区別できるAのカットオフ值 $C$ を見つける。
- このカットオフ値 $C$ を用いて、「A $\ge C$ なら高値(陽性)」、「A $< C$ なら低値(陰性)」という二値変数を作る。
- この新しく作った二値変数を説明変数として、アウトカム(例:病気の有無)を予測するロジスティック回帰分析を行う。
このような手順は、特に臨床現場での使いやすさから、頻繁に行われている。
連続データのカットオフ値をROC曲線分析で決めない方が良い理由
しかし、統計学的には、上記の手順、特に「ROC曲線分析で決めたカットオフ値を使って二値化したデータを、同じアウトカムの予測に使う回帰分析」には、いくつかの問題点がある。
1. 情報の損失(Information Loss)
連続データをカットオフ値で二値化すると、本来持っていたデータの詳細な情報が失われる。例えば、カットオフ値を100と設定した場合、検査値が101の人も、200の人も、さらには500の人も、すべて「陽性」と分類される。これにより、101という低リスクの陽性者と、500という高リスクの陽性者の間に存在するリスクの差が無視されてしまう。これは、分析に利用できる情報量を減らしてしまい、統計的な検出力(効果を見つける能力)を低下させる。
2. データドリブンなカットオフ値の利用(Data-Driven Cutoff Bias)
ROC曲線分析は、手持ちのデータセットを最もよく区別できる点を選び出す。この「最も良い点」は、そのデータセットの偶然のノイズや特徴を反映している可能性が高く、他の新しいデータセット(外部検証)に適用した際に、同じように最適な予測力を発揮するとは限らない。これを過剰適合(Overfitting)と呼ぶ。
3. $P$値の歪み(Distortion of $P$-values)
ROC曲線分析でカットオフ値を決め、その結果を使って回帰分析を行うと、分析手順が二重になってしまう。同じデータで「最適な分類」を探し、その結果を「予測力の検定」に使うため、$P$値が実際よりも小さく出やすくなる(統計的に有意になりやすい)という問題が生じる。
連続データのカットオフ値をROC曲線分析で決めるメリットとデメリット
| 項目 | メリット (利点) | デメリット (欠点) |
| 臨床・実務 | ✅ 解釈しやすい: 「この値以上なら危険」と単純化でき、臨床現場や患者への説明が容易である。 | ❌ 情報が失われる: 連続データの詳細な情報(例:数値の増減の度合い)が失われる。 |
| 統計 | ✅ 非線形な関係にも対応: 連続データとして分析すると複雑になる非線形な関係を、単純な二値化で回避できる場合がある。 | ❌ 過剰適合のリスク: 手持ちのデータに最適化しすぎてしまい、他のデータへの汎用性が低くなる。 |
| 実用性 | ✅ ガイドライン作成: 検査や治療の基準として具体的な数値(閾値)を設ける際に必須となる。 | ❌ バイアス(偏り): $P$値が歪み、真の効果よりも大きく見えてしまう可能性がある。 |
どうすればよいのか
統計学的な厳密性と、臨床的な実用性のバランスを考慮すると、以下の方法が推奨される。
1. 連続データをそのまま回帰分析に使う
特別な理由がない限り、予測変数(検査値など)は連続データ(元のスケール)のまま、ロジスティック回帰分析やCox比例ハザードモデルといった回帰分析に投入すべきである。これにより、データの情報損失を防ぎ、より正確なアウトカムの予測(例:検査値が1単位上がるごとにアウトカムのリスクが何倍になるか)が可能になる。
2. カットオフ値は統計的厳密性とは別の目的で利用する
ROC曲線分析でカットオフ値を決めるのは、統計的な予測モデルを構築するためではなく、臨床的なガイドラインやスクリーニング基準を設けるためと割り切るのが賢明である。
推奨されるアプローチ
- 予測モデル構築: 連続データは元のまま回帰分析に使い、正確な予測モデルを作る。
- 臨床判断基準: ROC分析や過去の知見に基づき、現場で「治療介入を開始すべきか」などの判断基準としてカットオフ値を用いる。
3. 外部検証を行う
もしROC分析で決めたカットオフ値を使うなら、その有効性を別の独立したデータセット(外部検証)で検証することが不可欠である。
まとめ
ROC曲線分析は、連続データから最適な二値分類の閾値(カットオフ値)を見つけるための非常に有用なツールである。
しかし、そのカットオフ値を同じデータで決定し、その結果を使って回帰分析を行うと、情報損失や過剰適合といった統計的な問題が生じ、結果の解釈に誤解を招く可能性がある。
最も重要な原則は、「情報は最大限に利用する」ことである。
特別な理由がない限り、連続データは連続データのまま回帰分析に利用し、ROC分析は臨床現場で使いやすい判断基準を設定する目的で利用するのが、統計的にも実用的にもバランスの取れたアプローチである。






コメント