グループごとの平均値が線形の傾向を示しているかどうかを検定する傾向検定をわかりやすく解説
平均値の線形傾向とは
グループごとの平均値の線形傾向とは以下のような状態のことを言う
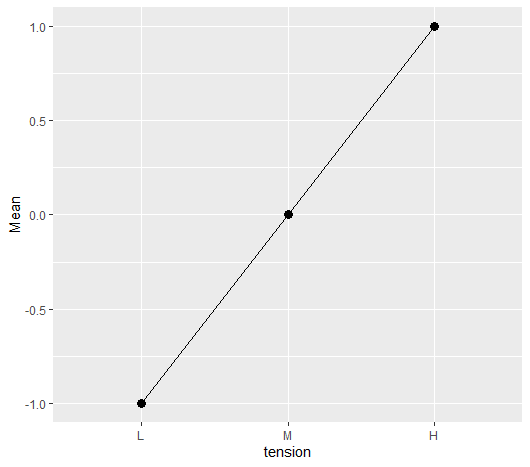
図の中の点は、平均値を表している
平均値を線で結んでいる図である
X 軸の L, M, H という順にだんだんに平均値が高くなっている
X 軸が右に行くに従い、だんだん高くなる、もしくは、だんだん低くなることを線形傾向と呼んでいる
これが統計学的に有意かどうかを検討するものが傾向検定である
平均値の傾向検定を線形対比法で行う方法
各グループの平均値 $ \bar{Y} $ とする
線形傾向を表すスコアのベクトル、これを線形対比係数 $ c $ とする
積の合計を 線形対比 L とすると以下のように書ける
$$ L = \sum c \bar{Y} $$
(添え字は省略している)
一方で、線形対比の分散は、以下のように計算できる
検定を行うには、分散(誤差)が必要なので、分散が登場する
$$ \displaystyle V(L) = \frac{\sigma^{2}}{n} \sum c^{2} $$
n はそれぞれのグループのサンプルサイズ
$ \sigma^2 $ は分散分析の誤差分散(誤差平均平方)である
誤差分散は、こちらも参照
R でトレンド検定の必要サンプルサイズを計算する方法 – 統計ER
このとき検定統計量 T は自由度 N-K の t 分布に従う
$$ \displaystyle T = \frac{\sum c \bar{Y}}{\sqrt{\frac{\sigma^2}{n} \sum c^2}} $$
N は、全グループ合計のサンプルサイズ、K はグループ数である
この検定統計量が大きいときにグループの平均値がだんだんに大きくなる、または、小さくなるという仮説が証明される
傾向検定のカギは平均値と線形対比係数との積和
検定統計量の分子が、線形対比、つまりグループの平均値と線形対比係数の積の和である
線形対比係数のベクトルは、グループの数で決まっている
右肩上がりの線形対比係数を考えると、以下のようになる
- 3 グループ:(-1, 0, 1)
- 4 グループ:(-3, -1, 1, 3)
- 5 グループ:(-2, -1, 0, 1, 2)
線形対比係数の特徴は、合計すると 0 になることと、直線傾向なら等間隔であること
グループの平均値とこれらの線形対比係数の積の和をとるというのは、ベクトルの内積と似ている
ベクトルの内積は、ベクトルがなす角を表現していて、角度が小さく、ベクトルが同じ方向を向いていると最大の 1 に近くなる
線形対比法も、線形対比係数と同じ方向性の場合、その積和(検定統計量の分子)が大きくなり、統計学的有意になるという仕組みになっている
平均値と線形対比係数の図示
平均値と線形対比係数の例を図示してみる
上記とは違い、右肩下がりの例である
平均値のトレンドの図示はこちら
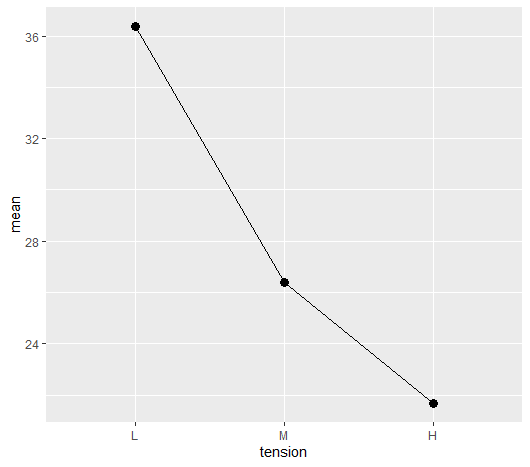
線形対比係数の図示はこちら
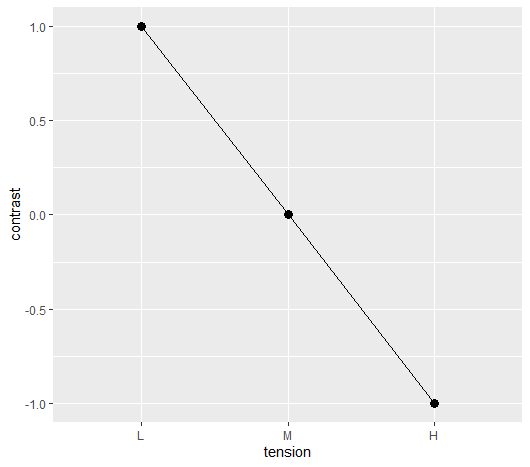
どちらも右肩下がりで下がっていて、同じような方向性である
同じ方向性の場合、これらを掛け合わせた線形対比も大きくなる
結果として検定統計量 T が大きくなり、統計学的有意になる
線形対比係数で設定したように、だんだんに下がる傾向(トレンド)があるということがわかる検定である
平均値の傾向性検定の計算例
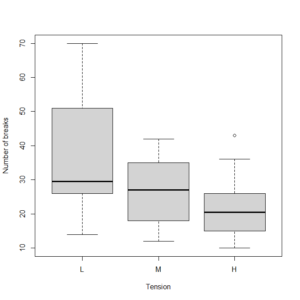
サンプルデータは、R で利用可能なデータで、張力がどのくらいのときに破断が起きるかという毛織物のデータである warpbreaks というデータセットである
tension がどのくらいの時に breaks が起きるのかを平均値と標準偏差を表示した平均値の折れ線グラフで図示すると以下の通りになる
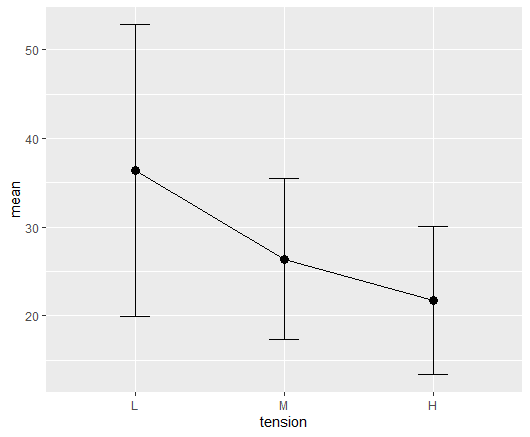
この右下下がりの線形の傾向が統計学的に有意かどうかを、線形対比係数 (1, 0, -1) を用いて検定した結果は以下の通り
> library(dplyr)
>
> # 群ごとの平均値とSD, n を計算
> group.summary <- warpbreaks %>%
+ group_by(tension) %>%
+ summarize(mean=mean(breaks), sd=sd(breaks), n=n())
> group.summary
# A tibble: 3 × 4
tension mean sd n
<fct> <dbl> <dbl> <int>
1 L 36.4 16.4 18
2 M 26.4 9.12 18
3 H 21.7 8.35 18
>
>
> # 線形対比係数の設定
> contrast <- c(1,0,-1)
> contrast
[1] 1 0 -1
>
> # 分散分析
> aov.res <- aov(breaks ~ tension, data=warpbreaks)
> summary(aov.res)
Df Sum Sq Mean Sq F value Pr(>F)
tension 2 2034 1017.1 7.206 0.00175 **
Residuals 51 7199 141.1
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
> # 分散分析表から誤差分散の取り出し
> sigma.sq <- unlist(summary(aov.res))[6]
> sigma.sq
Mean Sq2
141.1481
>
> # K: グループ数
> K <- length(group.summary$tension)
> K
[1] 3
>
> # n: グループのサンプルサイズ
> n <- group.summary$n[1]
> n
[1] 18
>
> # Y.bar: グループごとの平均値
> Y.bar <- unlist(group.summary)[4:6]
> Y.bar
mean1 mean2 mean3
36.38889 26.38889 21.66667
>
> # 検定統計量 T の分子
> Estimate <- sum(contrast*Y.bar)
> Estimate
[1] 14.72222
>
> # 検定統計量 T の分母
> SE <- sqrt(sigma.sq/n * sum(contrast^2))
> SE
Mean Sq2
3.960193
>
> # 検定統計量 T
> T <- Estimate/SE
> names(T) <- 'STATISTIC'
> T
STATISTIC
3.717552
>
> # 有意確率
> PVAL <- pt(T, df=n*3-K, lower.tail = FALSE)*2
> PVAL
STATISTIC
0.0005008605
結果は、p 値が 0.0005 であり、統計学的有意に右肩下がりの傾向が見られたと言える
これは、multcomp パッケージの glht() 関数を使うと、もっと短いスクリプトで計算できる
> library(multcomp)
>
> # 分散分析
> aov.res0 <- aov(breaks ~ tension, data=warpbreaks)
> summary(aov.res0)
Df Sum Sq Mean Sq F value Pr(>F)
tension 2 2034 1017.1 7.206 0.00175 **
Residuals 51 7199 141.1
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
> # 線形対比係数の設定
> contr <- rbind('linear trend' = c(1,0,-1))
> contr
[,1] [,2] [,3]
linear trend 1 0 -1
>
> # 線形対比法による傾向検定
> glht.res <- glht(aov.res0, linfct = mcp(tension = contr))
>
> # 結果表示
> summary(glht.res, test=adjusted('none'))
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: User-defined Contrasts
Fit: aov(formula = breaks ~ tension, data = warpbreaks)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
linear trend == 0 14.72 3.96 3.718 0.000501 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- none method)
p 値は同じ 0.0005 と計算されているのがわかる
まとめ
平均値の傾向性検定について解説した
グループごとの平均値と線形対比係数をかけ合わせた線形対比がカギになる
参考になれば
関連記事









コメント