Rで二元配置分散分析 はどうやるか?
二元配置は、二つの要因があるという意味。
二つの要因があるというのは、例えば、要因Aは3グループにわかれて、各グループごとに要因Bが1から5を持っている、みたいな状態だ。
Step by step でやってみたのと、lm() でパッとやってみた二種類をご紹介。
二元配置分散分析デザインの例
二元配置分散分析の例として例えば、実験であれば、要因Aとして3グループに振り分けて実験A1, A2, A3を行う。
3グループには5人ずついて、5人は、B1からB5までの要因がある(例えば、年齢区分、つまり10代、20代、30代、40代、50代とか)。
実験結果数値に要因Aと要因Bは要因内グループ間で違いがあるか、つまり関連しているかを見ることができる。
Rで二元配置分散分析を行うにあたり使用するデータ
記事最下段の参考書籍 例題8.5のデータを使う。
以下の通り。A1, A2, A3と縦ベクトル(上からB1~B5の5つのデータ)で入力して、要因Aと要因Bの番号をつける。
A1 <- c(9.48,9.52,9.32,9.98,10.00)
A2 <- c(9.24,9.95,9.20,9.68,9.94)
A3 <- c(8.66,8.50,8.76,9.11,9.75)
B <- factor(c(rep(1:5,3)))
A <- factor(sort(c(rep(1:3,5))))
X <- c(A1,A2,A3)
data.frame(X,A,B)
出来上がりは、こんな構造になる。
> data.frame(X,A,B)
X A B
1 9.48 1 1
2 9.52 1 2
3 9.32 1 3
4 9.98 1 4
5 10.00 1 5
6 9.24 2 1
7 9.95 2 2
8 9.20 2 3
9 9.68 2 4
10 9.94 2 5
11 8.66 3 1
12 8.50 3 2
13 8.76 3 3
14 9.11 3 4
15 9.75 3 5
Rで二元配置分散分析の計算をStep by step で行う方法
二元配置分散分析を一歩ずつスクリプトにしてみると以下のようになる。
two.way.anova <- function(X,A,B){
Xbar <- mean(X)
Xjbar <- tapply(X, A, mean)
Xibar <- tapply(X, B, mean)
b <- length(table(B))
a <- length(table(A))
N <- length(X)
SS <- sum((X-Xbar)^2)
SSA <- b*sum((Xjbar-Xbar)^2)
SSB <- a*sum((Xibar-Xbar)^2)
SSE <- SS-SSA-SSB
nu <- N-1
nuA <- a-1
nuB <- b-1
nuE <- (a-1)*(b-1)
VA <- SSA/nuA
VB <- SSB/nuB
VE <- SSE/nuE
FA <- VA/VE
FB <- VB/VE
pFA <- pf(FA, nuA, nuE, lower.tail=FALSE)
pFB <- pf(FB, nuB, nuE, lower.tail=FALSE)
list(c(SS_A=SSA, nu_A=nuA, V_A=VA, F_A=FA, p_FA=pFA,
SS_B=SSB, nu_B=nuB, V_B=VB, F_B=FB, p_FB=pFB,
SS_E=SSE, nu_E=nuE, V_E=VE, SS=SS, nu=nu))
}
two.way.anova1 <- unlist(two.way.anova(X=X, A=A, B=B))
two.way.anova1
全体平均(Xbar)、要因Aの平均(Xjbar)、要因Bの平均(Xibar)を算出する。
次に、全体のサンプルサイズ(N)、要因Aのグループ数(a)、要因Bのグループ数(b)を求める。
そして、平方和の計算をする。
全体の平方和(SS)、要因Aの平方和(SSA)、要因Bの平方和(SSB)、残差平方和(SSE)を計算する。
さらに、それぞれの平方和の自由度を計算する。
全体(N-1)、要因A(nuA)、要因B(nuB)、残差(nuE)の自由度を計算する。
平方和を自由度で割って、平均平方和を計算する。
要因Aの平均平方和がVA、要因Bの平均平方和がVB、残差の平均平方和がVE。
VAとVEの比が要因AのF値(FA)。
VBとVEの比が要因BのF値(FB)。
F値がとても大きければ統計学的に有意(p値が小さくなる)で、要因が意味があるという結果になる。
つまり要因Aのグループ間の平均に差がある。
要因Bのグループ間の平均に差がある。
という結果になる。
結果はこちら。
> two.way.anova1
SS_A nu_A V_A F_A p_FA
1.527160000 2.000000000 0.763580000 11.394448866 0.004558095
SS_B nu_B V_B F_B p_FB
1.371693333 4.000000000 0.342923333 5.117240350 0.024168724
SS_E nu_E V_E SS nu
0.536106667 8.000000000 0.067013333 3.434960000 14.000000000
要因AのF値は11.39、p値は0.004558で統計学的有意。
要因BのF値は5.12、p値は0.024169でこちらも統計学的に有意。
つまり、要因Aのグループ間も要因Bのグループ間も統計学的に意味のある差があると言える。
要因Aと要因Bの各グループ間の平均値を示すと以下の通り。
要因AはA3だけ異なるように見える。
また要因Bは、B2,B4が中間で、B1とB3が低くて、B5が高いように見える。
> tapply(X, A, mean)
1 2 3
9.660 9.602 8.956
> tapply(X, B, mean)
1 2 3 4 5
9.126667 9.323333 9.093333 9.590000 9.896667
Rで二元配置分散分析を行うのに lm() を使う方法
lm() を使えばあっという間だ。
AとBをプラスでつなぐ。
Xを予測するモデルとして投入する。
car パッケージを使うので先にインストールしておく。
install.packages('car')
lm で計算して、Anova で分散分析の結果を出力する。
lm1 <- lm(X ~ A+B)
library(car)
Anova(lm1)
結果はこちら。
> Anova(lm1)
Anova Table (Type II tests)
Response: X
Sum Sq Df F value Pr(>F)
A 1.52716 2 11.3944 0.004558 **
B 1.37169 4 5.1172 0.024169 *
Residuals 0.53611 8
A の Sum Sq(Sum of Square)が上記の SSA と一致していて、B の Sum Sqが SSB と一致している。
p値も上記の計算と一致している。
Residuals の Sum SqはSSEと同じだ。
Rで二元配置分散分析を行列計算で実施する
行列で計算するためのデータの準備
デザイン行列なるものを作る。
要因Aは三グループある。
これを0と1で、2つの変数で表すとすれば、要因Aが1のときに(0,0)、要因Aが2の時に(1,0)、要因Aが3の時に(0,1)となる2つの変数A2とA3を作る。
これをダミー変数と呼ぶ。
要因Bは五グループ。
こちらも一つ少ない四つの変数で表す。
B2, B3, B4, B5だ。
切片(Intercept)として、ぜんぶ1のベクトルを結合する。
測定値はyに名前を変えて、サンプルサイズはN、推定するパラメータの数をpとする。
N <- length(X)
A2 <- c(rep(0,5),rep(1,5),rep(0,5))
A3 <- c(rep(0,10),rep(1,5))
A.mat <- data.frame(A2,A3)
B.mat0 <- rbind(rep(0,4),diag(1,nr=4,nc=4))
B.mat <- rbind(B.mat0,B.mat0,B.mat0)
colnames(B.mat) <- paste("B",2:5,sep="")
X.mat0 <- data.frame("Intercept"=rep(1,N),A.mat,B.mat)
y <- X
(X.mat <- as.matrix(X.mat0))
p <- length(X.mat0)
デザイン行列の出来上がりは以下のとおり。
> (X.mat <- as.matrix(X.mat0))
Intercept A2 A3 B2 B3 B4 B5
[1,] 1 0 0 0 0 0 0
[2,] 1 0 0 1 0 0 0
[3,] 1 0 0 0 1 0 0
[4,] 1 0 0 0 0 1 0
[5,] 1 0 0 0 0 0 1
[6,] 1 1 0 0 0 0 0
[7,] 1 1 0 1 0 0 0
[8,] 1 1 0 0 1 0 0
[9,] 1 1 0 0 0 1 0
[10,] 1 1 0 0 0 0 1
[11,] 1 0 1 0 0 0 0
[12,] 1 0 1 1 0 0 0
[13,] 1 0 1 0 1 0 0
[14,] 1 0 1 0 0 1 0
[15,] 1 0 1 0 0 0 1
要因A及びBの各グループの効果
要因AとBの各グループの効果は以下の行列式で計算できる。
いわゆる最小二乗法を行列で行う方法だ。
これはlm()のcoefficientsで出力されるEstimateに一致する。
(theta.hat <- solve(t(X.mat)%*%X.mat)%*%t(X.mat)%*%y)
summary(lm1)$coefficients
結果は以下の通り。
> (theta.hat <- solve(t(X.mat)%*%X.mat)%*%t(X.mat)%*%y)
[,1]
Intercept 9.38066667
A2 -0.05800000
A3 -0.70400000
B2 0.19666667
B3 -0.03333333
B4 0.46333333
B5 0.77000000
> summary(lm1)$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.38066667 0.1768414 53.0456412 1.768404e-11
A2 -0.05800000 0.1637233 -0.3542561 7.323031e-01
A3 -0.70400000 0.1637233 -4.2999366 2.615979e-03
B2 0.19666667 0.2113659 0.9304559 3.793567e-01
B3 -0.03333333 0.2113659 -0.1577044 8.785976e-01
B4 0.46333333 0.2113659 2.1920909 5.972596e-02
B5 0.77000000 0.2113659 3.6429713 6.560704e-03
行列による最小二乗法の計算 step by step はこちらを参照。
予測値の計算
誤差分散(sigma2)のために予測値(y.hat)が必要になる。
以下のようにしてy.hatを計算する。
これは、lm()の結果を使って、preict()で予測値を出力させた結果に一致する。
(y.hat <- X.mat%*%theta.hat)
as.matrix(predict(lm1))
plot(y.hat, y)
abline(a=0,b=1)
出力結果は以下の通り。
> (y.hat <- X.mat%*%theta.hat)
[,1]
[1,] 9.380667
[2,] 9.577333
[3,] 9.347333
[4,] 9.844000
[5,] 10.150667
[6,] 9.322667
[7,] 9.519333
[8,] 9.289333
[9,] 9.786000
[10,] 10.092667
[11,] 8.676667
[12,] 8.873333
[13,] 8.643333
[14,] 9.140000
[15,] 9.446667
> as.matrix(predict(lm1))
[,1]
1 9.380667
2 9.577333
3 9.347333
4 9.844000
5 10.150667
6 9.322667
7 9.519333
8 9.289333
9 9.786000
10 10.092667
11 8.676667
12 8.873333
13 8.643333
14 9.140000
15 9.446667
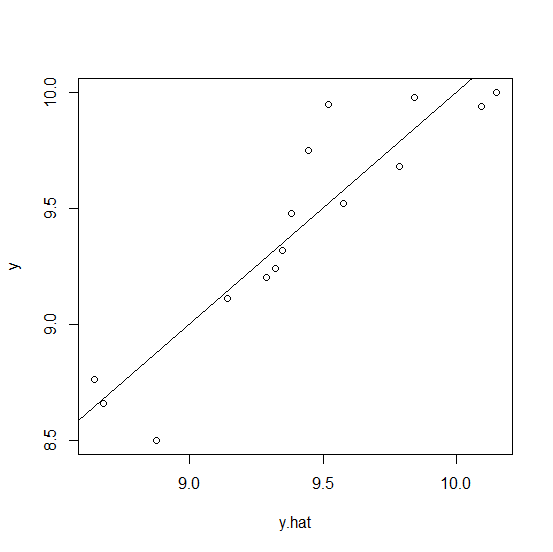
実測値yと予測値y.hatの散布図とy=xの直線(つまり完全一致)を描き入れた図は以下の通り。
一致というには無理がある散布図だ。
要因Aと要因Bだけでは完全には説明できないわけだ。
各グループの効果の検定
残差平方和(SSE)を計算し、誤差分散(sigma2)を計算し、分散共分散行列を計算して、最後にパラメータの標準誤差を計算する。
パラメータと標準誤差の比がt値であり、自由度N-pのt分布に従うことを使って仮説検定を行う。
(SSE <- sum((y-y.hat)^2))
sigma2 <- SSE/(N-p)
V.theta <- sigma2*solve(t(X.mat)%*%X.mat)
(SE.theta <- as.matrix(sqrt(diag(V.theta))))
t <- theta.hat/SE.theta
2*pt(abs(t), N-p, lower.tail=FALSE)
標準誤差もp値も確認してみれば、summary(lm1)$coefficients で出力される結果と一致しているのがわかる。
> (SSE <- sum((y-y.hat)^2))
[1] 0.5361067
> (SE.theta <- as.matrix(sqrt(diag(V.theta))))
[,1]
Intercept 0.1768414
A2 0.1637233
A3 0.1637233
B2 0.2113659
B3 0.2113659
B4 0.2113659
B5 0.2113659
> 2*pt(abs(t), N-p, lower.tail=FALSE)
[,1]
Intercept 1.768404e-11
A2 7.323031e-01
A3 2.615979e-03
B2 3.793567e-01
B3 8.785976e-01
B4 5.972596e-02
B5 6.560704e-03
> summary(lm1)$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.38066667 0.1768414 53.0456412 1.768404e-11
A2 -0.05800000 0.1637233 -0.3542561 7.323031e-01
A3 -0.70400000 0.1637233 -4.2999366 2.615979e-03
B2 0.19666667 0.2113659 0.9304559 3.793567e-01
B3 -0.03333333 0.2113659 -0.1577044 8.785976e-01
B4 0.46333333 0.2113659 2.1920909 5.972596e-02
B5 0.77000000 0.2113659 3.6429713 6.560704e-03
要因Aの検定
要因Aが意味があるかどうかの検定は、要因Aをデザイン行列から削除した計算結果を使って検討できる。
要因Aを削除したデザイン行列で計算した予測値から計算した残差平方和(SSE.A)を使って、F値を計算し、F分布で検定する。
SSE.AとSSEの差が大きければF値が大きくなる。
その場合は要因Aを削除した影響が大きいと考える。
つまり、要因Aは重要な要因で外せないと判断するわけだ。
(X.mat1 <- as.matrix(data.frame("Intercept"=rep(1,N),B.mat)))
a <- length(table(A))
theta.hat1 <- solve(t(X.mat1)%*%X.mat1)%*%t(X.mat1)%*%y
y.hat1 <- X.mat1%*%theta.hat1
SSE.A <- sum((y-y.hat1)^2)
SSE.A-SSE
(FA <- ((SSE.A-SSE)/(a-1))/(SSE/(N-p)))
(pFA <- pf(FA, a-1, N-p, lower.tail=FALSE))
two.way.anova1
Anova(lm1)
要因Aを除いたデザイン行列は以下のようになる。
> (X.mat1 <- as.matrix(data.frame("Intercept"=rep(1,N),B.mat)))
Intercept B2 B3 B4 B5
[1,] 1 0 0 0 0
[2,] 1 1 0 0 0
[3,] 1 0 1 0 0
[4,] 1 0 0 1 0
[5,] 1 0 0 0 1
[6,] 1 0 0 0 0
[7,] 1 1 0 0 0
[8,] 1 0 1 0 0
[9,] 1 0 0 1 0
[10,] 1 0 0 0 1
[11,] 1 0 0 0 0
[12,] 1 1 0 0 0
[13,] 1 0 1 0 0
[14,] 1 0 0 1 0
[15,] 1 0 0 0 1
結果は以下の通り。
> SSE.A-SSE
[1] 1.52716
> (FA <- ((SSE.A-SSE)/(a-1))/(SSE/(N-p)))
[1] 11.39445
> (pFA <- pf(FA, a-1, N-p, lower.tail=FALSE))
[1] 0.004558095
> two.way.anova1
SS_A nu_A V_A F_A p_FA
1.527160000 2.000000000 0.763580000 11.394448866 0.004558095
SS_B nu_B V_B F_B p_FB
1.371693333 4.000000000 0.342923333 5.117240350 0.024168724
SS_E nu_E V_E SS nu
0.536106667 8.000000000 0.067013333 3.434960000 14.000000000
> Anova(lm1)
Anova Table (Type II tests)
Response: X
Sum Sq Df F value Pr(>F)
A 1.52716 2 11.3944 0.004558 **
B 1.37169 4 5.1172 0.024169 *
Residuals 0.53611 8
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
SSE.A-SSEは、SS_Aに一致しているのがわかる。
つまり要因Aの平方和ということだ。
FA、pFAも行列を使わない計算と同値だ。
Anova()の結果A行の、Sum SqとF value 、Pr(>F)にそれぞれ一致している。
要因Bの検定
同様に、要因Bの検定は要因Bを除いた残差平方和(SSE.B)を計算する。
そのために要因Bを除いたデザイン行列を作る。
結果も同様で、SSE.B-SSEはSS_Bに一致する。
FB、pFBは、行列を使わない結果F_B、p_FBに一致し、Anova()の結果B行のSum Sq、F value 、Pr(>F)と一致している。
(X.mat2 <- as.matrix(data.frame("Intercept"=rep(1,N),A.mat)))
b <- length(table(B))
theta.hat2 <- solve(t(X.mat2)%*%X.mat2)%*%t(X.mat2)%*%y
y.hat2 <- X.mat2%*%theta.hat2
SSE.B <- sum((y-y.hat2)^2)
SSE.B-SSE
(FB <- ((SSE.B-SSE)/(b-1))/(SSE/(N-p)))
(pFB <- pf(FB, b-1, N-p, lower.tail=FALSE))
デザイン行列はこちら。
> (X.mat2 <- as.matrix(data.frame("Intercept"=rep(1,N),A.mat)))
Intercept A2 A3
[1,] 1 0 0
[2,] 1 0 0
[3,] 1 0 0
[4,] 1 0 0
[5,] 1 0 0
[6,] 1 1 0
[7,] 1 1 0
[8,] 1 1 0
[9,] 1 1 0
[10,] 1 1 0
[11,] 1 0 1
[12,] 1 0 1
[13,] 1 0 1
[14,] 1 0 1
[15,] 1 0 1
残差平方和とF値、p値の結果は以下の通り。
> SSE.B-SSE
[1] 1.371693
> (FB <- ((SSE.B-SSE)/(b-1))/(SSE/(N-p)))
[1] 5.11724
> (pFB <- pf(FB, b-1, N-p, lower.tail=FALSE))
[1] 0.02416872
まとめ
二元配置分散分析は一見するととても難しそうだが、一歩一歩確認していくと、それほどでもないことがわかる。
二元配置分散分析を、行列式を使った計算方法でも実施してみた。
行列を使わない方法とやり方が大きく異なるが、結果が一致するのがとても面白い。
一度腰を据えて、step by stepでやってみる価値はある。
参考書籍
教科書は「医学への統計学」8.3.1 二元配置分散分析

最新版はこちら。










コメント