二元配置分散分析で交互作用があるデータを R で分析する方法。
二元配置分散分析 交互作用がある場合の方法 サンプルデータ
二元配置分散分析で交互作用がある場合の解析を行うためのサンプルデータは carData パッケージの Moore データセットを用いる。
carData パッケージは car パッケージをインストールすると一緒にインストールされる。
インストール方法がわからない場合はこちらから確認。

Moore データは、パートナーがうその否定をしていることにどれだけ従うかを見た心理実験の結果。
パートナーのステータスが高い・低いと、権威主義かどうか(Authoritarianism、低い、中程度、高いに三分割してfcategoryとしている)で、うそに従ってしまう数(conformity)がどれくらいかを実験している。
car パッケージを呼び出して、lm() と Anova() を使って解析する場合、以下のようなスクリプトで解析できる。
library(car)
mod <- lm(conformity ~ fcategory*partner.status, data=Moore)
summary(mod)
Anova(mod)
結果は以下の通り。
> summary(mod)
Call:
lm(formula = conformity ~ fcategory * partner.status, data = Moore)
Residuals:
Min 1Q Median 3Q Max
-8.6250 -2.9000 -0.2727 2.7273 11.3750
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.8571 1.7307 6.851 3.44e-08 ***
fcategorylow 5.5429 2.6813 2.067 0.0454 *
fcategorymedium 2.4156 2.2140 1.091 0.2819
partner.statuslow 0.7679 2.3699 0.324 0.7477
fcategorylow:partner.statuslow -9.2679 3.4507 -2.686 0.0106 *
fcategorymedium:partner.statuslow -7.7906 3.5728 -2.181 0.0353 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.579 on 39 degrees of freedom
Multiple R-squared: 0.3237, Adjusted R-squared: 0.237
F-statistic: 3.734 on 5 and 39 DF, p-value: 0.007397
> Anova(mod)
Anova Table (Type II tests)
Response: conformity
Sum Sq Df F value Pr(>F)
fcategory 11.61 2 0.2770 0.759564
partner.status 212.21 1 10.1207 0.002874 **
fcategory:partner.status 175.49 2 4.1846 0.022572 *
Residuals 817.76 39
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
交互作用はp=0.022572で、統計学的有意。
交互作用があるということは、パートナーステータスもしくは権威主義のどちらかで層別に解析するなど対策を行わないといけない。
二元配置分散分析で交互作用がある場合の平均値を図示してみる
それではまず、データをグラフにしてみる。
パートナーのステータスと権威主義別に平均値を算出してグラフにしてみる。
means <- tapply(Moore$conformity, list(Moore$partner.status,Moore$fcategory), mean)
(means1 <- means[c(2,1),c(2,3,1)])
matplot(t(means1),type="b",
ylab="Mean of conformity",xlab="Authoritarianism",
las=1,xaxt="n")
axis(side=1,at=1:3,label=c("Low","Middle","High"))
legend("topright",c("Low","High"),lty=1:2,col=1:2)
title("Conformity by Partner's Status")
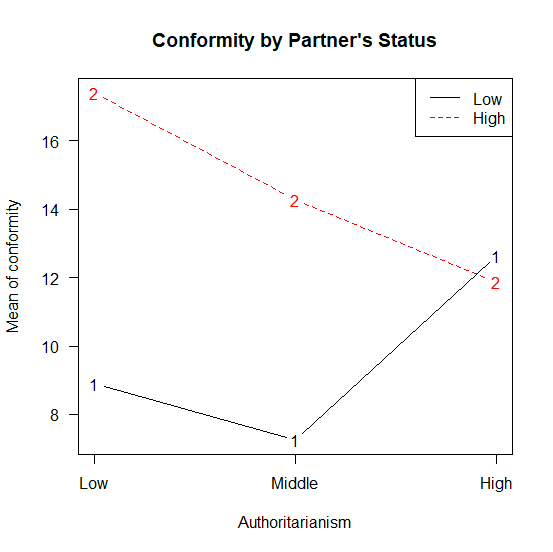
平均値は以下の通り。
> (means1 <- means[c(2,1),c(2,3,1)])
low medium high
low 8.9 7.25000 12.62500
high 17.4 14.27273 11.85714
グラフにすると明らかにパートナーのステータスで傾向が違うのが見て取れる。
パートナーのステータスが低い場合、権威主義が高くなるにしたがって、従う(Conformtity)回数が増える。
しかし、パートナーのステータスが高い場合は、権威主義が低い人ほど、うそに従ってしまう。
これはとても興味深い。
権威主義に反対しているのに、ステータスが高い人には従ってしまうという、行っていることと行動が矛盾しているわけだ。
二元配置分散分析のために交互作用項を作成してデザイン行列を作る
二元配置分散分析の実際の計算に入っていく。
まず、fcategoryやpartner.statusをダミー変数に変換し、デザイン行列を作る。
分散分析ではこれが最初のステップ。
Moore1 <- Moore
Moore1$fcat.low <- ifelse(Moore$fcategory=="low", 1, 0)
Moore1$fcat.med <- ifelse(Moore$fcategory=="medium", 1, 0)
Moore1$part.low <- ifelse(Moore$partner.status=="low", 1, 0)
Moore1$low.low <- Moore1$fcat.low * Moore1$part.low
Moore1$med.low <- Moore1$fcat.med * Moore1$part.low
X.mat0 <- data.frame("Intercept"=rep(1,45),Moore1[,5:9])
p <- length(X.mat0)
y <- Moore1[,2]
(X.mat1 <- as.matrix(X.mat0))
N <- length(y)
作成したデザイン行列は、以下のとおり。これがキモになって、各要因の水準別平均値が計算される。low.lowとかmed.lowが交互作用項だ。
> (X.mat1 <- as.matrix(X.mat0))
Intercept fcat.low fcat.med part.low low.low med.low
1 1 1 0 1 1 0
2 1 0 0 1 0 0
3 1 0 0 1 0 0
4 1 1 0 1 1 0
5 1 1 0 1 1 0
6 1 1 0 1 1 0
7 1 0 1 1 0 1
8 1 0 1 1 0 1
9 1 1 0 1 1 0
10 1 1 0 1 1 0
11 1 0 1 1 0 1
12 1 0 0 1 0 0
13 1 1 0 1 1 0
14 1 0 1 1 0 1
15 1 0 0 1 0 0
16 1 0 0 1 0 0
17 1 1 0 1 1 0
18 1 0 0 1 0 0
19 1 0 0 1 0 0
20 1 0 0 1 0 0
21 1 1 0 1 1 0
22 1 1 0 1 1 0
23 1 0 0 0 0 0
24 1 0 1 0 0 0
25 1 1 0 0 0 0
26 1 0 0 0 0 0
27 1 1 0 0 0 0
28 1 0 0 0 0 0
29 1 0 1 0 0 0
30 1 0 1 0 0 0
31 1 0 0 0 0 0
32 1 0 1 0 0 0
33 1 1 0 0 0 0
34 1 0 1 0 0 0
35 1 0 1 0 0 0
36 1 1 0 0 0 0
37 1 0 0 0 0 0
38 1 0 1 0 0 0
39 1 0 1 0 0 0
40 1 0 1 0 0 0
41 1 0 1 0 0 0
42 1 0 0 0 0 0
43 1 1 0 0 0 0
44 1 0 0 0 0 0
45 1 0 1 0 0 0
二元配置分散分析の推定値・標準誤差・t値・p値
次に、推定値、標準誤差、t値、p値の計算に移る。
推定値は theta というベクトルに計算結果が入るようにしている。
推定値とデザイン行列を使ってy(conformity)の予測値(y.hat)を計算する。
y と y.hat で誤差平方和(SSE)を計算する。
誤差分散を計算し、標準誤差(SE)を計算する。
theta と SE の比が t 値であり、サンプルサイズ-パラメータ数(N-p)を自由度として p 値を計算する。
theta <- solve(t(X.mat1)%*%(X.mat1))%*%t(X.mat1)%*%y
y.hat <- X.mat1%*%theta
SSE <- sum((y-y.hat)^2)
sigma2 <- SSE/(N-p)
SE <- sqrt(diag(sigma2*solve(t(X.mat1)%*%(X.mat1))))
matrix(SE)
t <- theta/SE
matrix(t)
2*pt(abs(t), N-p, lower.tail=FALSE)
summary(mod)$coefficients
結果は以下の通り。
標準誤差(SE)、t値、p値が summary()$coefficients の結果と一致していることが見て取れる。
> matrix(SE)
[,1]
[1,] 1.730743
[2,] 2.681256
[3,] 2.213974
[4,] 2.369918
[5,] 3.450653
[6,] 3.572786
> matrix(t)
[,1]
[1,] 6.8508963
[2,] 2.0672614
[3,] 1.0910625
[4,] 0.3240016
[5,] -2.6858274
[6,] -2.1805351
> 2*pt(abs(t), N-p, lower.tail=FALSE)
[,1]
Intercept 3.435671e-08
fcat.low 4.539152e-02
fcat.med 2.819404e-01
part.low 7.476681e-01
low.low 1.057284e-02
med.low 3.531472e-02
> summary(mod)$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.8571429 1.730743 6.8508963 3.435671e-08
fcategorylow 5.5428571 2.681256 2.0672614 4.539152e-02
fcategorymedium 2.4155844 2.213974 1.0910625 2.819404e-01
partner.statuslow 0.7678571 2.369918 0.3240016 7.476681e-01
fcategorylow:partner.statuslow -9.2678571 3.450653 -2.6858274 1.057284e-02
fcategorymedium:partner.statuslow -7.7905844 3.572786 -2.1805351 3.531472e-02
二元配置分散分析の交互作用項の有意性の検定
最後に、交互作用項が有意であるかどうかの検定の方法について。
これは交互作用項を含まないモデル(デザイン行列)を作成して、そこから得られる予測値とその予測値を使った残差平方和を使って F 分布に従う F 値を計算する。
X.mat02 <- data.frame("Intercept"=rep(1,45),Moore1[,5:7])
p2 <- length(X.mat02)
X.mat2 <- as.matrix(X.mat02)
theta2 <- solve(t(X.mat2)%*%(X.mat2))%*%t(X.mat2)%*%y
y.hat2 <- X.mat2%*%theta2
SSE2 <- sum((y-y.hat2)^2)
F <- (SSE2-SSE)/((length(table(Moore1$fcategory))-1)*(length(table(Moore1$partner.status))-1))/(SSE/(N-p))
pf(F, (length(table(Moore1$fcategory))-1)*(length(table(Moore1$partner.status))-1), N-p, lower.tail=FALSE)
Anova(mod)
最終的な p 値は以下の通り。
これは Anova() で計算した時の交互作用項の p 値に一致している。
> pf(F, (length(table(Moore1$fcategory))-1)*(length(table(Moore1$partner.status))-1), N-p, lower.tail=FALSE)
[1] 0.02257244
ちなみに交互作用は、二つの要因それぞれのカテゴリ-1を掛け算した数がパラメータとしてデザイン行列に投影されている。
たとえば、今回の場合は fcategory が High, Medium, Low の三つなので 3-1=2、partner.status が High と Low の二つなので2-1=1、つまり 2×1=2 ということで、二つの交互作用項 low.low と med.low があった(自由度 2 )。
この結果は Anova() の結果中の fcategory:partner.status の項の Pr(>F) と一致する。
> Anova(mod)
Anova Table (Type II tests)
Response: conformity
Sum Sq Df F value Pr(>F)
fcategory 11.61 2 0.2770 0.759564
partner.status 212.21 1 10.1207 0.002874 **
fcategory:partner.status 175.49 2 4.1846 0.022572 *
Residuals 817.76 39
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
まとめ
二元配置分散分析で交互作用項を含めた解析を行ってみた。
Step by step でデザイン行列を作るところからやってみると、実際にどんな計算をしているか手に取るようにわかる。
関連記事
二元に配置分散分析で交互作用がない場合の方法は以下を参照。








コメント